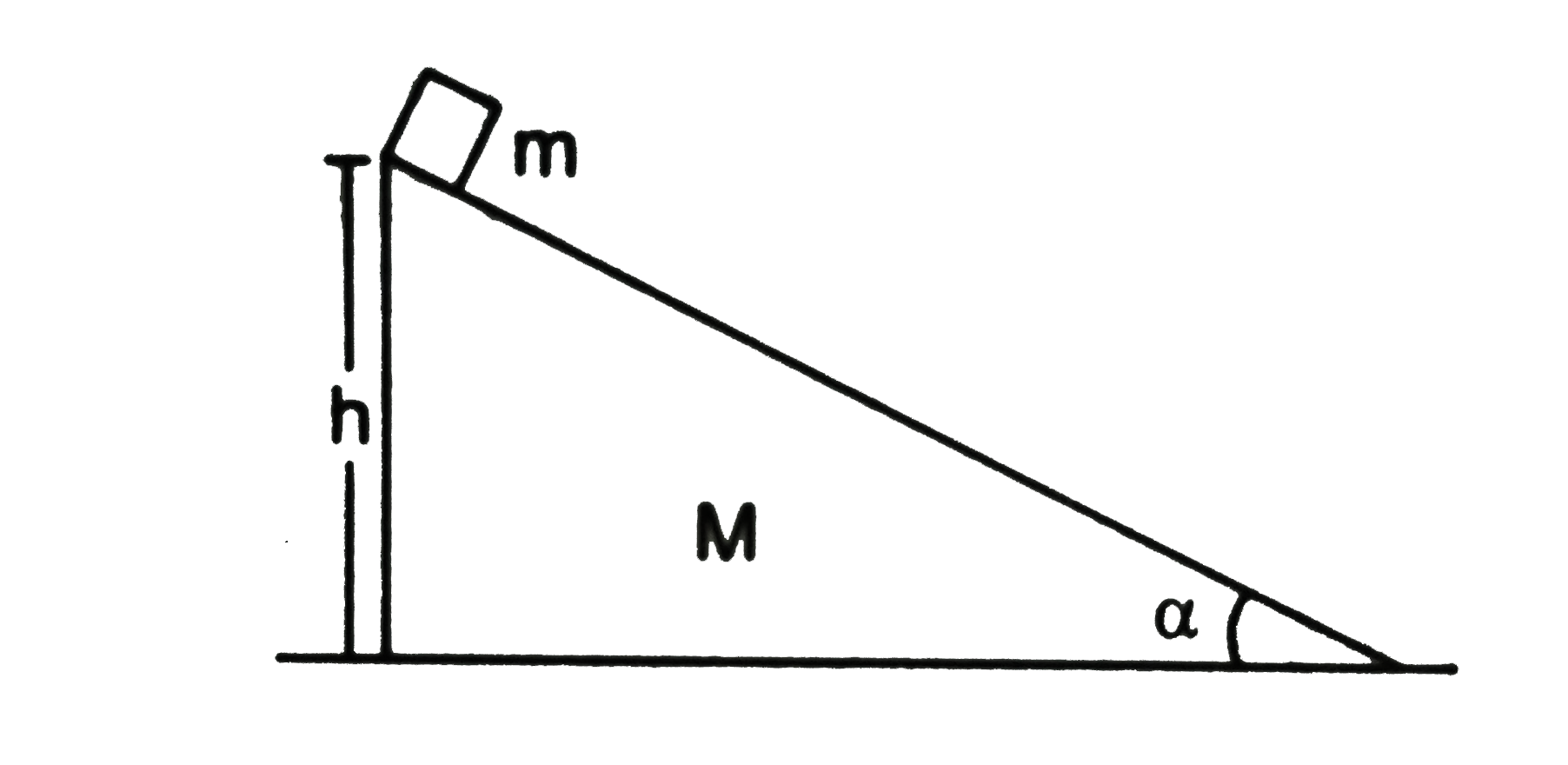
A block of mas m is placed on a triangular block of mas m, which in tunis placed on a horizontal surface as shown in figure. Assuming frictionless surfaces find the velocity of the triangular block when the smaller block reaches the bottom end.
The correct Answer is:A, B, C
The block m will slide down the inclined pklane of mass M with aceleration a1=gsinα (relative) to the inclined plane.
The horizontal component of a1 will be ax=gsinαcosα,forwhichtheblcokMwillae≤rate→wards≤ft,≤ttehae≤rationbea_2.<br>Aord∈g→theconceptofcentreofmass,(∈thehorizontldirecrtionexterNAlforceiszero)<br>ma_x=(M+m)a_2<br>rarr a_2=(ma_x)/(M+m)<br>=(mgsiN/Alpha cosalpha)/(M+m)......i<br>>sothe|o|lute(ress–tant)ae≤rationofmontheblockMalongthedirectionofthe∈cl∈ewillbe<br>a=gsiN/Alpha-a_2cosalpha<br>=gsiN/Alpha- (mgsiN/Alphacos^2alpha)/(M+m)<br>=gsiN/Alpha[1-(mcos^2alpha)/(M+m)]<br>=g sin alpha[(M+m-mcos^2alpha)/(M+m)]<br>So,a=g siN/Alpha [(M+msin^2alpha)/(M+m)]...ii<br>Letthetimetakenbytheblockm→reachthe⊥→mendbet<br>Now, S=ut+(1/2)at^2<br>rarrh/(siN/Alpha)=(1/2)at^2<br>rarr t=(sqrt(2h)/(a siN/Alpha))<br>So,thevelocityofthebig≥rblockaftertimetwillbe<br>v_m=u=a_2t<br>=(mgsiN/Alphacosalpha)/(M+m)<br>⎛⎝√2hαsiNAlpha⎞⎠
=⎡⎣2m2g2hsin2αcos2α(M+m)2asiNAlpha⎤⎦12
now substituting the value of a from equtioin ii we get
Vm=⎡⎣2m2g2hsin2α(M+m)2siNAlpha×cos2αgsiNAlpha(M+m)(M+msin2α)⎤⎦
or Vm=⎡⎢⎣2m2ghcos2α((M+m)(M+msin2α)]12
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMACHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Objective 2
11 Videos
- CALORIMETRYBOOK - HC VERMACHAPTER - CALORIMETRYEXERCISE - Exercises
18 Videos
- CIRCULAR MOTIONBOOK - HC VERMACHAPTER - CIRCULAR MOTIONEXERCISE - Exercises
30 Videos
Similar Questions
A block of mass m is placed on a triangular block of mass M(M=2m) , as shown. All surfaces are smooth. Calculate the velocity of triangular block when the smaller block reaches at bottom.

View SolutionFigure shows a small block of mass m which is started with a speed v on the horizontal part of the bigger block of mas m placed on a horizontal floor. The curved part of the surface shown is semicircular. All the surfaces are frictionless. Find the speed of the bigger block when the smaller block reaches the point A of the surface.

View Solution
Knowledge Check
A block of mass M is placed on the top of a bigger block of mass 10 M as shown in figure. All the surfaces are frictionless. The system is released from rest, then the distance moved by the bigger block at the instant the smaller block reaches the ground :
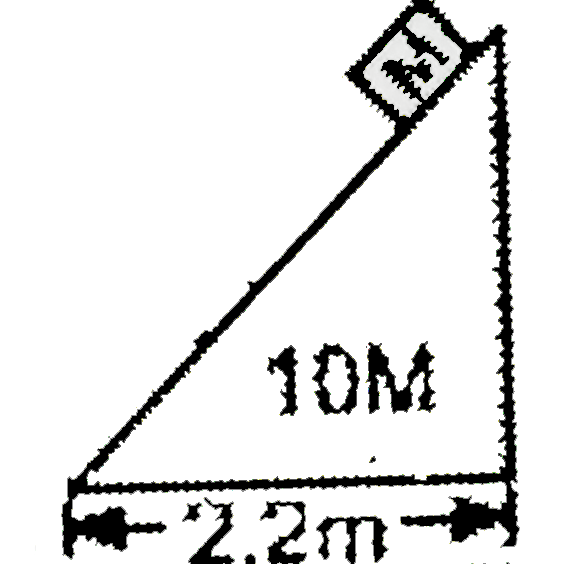 A0.22 mB0.20 mCzeroD0.24 m
A0.22 mB0.20 mCzeroD0.24 m
A block of mass M is placed on the top of a bigger block of mass 10 M as shown in figure. All the surfaces are frictionless. The system is released from rest, then the distance moved by the bigger block at the instant the smaller block reaches the ground :

View SolutionA block of mass m is placed at rest on a smooth wedge of mass M placed at rest on a smooth horizontal surface. As the system is released

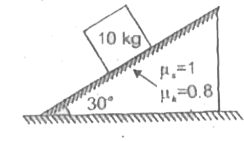
View SolutionA block of 10 kg mass is placed on a rough inclined surface as shown in figure. The acceleration of the block will be
View SolutionAssuming all the surfaces to be smooth, find the acceleration of the triangular block of mass M when the block of mass m slides on it.

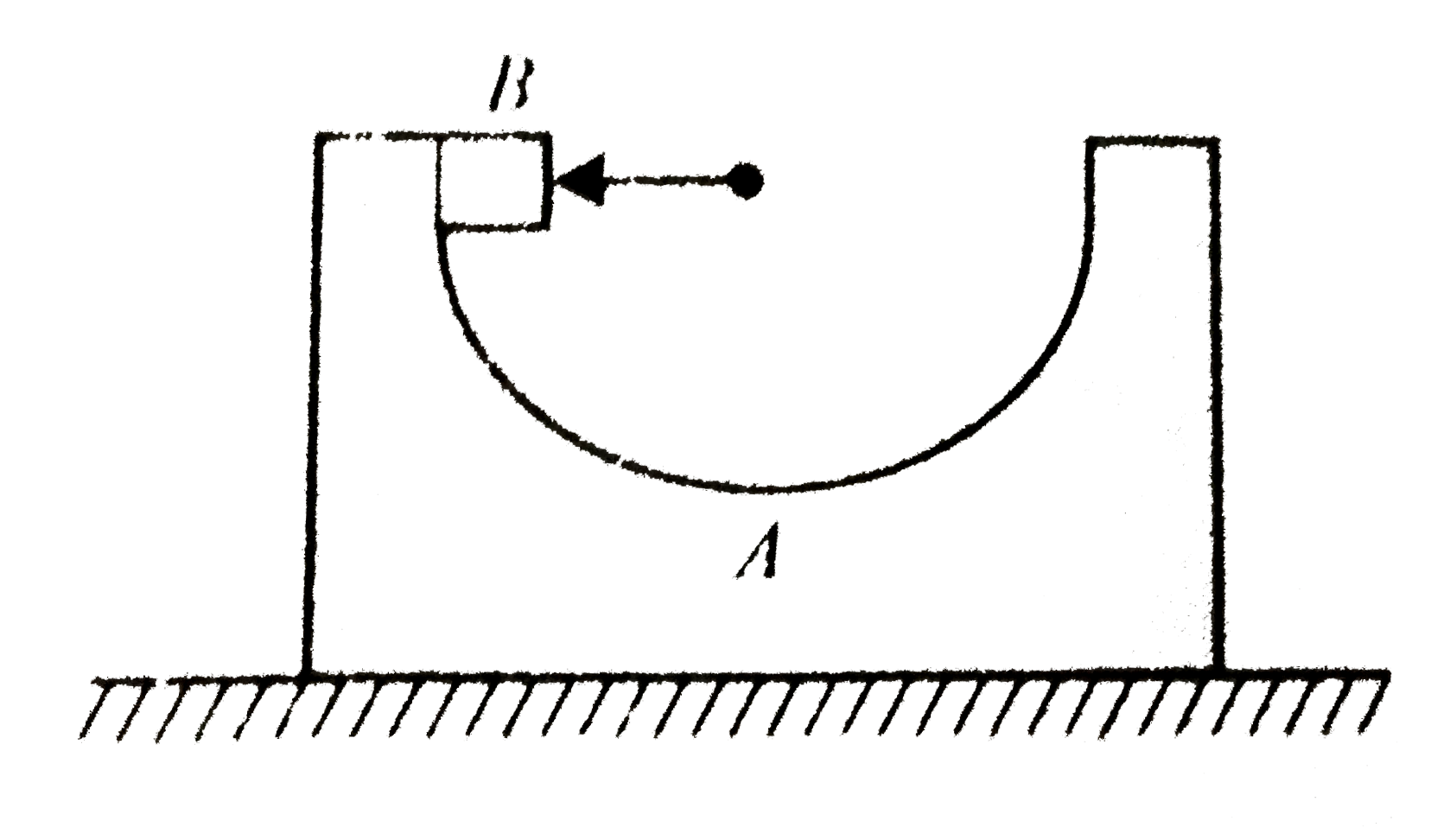
View SolutionFigure shows a block A of mass 6m having a smooth semicircular groove of radius a placed on a smooth horizontal surface. A block B of mass m is released from a position in groove where its radius is horizontal. Find the speed of the bigger block when the smaller block reaches its bottom most position.
View SolutionA block of mass m is pulled by a constant power P placed on a rough horizontal plane. The coeficient of friction between the block and surface is μ. Find the maximum velocity of the block.
View SolutionA block of mass 2 kg is pushed towards a very heavy object moving with 2 m/s closer to the block (as shown). Assuming elastic collision and frictionless surface, find the final velocities of the blocks.

View Solution
