A block of mass 5 kg is placed on a plank of mass 10 kg which is placed on the smooth horizontal surface as shown in figure. If a 100 N force is applied on the plank then the acceleration of the plank wrt ground is (Coefficient of friction between block and plank μs=μk=0.4 and g=10ms2)
8=ms2
2=ms2
6=ms2
Zero
The correct Answer is:A
To solve the problem, we need to determine the acceleration of the plank with respect to the ground when a force of 100 N is applied to it. We will consider the forces acting on both the block and the plank, as well as the friction between them.
1. Identify the Given Data:
- Mass of the block (m1) = 5 kg
- Mass of the plank (m2) = 10 kg
- Applied force (F) = 100 N
- Coefficient of friction (μ) = 0.4
- Acceleration due to gravity (g) = 10 m/s²
2. Calculate the Maximum Static Friction (F_max):
The maximum static friction that can act on the block is given by:
Fmax=μ⋅m1⋅g
Substituting the values:
Fmax=0.4⋅5kg⋅10m/s2=20N
3. Set Up the Equations of Motion:
- For the block (5 kg):
The friction force (F_f) is what causes the block to accelerate. Thus, we can write:
Ff=m1⋅a
where a is the acceleration of the block.
- For the plank (10 kg):
The net force acting on the plank is the applied force minus the friction force:
F−Ff=m2⋅a
Substituting Ff from the block's equation:
100−Ff=10⋅a
4. Combine the Equations:
From the block's equation, we have:
Ff=5⋅a
Substituting this into the plank's equation:
100−5a=10a
Rearranging gives:
100=15a
Therefore, solving for a:
a=10015=203≈6.67m/s2
5. Check if the Block Slips:
We need to check if the friction force required exceeds the maximum static friction:
Ff=5⋅a=5⋅203=1003≈33.33N
Since 33.33N>20N, the block will slip.
6. Calculate the Acceleration of the Plank:
When slipping occurs, we use kinetic friction:
Ffriction=μk⋅m1⋅g=20N
Now, the equation for the plank becomes:
100−20=10a
Simplifying gives:
80=10a⟹a=8m/s2
Final Answer:
The acceleration of the plank with respect to the ground is 8 m/s².
- Mass of the block (m1) = 5 kg
- Mass of the plank (m2) = 10 kg
- Applied force (F) = 100 N
- Coefficient of friction (μ) = 0.4
- Acceleration due to gravity (g) = 10 m/s²
The maximum static friction that can act on the block is given by:
Fmax=μ⋅m1⋅g
Substituting the values:
Fmax=0.4⋅5kg⋅10m/s2=20N
- For the block (5 kg):
The friction force (F_f) is what causes the block to accelerate. Thus, we can write:
Ff=m1⋅a
where a is the acceleration of the block.
The net force acting on the plank is the applied force minus the friction force:
F−Ff=m2⋅a
Substituting Ff from the block's equation:
100−Ff=10⋅a
From the block's equation, we have:
Ff=5⋅a
Substituting this into the plank's equation:
100−5a=10a
Rearranging gives:
100=15a
Therefore, solving for a:
a=10015=203≈6.67m/s2
We need to check if the friction force required exceeds the maximum static friction:
Ff=5⋅a=5⋅203=1003≈33.33N
Since 33.33N>20N, the block will slip.
When slipping occurs, we use kinetic friction:
Ffriction=μk⋅m1⋅g=20N
Now, the equation for the plank becomes:
100−20=10a
Simplifying gives:
80=10a⟹a=8m/s2
The acceleration of the plank with respect to the ground is 8 m/s².
Similar Questions
A block of mass 10kg is placed on a rough horizontal surface having coefficient of friction μ=0.5 . If a horizontal force of 100N is acting on it, then acceleration of the will be.
View SolutionA block of mass 10kg is placed on a rough horizontal surface having coefficient of friction μ=0.5 . If a horizontal force of 100N is acting on it, then acceleration of the will be.
View SolutionA sphere of mass m and radius r is placed on a rough plank of mass M. The system is placed on a smooth horizontal surface. A constant force F is applied on the plank such that the sphere rolls purely on the plank. Find the acceleration of the sphere.

View SolutionA block of mass 10kg is placed on a rough horizontal surface having coefficient of friction μ=0.5 . If a horizontal force of 100N is acting on it, then acceleration of the block will be.
View SolutionA block of mass 10kg is placed on a rough horizontal surface having coefficient of friction μ=0.5 . If a horizontal force of 100N is acting on it, then acceleration of the block will be.
View SolutionA man of mass 50 kg is pulling on a plank of mass 100 kg kept on a smooth floor as shown with force of 100 N. If both man & plank move together, find force of friction acting on man.

View SolutionA bolck of mass m =2 kg is placed on a plank of mass M = 10 kg, which is placed on a smooth horizontal plane as shown in the figure. The coefficient of friction between the block and the plank is μ=13. If a horizontal force F is applied on the plank, then the maximum value of F for which the block and the plank move together is (g=10m/s2)
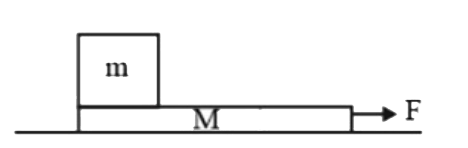
View SolutionA block A of mass 2kg is placed over smooth block B of mass 4kg which is placed over a smooth horizontal floor The coefficient of friction between A and B is 0.4 when a horizontal forces of magnitude 10N is applied on A the acceleration of block of A and B are

View SolutionA disc of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between disc and plank to prevent slipping. A force F is applied at the centre of the disc.

Acceleration of the plank is
View SolutionA block of negligible size and mass 2kg is placed above a plank of mass 4kg and length 16m as shown in figure. A force of 44N is applied on the lower block as shown in the figure. The ground is smooth, coefficient of friction between upper and lower block is 0.2. Find the time after which the upper block will fall over.
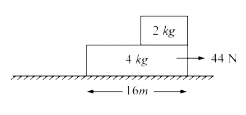
View Solution
