In given arrangement as shown in figure, the system is in equilibrium. Choose the correct option(g=10ms2)
T1=100√5N
θ=tan−1(2)
T1=100√3N
Both (1) and (2)
The correct Answer is:D
To solve the problem step by step, we will analyze the forces acting on the system and apply the conditions for equilibrium.
Step 1: Identify the Forces
In the given arrangement, we have two blocks with masses:
- Block 1: 20 grams (which is 0.02 kg)
- Block 2: 2 grams (which is 0.002 kg)
These blocks are connected by ropes and are in equilibrium. The forces acting on each block include the gravitational force and the tension in the ropes.
Step 2: Calculate the Gravitational Forces
Using the formula for weight (W = mg), we can calculate the gravitational forces acting on each block:
- For Block 1 (20 grams):
W1=m1⋅g=0.02kg⋅10m/s2=0.2N
- For Block 2 (2 grams):
W2=m2⋅g=0.002kg⋅10m/s2=0.02N
Step 3: Set Up the Equations for Tension
In equilibrium, the tension in the ropes must balance the weight of the blocks:
- Let T2 be the tension in the rope connected to Block 1 (20 grams).
- Let T3 be the tension in the rope connected to Block 2 (2 grams).
From the equilibrium conditions:
- For Block 1:
T2=W1=0.2N
- For Block 2:
T3=W2=0.02N
Step 4: Relate Tensions Using Angles
Assuming the ropes make an angle θ with the horizontal:
- The horizontal component of T1 (the tension in the rope connected to Block 1) is:
T1cosθ=T3
- The vertical component of T1 is:
T1sinθ=T2
Step 5: Substitute the Tension Values
Substituting the values of T2 and T3:
- From T1cosθ=0.02:
T1cosθ=0.02(1)
- From T1sinθ=0.2:
T1sinθ=0.2(2)
Step 6: Divide the Equations
Dividing equation (2) by equation (1):
T1sinθT1cosθ=0.20.02
This simplifies to:
tanθ=10
Step 7: Calculate θ
To find θ:
θ=tan−1(10)
Step 8: Calculate T1
Using either equation (1) or (2) to find T1:
From equation (1):
T1=0.02cosθ
Substituting θ:
T1=0.02cos(tan−1(10))
Using the identity cos(tan−1(x))=1√1+x2:
T1=0.021√1+102=0.02√101
Conclusion
Thus, the values for T1 and θ are:
- T1=0.02√101
- θ=tan−1(10)
In the given arrangement, we have two blocks with masses:
- Block 1: 20 grams (which is 0.02 kg)
- Block 2: 2 grams (which is 0.002 kg)
Using the formula for weight (W = mg), we can calculate the gravitational forces acting on each block:
- For Block 1 (20 grams):
W1=m1⋅g=0.02kg⋅10m/s2=0.2N
- For Block 2 (2 grams):
W2=m2⋅g=0.002kg⋅10m/s2=0.02N
In equilibrium, the tension in the ropes must balance the weight of the blocks:
- Let T2 be the tension in the rope connected to Block 1 (20 grams).
- Let T3 be the tension in the rope connected to Block 2 (2 grams).
- For Block 1:
T2=W1=0.2N
- For Block 2:
T3=W2=0.02N
Assuming the ropes make an angle θ with the horizontal:
- The horizontal component of T1 (the tension in the rope connected to Block 1) is:
T1cosθ=T3
- The vertical component of T1 is:
T1sinθ=T2
Substituting the values of T2 and T3:
- From T1cosθ=0.02:
T1cosθ=0.02(1)
- From T1sinθ=0.2:
T1sinθ=0.2(2)
Dividing equation (2) by equation (1):
T1sinθT1cosθ=0.20.02
This simplifies to:
tanθ=10
To find θ:
θ=tan−1(10)
Using either equation (1) or (2) to find T1:
From equation (1):
T1=0.02cosθ
Substituting θ:
T1=0.02cos(tan−1(10))
Using the identity cos(tan−1(x))=1√1+x2:
T1=0.021√1+102=0.02√101
Thus, the values for T1 and θ are:
- T1=0.02√101
- θ=tan−1(10)
Similar Questions
Choose the correct option(s)
View SolutionChoose the correct option (S)?
View SolutionChoose the correct option w.r.t given figure :
View SolutionFor the given situation shown in figure , choose the correct option (g=10m/s−2)

View SolutionObserve figures and choose the correct option.
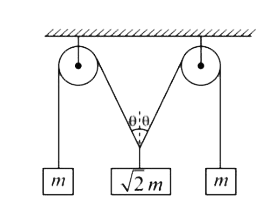
View SolutionThe pulley and strings shown in the figure are smooth and of negligible mass. For the system to remain in equilibrium, the angle θ should be:
View SolutionIn the circuit shown in figure it is given that Vb−Va=2 volt. Choose the correct options

View SolutionStudy the given figure and choose the correct option -

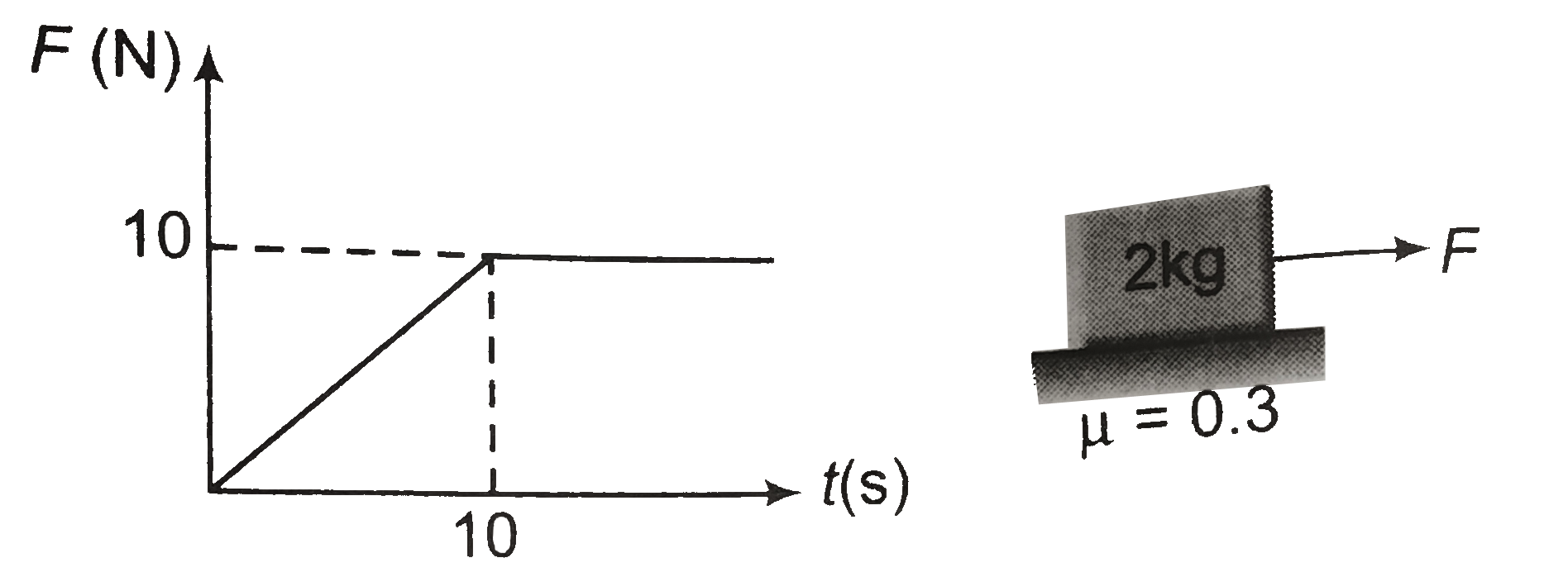
View SolutionForce acting on a block versus time graph is as shown in figure Choose the correct options.(g=10m/s−2)
View SolutionFor the system shown in figure , to be in equilibrium , determine mass m .

View Solution