A block of mass 10 kg is placed on the rough horizontal surface. A pulling force F is acting on the block which makes an angle θ above the horizontal. If coefficient of friction between block and surface is 43 then minimum value of force required to just move the block is (g=10ms2)
80 N
160 N
60 N
120 N
The correct Answer is:A
To solve the problem, we need to find the minimum pulling force F required to just move a block of mass 10kg on a rough horizontal surface, given that the coefficient of friction μ=43 and g=10m/s2.
1. Identify Given Values:
- Mass of the block, m=10kg
- Coefficient of friction, μ=43
- Acceleration due to gravity, g=10m/s2
2. Calculate the Weight of the Block:
W=mg=10kg×10m/s2=100N
3. Determine the Angle of Friction:
The angle of friction θ can be calculated using:
θ=tan−1(μ)=tan−1(43)
This angle corresponds to the condition when the block just begins to move.
4. Set Up the Force Equations:
- In the vertical direction:
N+Fsinθ=mg
Where N is the normal force.
- In the horizontal direction:
Fcosθ=f
Where f is the frictional force, given by:
f=μN
5. Express Normal Force N:
From the vertical force balance:
N=mg−Fsinθ
6. Substitute N into the Friction Equation:
The frictional force can be expressed as:
f=μ(mg−Fsinθ)
Substitute this into the horizontal force equation:
Fcosθ=μ(mg−Fsinθ)
7. Rearranging the Equation:
Fcosθ=43(100−Fsinθ)
Simplifying gives:
Fcosθ+43Fsinθ=4003
8. Factor out F:
F(cosθ+43sinθ)=4003
Thus,
F=4003(cosθ+43sinθ)
9. Substituting θ:
Using θ calculated from step 3, we can find cosθ and sinθ using trigonometric identities. For tanθ=43:
- sinθ=45
- cosθ=35
10. Final Calculation:
Substitute sinθ and cosθ into the equation:
F=4003(35+43⋅45)
Simplifying gives:
F=4003(35+1615)=4003(915+1615)=4003⋅2515=400⋅1575=80N
Conclusion:
The minimum value of the force required to just move the block is F=80N.
- Mass of the block, m=10kg
- Coefficient of friction, μ=43
- Acceleration due to gravity, g=10m/s2
W=mg=10kg×10m/s2=100N
The angle of friction θ can be calculated using:
θ=tan−1(μ)=tan−1(43)
This angle corresponds to the condition when the block just begins to move.
- In the vertical direction:
N+Fsinθ=mg
Where N is the normal force.
- In the horizontal direction:
Fcosθ=f
Where f is the frictional force, given by:
f=μN
From the vertical force balance:
N=mg−Fsinθ
The frictional force can be expressed as:
f=μ(mg−Fsinθ)
Substitute this into the horizontal force equation:
Fcosθ=μ(mg−Fsinθ)
Fcosθ=43(100−Fsinθ)
Simplifying gives:
Fcosθ+43Fsinθ=4003
F(cosθ+43sinθ)=4003
Thus,
F=4003(cosθ+43sinθ)
Using θ calculated from step 3, we can find cosθ and sinθ using trigonometric identities. For tanθ=43:
- sinθ=45
- cosθ=35
Substitute sinθ and cosθ into the equation:
F=4003(35+43⋅45)
Simplifying gives:
F=4003(35+1615)=4003(915+1615)=4003⋅2515=400⋅1575=80N
The minimum value of the force required to just move the block is F=80N.
Similar Questions
A block of weight 200N is pulled along a rough horizontal surface at constant speed by a force 100N acting at an angle 30∘ above the horizontal. The coefficient of friction between the block and the surface is
View SolutionA wooden block of mass M resting on a rough horizontal surface is pulled with a force T at an angle q to the horizontal. If m is coefficient of kinetic friction between the block and the surface, the acceleration of the block is
View SolutionA block of mass 10 kg is moving on a rough surface as shown in figure. The frictional force acting on block is :-
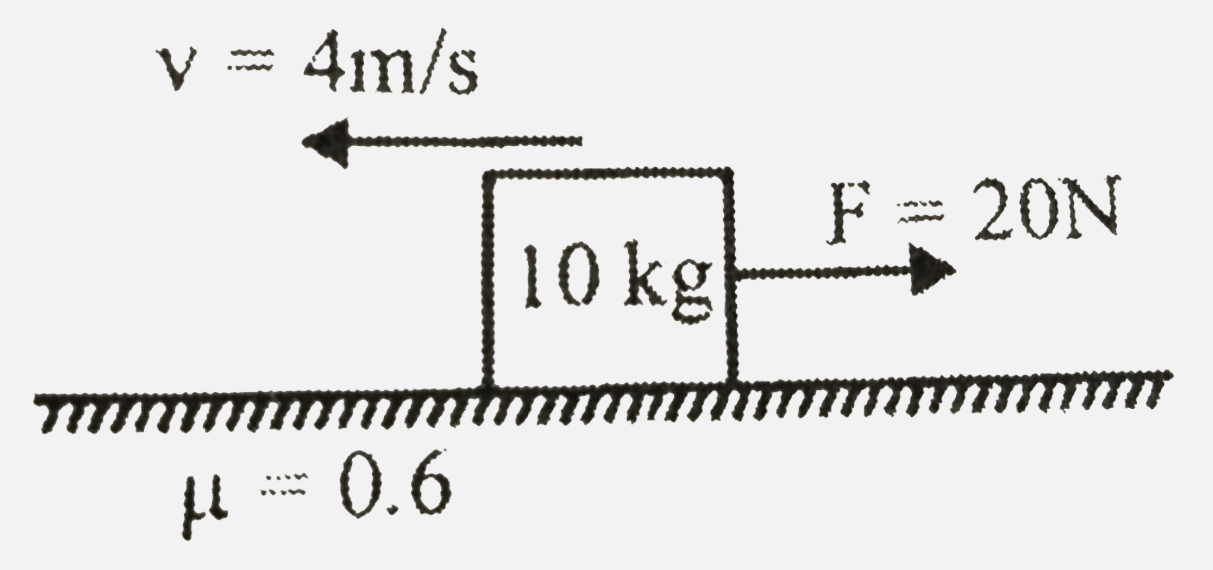 View Solution
View SolutionA block of mass 10 kg is placed on a rough horizontal surface of coefficient of friction 0.1. A pulling force of 100 N acts on it at 37∘ with the horizontal. The frictional force acting on the body is ..... N.
View SolutionA block of mass 4kg is placed on a rough horizontal plane A time dependent force F=kt2 acts on the block where k=2N/s2 Coefficient of friction μ=0.8 force of friction between the block and the plane at t=2s is
View SolutionA block is sliding on a rough horizontal surface. If the contact force on the block is √2 times the frictional force, the coefficient of friction is
View SolutionA block of mass m is at rest on a rough inclined plane of angle of inclination θ. If coefficient of friction between the block and the inclined plane is μ, then the minimum value of force along the plane required to move the block on the plane is
View SolutionA block of mass m is placed at rest on a horizontal rough surface with angle of friction ϕ. The block is pulled with a force F at an angle θ with the horizontal. The minimum value of F required to move the block is
View SolutionA block of mass m is placed at rest on a horizontal rough surface with angle of friction ϕ. The block is pulled with a force F at an angle θ with the horizontal. The minimum value of F required to move the block is
View SolutionA force F is acting at an angle θ with horizontal on a block of mass 12 kg placed on a rough 3 horizontal surface having coefficient of friction μ=34 as shown in the figure. The minimum value of force F to just move the block will be (g=10ms−2)
View Solution

