Two blocks of masses 10 kg and 9 kg are connected with light string which is passing over an ideal pulley as shown in figure. If system is released from rest then the acceleration of 9 kg block at the given instant is about (Assume all the surfaces are smooth and g=10ms2)
1.8ms2
4.73ms2
3.5ms2
3ms2
The correct Answer is:B
To find the acceleration of the 9 kg block in the given system, we can follow these steps:
Step 1: Identify the forces acting on the blocks
- For the 10 kg block (Block A), the forces acting on it are:
- Weight (downward) = WA=mA⋅g=10kg⋅10m/s2=100N
- Tension (upward) = T
- For the 9 kg block (Block B), the forces acting on it are:
- Weight (downward) = WB=mB⋅g=9kg⋅10m/s2=90N
- Tension (upward) = T
Step 2: Write the equations of motion for both blocks
- For Block A (10 kg):
WA−T=mA⋅aA(1)
Substituting the values:
100−T=10⋅aA(1)
- For Block B (9 kg):
WB−T=mB⋅aB(2)
Substituting the values:
90−T=9⋅aB(2)
Step 3: Relate the accelerations of the blocks
Since the blocks are connected by a string over a pulley, the acceleration of the two blocks will be related. If we assume the downward acceleration of the 9 kg block is a, then the upward acceleration of the 10 kg block will be aA=a.
Step 4: Solve the equations
From equation (1):
100−T=10a⇒T=100−10a(3)
From equation (2):
90−T=9a⇒T=90−9a(4)
Step 5: Set equations (3) and (4) equal to each other
100−10a=90−9a
Step 6: Solve for a
Rearranging gives:
100−90=10a−9a
10=a
a=10m/s2
Step 7: Find the acceleration of the 9 kg block
Since the 9 kg block is accelerating downward, its acceleration is:
aB=a=10m/s2
Final Result
The acceleration of the 9 kg block is 10m/s2.
---
- For the 10 kg block (Block A), the forces acting on it are:
- Weight (downward) = WA=mA⋅g=10kg⋅10m/s2=100N
- Tension (upward) = T
- Weight (downward) = WB=mB⋅g=9kg⋅10m/s2=90N
- Tension (upward) = T
- For Block A (10 kg):
WA−T=mA⋅aA(1)
Substituting the values:
100−T=10⋅aA(1)
WB−T=mB⋅aB(2)
Substituting the values:
90−T=9⋅aB(2)
Since the blocks are connected by a string over a pulley, the acceleration of the two blocks will be related. If we assume the downward acceleration of the 9 kg block is a, then the upward acceleration of the 10 kg block will be aA=a.
From equation (1):
100−T=10a⇒T=100−10a(3)
90−T=9a⇒T=90−9a(4)
100−10a=90−9a
Rearranging gives:
100−90=10a−9a
10=a
a=10m/s2
Since the 9 kg block is accelerating downward, its acceleration is:
aB=a=10m/s2
The acceleration of the 9 kg block is 10m/s2.
Similar Questions
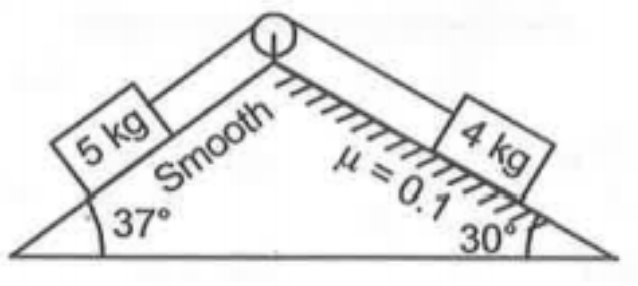
Two blocks of masses 5 kg and 4 kg are connected with ideal string which is passing over an ideal pulley as shown in figure. If the system is released from rest then the magnitude of acceleration of the blocks will be (Take g=10ms−2and√3=1.7)
View SolutionTwo blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.

View SolutionTwo blocks each of mass 4 kg connected by a light string which is passing over an ideal pulley is as shown in figure. If the system is released from rest then the acceleration (in m/s2) of centre of mass is (g = 10 m/s2)
View SolutionTwo blocks are connected by a long inextensible string passing over an ideal pulley as shown in the figure. If the system is released from rest then the common speed of blocks when block m2 moves a distance I will be
View SolutionTwo bodies of masses 1 kg and 2 kg are connected by a very light string passed over a clamped light smooth pulley. If the system is released from rest, find the acceleration of the two masses and the tension in the string
View SolutionA block of mass 5kg is hung with the help of light string which is passing over an ideal pulley as shown as in figure.The force is exerted by the clamp on the pulley will be (g= 10 m/s^2)
_PHY_E05_165_Q01.png)
View SolutionTwo masses of 10 kg and 20 kg are connected with an inextensible string passing over two smooth pulleys as shown in the figure. The acceleration of 20 kg mass will be :
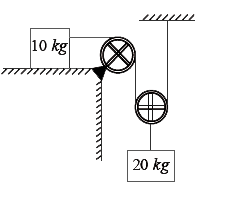
View SolutionTwo blocks of masses 6kg and 4kg are attached to the two ends of a massless string passing over a smooth fixed pulley. if the system is released, the acceleration of the centre of mass of the system will be
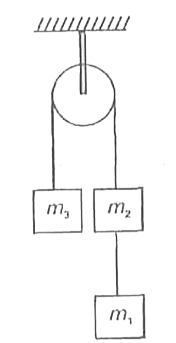
View SolutionThree blocks of masses m1=4kg,m2=2kg,m3=4kg are connected with ideal strings passing over a smooth, massless pulley as shown in figure. The acceleration of blocks will be (g=10m/s2)
View SolutionTwo unequal masses of 1kg and 2kg are connected by an inextensible light string passing over a smooth pulley as shown in figure. A force F=20N is applied on 1kg block find the acceleration of either block (g=10m/s2).

View Solution
