Two blocks are connected by a long inextensible string passing over an ideal pulley as shown in the figure. If the system is released from rest then the common speed of blocks when block m2 moves a distance I will be
√(μm1−m2)gLm1+m2
√(m1−m2)gLμ(m1+m2)
√2(m2−μm1)gLm1+m2
Zero
To solve the problem of finding the common speed of two blocks connected by a long inextensible string passing over an ideal pulley, we can follow these steps:
Step 1: Understand the System
We have two blocks, m1 and m2, connected by a string over a pulley. When released from rest, block m2 moves downward, causing block m1 to move upward.
Step 2: Apply Newton's Second Law
For block m1 (moving upward):
T−μm1g=m1a(1)
where T is the tension in the string, μ is the coefficient of friction, g is the acceleration due to gravity, and a is the acceleration of the blocks.
For block m2 (moving downward):
m2g−T=m2a(2)
Step 3: Solve for Tension and Acceleration
From equation (1):
T=μm1g+m1a
Substituting T into equation (2):
m2g−(μm1g+m1a)=m2a
Rearranging gives:
m2g−μm1g−m1a=m2a
Combining terms:
m2g−μm1g=m1a+m2a
Factoring out a:
m2g−μm1g=(m1+m2)a
Thus, we can solve for a:
a=m2g−μm1gm1+m2(3)
Step 4: Use Kinematics to Find Speed
Since the system starts from rest, the initial speed u=0. The distance moved by block m2 is L. Using the kinematic equation:
v2−u2=2as
Substituting u=0 and s=L:
v2=2aL
Substituting a from equation (3):
v2=2L(m2g−μm1gm1+m2)
Thus, we can express v:
v=√2L(m2g−μm1gm1+m2)
Step 5: Final Expression for Speed
The common speed of the blocks when block m2 moves a distance L is:
v=√2L(m2−μm1)gm1+m2
We have two blocks, m1 and m2, connected by a string over a pulley. When released from rest, block m2 moves downward, causing block m1 to move upward.
For block m1 (moving upward):
T−μm1g=m1a(1)
where T is the tension in the string, μ is the coefficient of friction, g is the acceleration due to gravity, and a is the acceleration of the blocks.
m2g−T=m2a(2)
From equation (1):
T=μm1g+m1a
m2g−(μm1g+m1a)=m2a
Rearranging gives:
m2g−μm1g−m1a=m2a
Combining terms:
m2g−μm1g=m1a+m2a
Factoring out a:
m2g−μm1g=(m1+m2)a
Thus, we can solve for a:
a=m2g−μm1gm1+m2(3)
Since the system starts from rest, the initial speed u=0. The distance moved by block m2 is L. Using the kinematic equation:
v2−u2=2as
Substituting u=0 and s=L:
v2=2aL
Substituting a from equation (3):
v2=2L(m2g−μm1gm1+m2)
Thus, we can express v:
v=√2L(m2g−μm1gm1+m2)
The common speed of the blocks when block m2 moves a distance L is:
v=√2L(m2−μm1)gm1+m2
Topper's Solved these Questions
Similar Questions
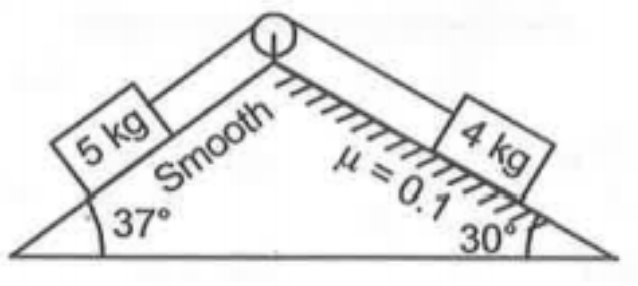
Two blocks of masses 5 kg and 4 kg are connected with ideal string which is passing over an ideal pulley as shown in figure. If the system is released from rest then the magnitude of acceleration of the blocks will be (Take g=10ms−2and√3=1.7)
View SolutionTwo blocks each of mass 4 kg connected by a light string which is passing over an ideal pulley is as shown in figure. If the system is released from rest then the acceleration (in m/s2) of centre of mass is (g = 10 m/s2)
View Solution
Knowledge Check
Two blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.
 A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2

An ideal string pulley system is shown in the figure and system is released from rest choose correct option
View SolutionTwo blocks of masses 10 kg and 9 kg are connected with light string which is passing over an ideal pulley as shown in figure. If system is released from rest then the acceleration of 9 kg block at the given instant is about (Assume all the surfaces are smooth and g=10ms2)
View SolutionTwo unequal masses of 1 kg and 2 kg are attached at the two ends of a light inextensible string passing over a smooth pulley as shown in figure. If the system is released from rest, find the work done by string on both the blocks in 1 s. (Take g = 10 ms−2)

View SolutionTwo blocks A and B are joined by means of a slacked string passing over a massless pulley as shown in Figure. The system is released from rest and it becomes taut when B falls a distance 0.5m.
a. Find the common velocity of the two blocks just after the string becomes taut.
b. Find the magnitude of impulse on the pulley by the clamp during the small interval while string becomes taut.

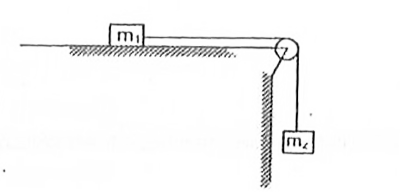
View SolutionA block of mass m1=2 kg is kept on a smooth horizontal table. Another block of mass m2=1 kg is connected to m1 by a light inextensible string passing over a smooth pulley as shown in the figure. If the blocks are released, what will be the (a) acceleration of each block (b) tension in the string?
View SolutionTwo unequal masses of 1 kg and 2 kg are attached at the two ends of a light inextensible string passing over a smooth pulley as shown . If the system is released from rest, find the work done by string on both the blocks in 1 s.
(Take g=10m/s2).
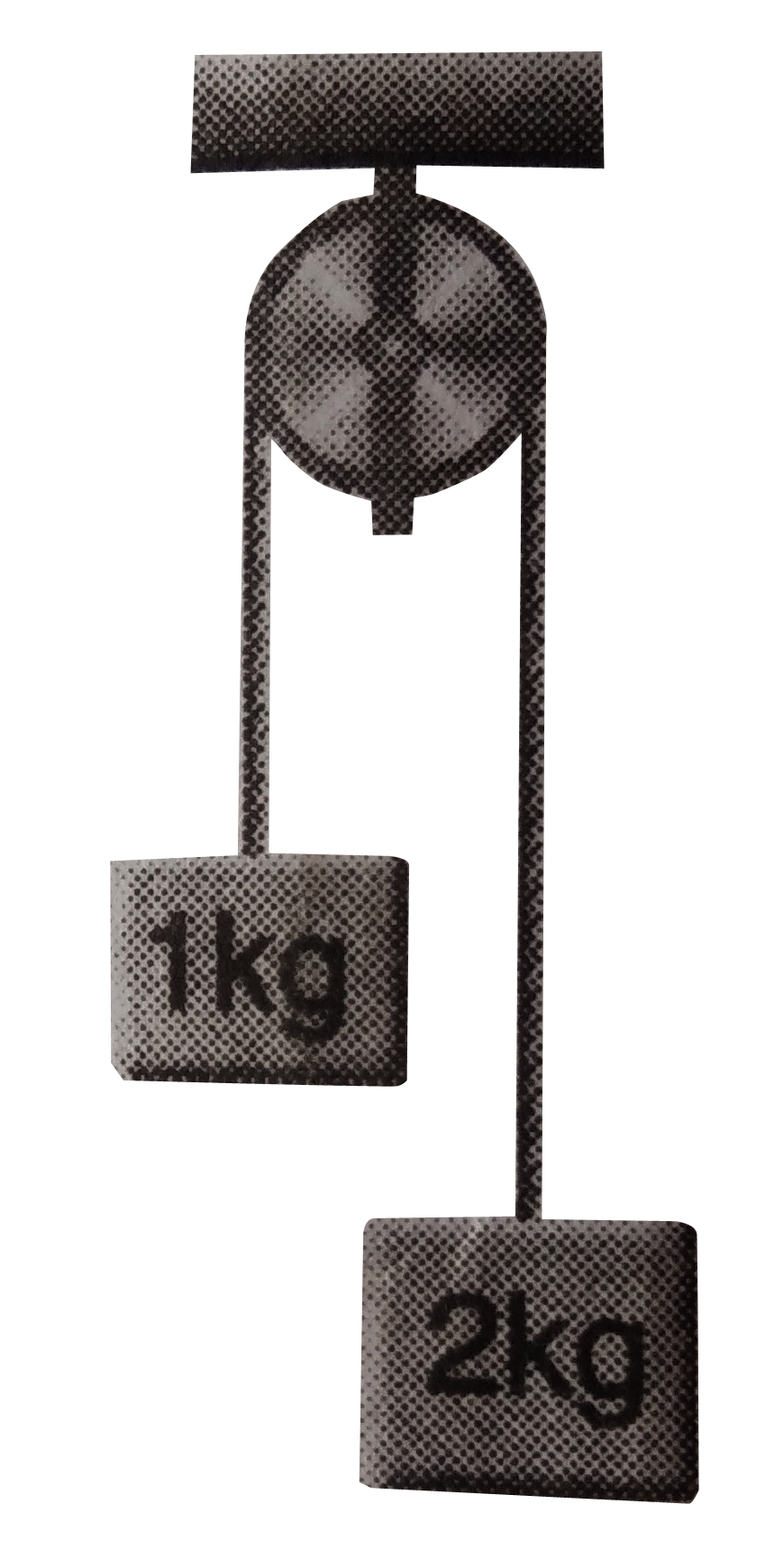
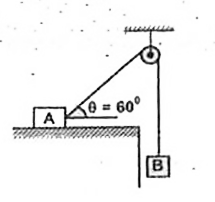
View SolutionTwo blocks A & B are connected by a light inextensible string passing over a fixed smooth pulley as shown in the figure. The coefficient of friction between the block A and the horizontal table is μ=0.2. If the block A is just to slip, find the ratio of the masses of the blocks.
View Solution
