The height of mercury in the barometer tube is 70cm due to entrapped air in it as shown in figure. Now from this position tube is pulled up slightly, then length of the mercury column in the tube will
Remain 70cm
Slightly more than 70cm
Slightly less than 70cm
Can't say
To solve the problem, we need to analyze the situation of a barometer tube containing mercury and entrapped air. The initial height of the mercury column is given as 70 cm. When the tube is pulled up slightly, we need to determine the new height of the mercury column.
1. Understanding the Initial Condition:
The barometer tube initially has mercury at a height of 70 cm due to atmospheric pressure acting on the mercury in the reservoir. The air trapped in the tube creates a pressure that balances the weight of the mercury column.
2. Effect of Pulling the Tube Up:
When the tube is pulled up slightly, the volume of the air above the mercury column increases. According to Boyle's Law, the pressure of a gas is inversely proportional to its volume when temperature is constant.
3. Applying Boyle's Law:
Let the initial volume of the air be V1 and the initial pressure be P1. When the tube is pulled up, the new volume becomes V2 and the new pressure becomes P2. According to Boyle's Law:
P1V1=P2V2
4. Pressure Considerations:
The pressure at the top of the mercury column (where the air is trapped) is equal to the atmospheric pressure minus the pressure due to the mercury column:
Pair=Patm−ρgh
where ρ is the density of mercury, g is the acceleration due to gravity, and h is the height of the mercury column.
5. New Height of Mercury Column:
As the tube is pulled up, the height of the mercury column will decrease because the pressure of the air trapped above the mercury will decrease as its volume increases. The mercury will rise in the tube until a new equilibrium is reached.
6. Conclusion:
Since the air pressure decreases when the tube is pulled up, the mercury column will not remain at 70 cm. Instead, it will fall to a new height. The exact new height can be determined by considering the new volume of air and applying Boyle's Law, but qualitatively we can say that the height of the mercury column will be less than 70 cm.
Final Answer:
The length of the mercury column in the tube will be less than 70 cm.
---
The barometer tube initially has mercury at a height of 70 cm due to atmospheric pressure acting on the mercury in the reservoir. The air trapped in the tube creates a pressure that balances the weight of the mercury column.
When the tube is pulled up slightly, the volume of the air above the mercury column increases. According to Boyle's Law, the pressure of a gas is inversely proportional to its volume when temperature is constant.
Let the initial volume of the air be V1 and the initial pressure be P1. When the tube is pulled up, the new volume becomes V2 and the new pressure becomes P2. According to Boyle's Law:
P1V1=P2V2
The pressure at the top of the mercury column (where the air is trapped) is equal to the atmospheric pressure minus the pressure due to the mercury column:
Pair=Patm−ρgh
where ρ is the density of mercury, g is the acceleration due to gravity, and h is the height of the mercury column.
As the tube is pulled up, the height of the mercury column will decrease because the pressure of the air trapped above the mercury will decrease as its volume increases. The mercury will rise in the tube until a new equilibrium is reached.
Since the air pressure decreases when the tube is pulled up, the mercury column will not remain at 70 cm. Instead, it will fall to a new height. The exact new height can be determined by considering the new volume of air and applying Boyle's Law, but qualitatively we can say that the height of the mercury column will be less than 70 cm.
The length of the mercury column in the tube will be less than 70 cm.
Similar Questions
The vertical height of mercury in a simple barometer is dependant on the area of cross-section of barometer tube.
View Solution
If the above tube is kept in vertical position by how much length the mercury column descends ?
View SolutionA barometer tube reads 76 cm of mercury. If the tube is gradually inclined at an angle of 60 with vertical, keeping the open end immersed in the mercury reservoir, the length of the mercury column will be
View SolutionIn given figure, an ideal gas is trapped between a mercury column and the closed end of a uniform vertical tube. The upper end of the tube is open to the atmosphere. Initially the lengths of the mercury column and the trapped air colume are 12cm and 50cm respectively. when the tube is titted solwly in a vertical plane through an angle of 30∘ with horizontal then the new length of air colume is x41m. Find x. Assuming the temperature to remains constant. (Patm=76cmofHg)
View SolutionA barometer tube reads 76 cm of Hg. If tube is : gradually inclined at an angle of 60∘ with vertical, keeping the open end in the mercury reservoir, the length of mercury column will be
View SolutionThe mercury manometer consists if two unequal arms of equal cross section 1 cm^(2) and lenghths 100cm and 50cm. The two open ends are sealed with air in the tube at a pressure of 80cm of mercurey. Some amount of mercury is now introduced in the manometer through the stopcock connected to it. If mercury rises in the shorter tube to a lenght 10cm in steady state, find the length of the mercury column risen in the longer tube.
View SolutionWater rises in a vertical capillary tube up to a length of 10 cm. If the tube is inclined at 45∘, the length of water risen in the tube will be
View SolutionWater rises to a height h in a capillary tube lowered vertically into water to a depth l as shown in the figure. The lower end of the tube is now closed, the tube is the taken out of the water and opened again. The length of the water column remaining in the tube will be
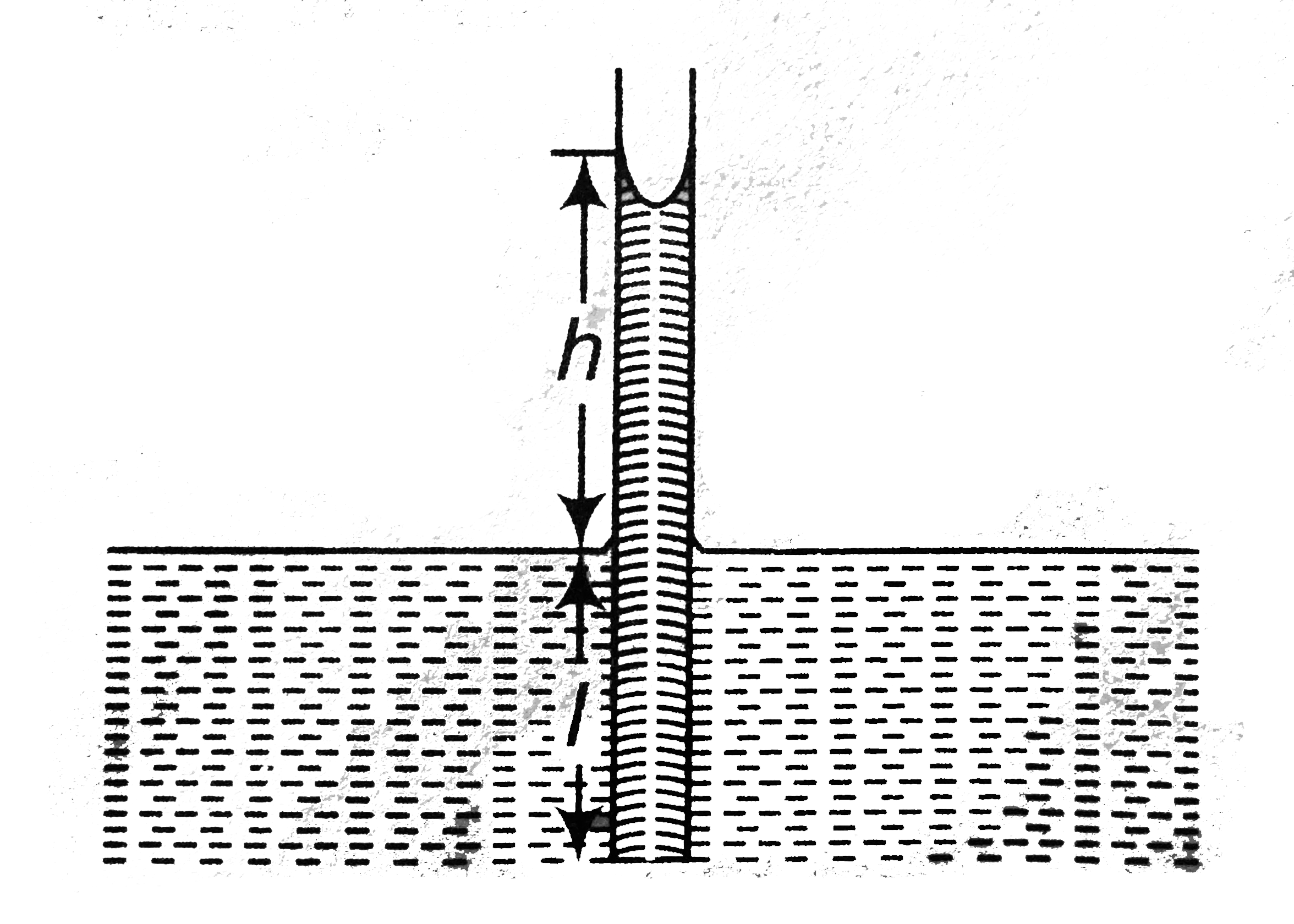 .
.
View SolutionA capillary tube is dipped in water to a depth and the water rises to a height h(<l) in the capillary tube. The lower end of the tube is closed in water by putting a lower over it. The tube is now taken out and the thumb is removed from the lower end and it kept open. The length of liquid column in the tube will be

View SolutionA uniform tube closed at aone end, contains a pellet of mercury 10cm long. When the tube is lept vertically with the closed-end upward, the length of the air column trapped is 20cm. Find the length of the air column trapped when the tube is inverted so that the closed-end goes down. Atmospheric pressure=75cm of mercury.
View Solution
