A barometer tube reads 76 cm of Hg. If tube is : gradually inclined at an angle of 60∘ with vertical, keeping the open end in the mercury reservoir, the length of mercury column will be
152cm
76cm
38cm
38√3 cm
To solve the problem of finding the length of the mercury column in an inclined barometer tube, we can follow these steps:
1. Understand the Initial Conditions:
- The barometer tube reads 76 cm of mercury when it is vertical. This means that the height of the mercury column (H) in the vertical position is 76 cm.
2. Identify the Angle of Inclination:
- The tube is inclined at an angle of 60∘ with the vertical.
3. Establish the Relationship Between Vertical and Inclined Heights:
- When the tube is inclined, the height of the mercury column (H) can be related to the length of the mercury column in the inclined tube (SI) using trigonometric relationships.
- The vertical height (H) can be expressed in terms of the inclined length (SI) using the cosine of the angle:
H=SI⋅cos(60∘)
4. Calculate the Cosine of the Angle:
- We know that cos(60∘)=12.
5. Substitute the Values:
- Rearranging the equation gives:
SI=Hcos(60∘)=H12=2H
- Since H=76cm, we substitute this value:
SI=2×76cm=152cm
6. Conclusion:
- The length of the mercury column in the inclined tube is 152cm.
Final Answer:
The length of the mercury column when the tube is inclined at 60∘ is 152 cm.
- The barometer tube reads 76 cm of mercury when it is vertical. This means that the height of the mercury column (H) in the vertical position is 76 cm.
- The tube is inclined at an angle of 60∘ with the vertical.
- When the tube is inclined, the height of the mercury column (H) can be related to the length of the mercury column in the inclined tube (SI) using trigonometric relationships.
- The vertical height (H) can be expressed in terms of the inclined length (SI) using the cosine of the angle:
H=SI⋅cos(60∘)
- We know that cos(60∘)=12.
- Rearranging the equation gives:
SI=Hcos(60∘)=H12=2H
- Since H=76cm, we substitute this value:
SI=2×76cm=152cm
- The length of the mercury column in the inclined tube is 152cm.
The length of the mercury column when the tube is inclined at 60∘ is 152 cm.
Similar Questions
A barometer tube reads 76 cm of mercury. If the tube is gradually inclined at an angle of 60 with vertical, keeping the open end immersed in the mercury reservoir, the length of the mercury column will be
View SolutionA barometer tube reads 76 cm of mercury. If the tube is gradually inclined keeping the open end immersed in the mercury reservoir, will the length of mercury column be 76 cm, more than 76 cm or less than 76 cm?
View Solution
Knowledge Check
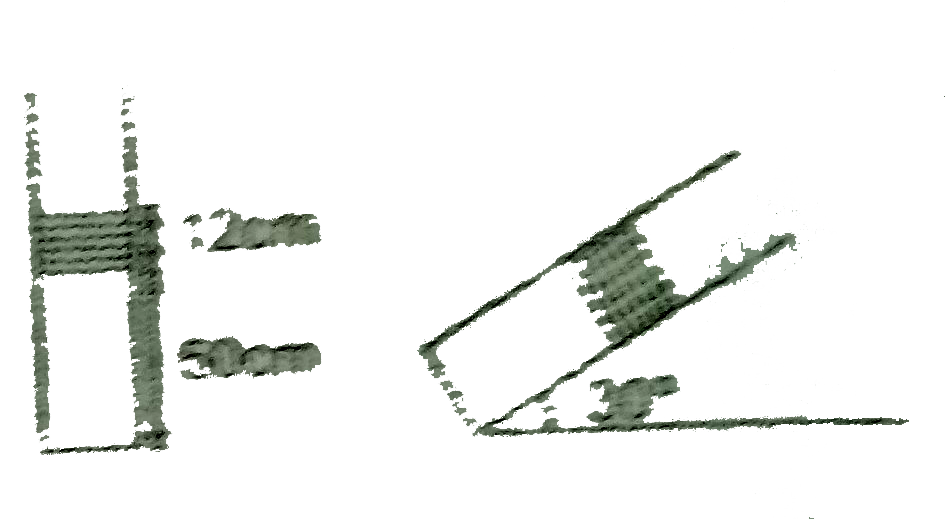
A thin tube of uniform cross-section is sealed at both ends. It lies horizontally, the middle 5 cm containing mercury and the two equal end containing air at the same pressure P. When the tube is held at an angle of 60∘ with the vetical direction, the length of the air column above and below the mercury column are 46 cm and 44.5 cm respectively. Calculate the pressure P in centimeters of mercury. (The temperature of the system is kept at 30∘C).
A75.4B45.8C67.5D89.3
Water rises in a capillary tube to a height 4 cm. If the tube is inclined at an angle of 45∘ with the vertical , find the position of the water in the tube.
View Solution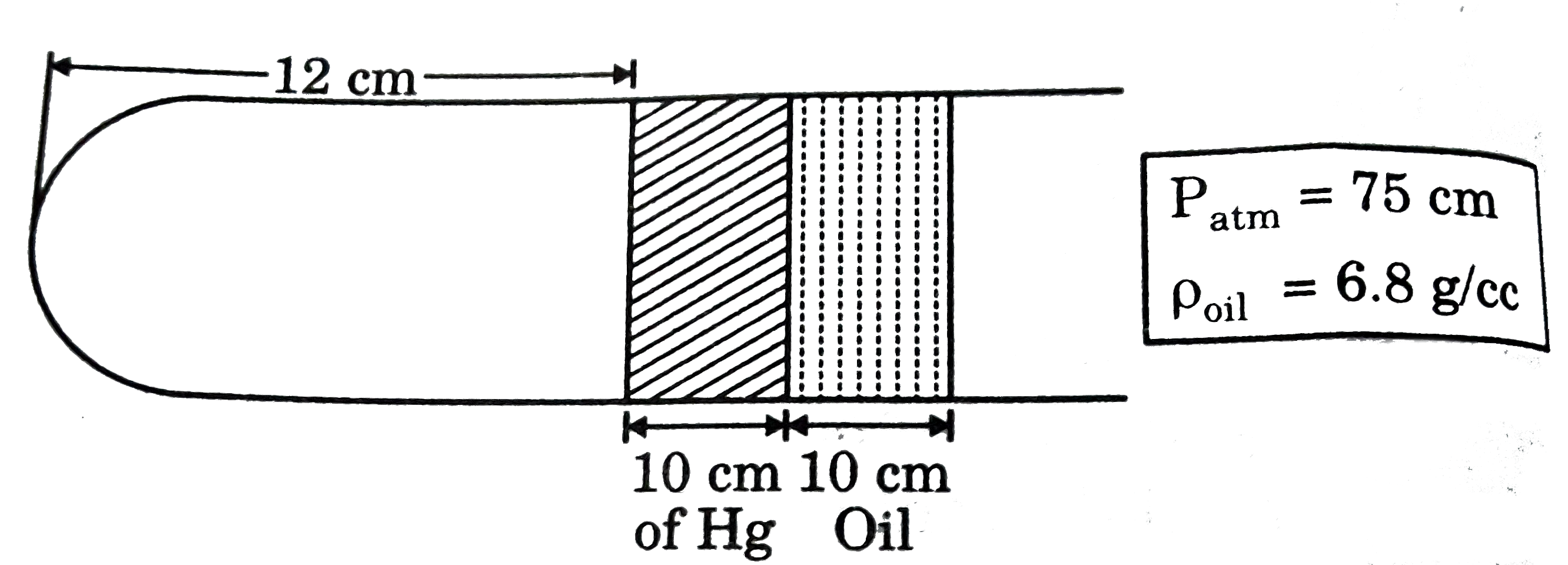
If above tube is placed vertically with the open and upward then find the length of the air column.
View SolutionA thin tube of uniform cross-section is sealed at both ends. It lies horizontally, the middle 5 cm containing mercury and the two equal end containing air at the same pressure P. When the tube is held at an angle of 60∘ with the vetical direction, the length of the air column above and below the mercury column are 46 cm and 44.5 cm respectively. Calculate the pressure P in centimeters of mercury. (The temperature of the system is kept at 30∘C).
View SolutionWater rises in a vertical capillary tube up to a height of 2.0 cm. If the tube is inclined at an angle of 60∘ with the vertical, then up to what length the water will rise in the tube ?
View SolutionThe height of mercury in the barometer tube is 70cm due to entrapped air in it as shown in figure. Now from this position tube is pulled up slightly, then length of the mercury column in the tube will
View SolutionIn given figure, an ideal gas is trapped between a mercury column and the closed end of a uniform vertical tube. The upper end of the tube is open to the atmosphere. Initially the lengths of the mercury column and the trapped air colume are 12cm and 50cm respectively. when the tube is titted solwly in a vertical plane through an angle of 30∘ with horizontal then the new length of air colume is x41m. Find x. Assuming the temperature to remains constant. (Patm=76cmofHg)
View SolutionAir is trapped in a horizontal glass tube by 36 cm mercury column as shown below :
 If the tube is held vertical keeping the open end up, lengh of air column shrink to 19 cm. What is the lengh (in cm) by which the mercury column shifts down?
If the tube is held vertical keeping the open end up, lengh of air column shrink to 19 cm. What is the lengh (in cm) by which the mercury column shifts down?
View Solution
