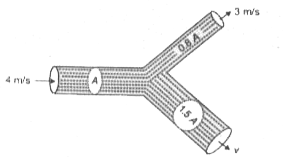
An incompressible liquid is flowing through Aa horizontal pipe as shown in figure. The magnitude of velocity v is
1 m/s
23 m/s
32 m/s
2 m/s
To solve the problem of an incompressible liquid flowing through a horizontal pipe, we can apply the principle of continuity and Bernoulli's equation. Here’s a step-by-step solution:
Step 1: Understand the Principle of Continuity
The principle of continuity states that for an incompressible fluid flowing through a pipe, the product of the cross-sectional area (A) and the velocity (v) at any two points along the pipe is constant. This can be expressed as:
A1v1=A2v2
where:
- A1 and A2 are the cross-sectional areas at points 1 and 2,
- v1 and v2 are the velocities at points 1 and 2.
Step 2: Apply Bernoulli's Equation
Bernoulli's equation relates the pressure, velocity, and height at two points in a flowing fluid. For a horizontal pipe, it can be simplified to:
P1+12ρv21=P2+12ρv22
where:
- P1 and P2 are the pressures at points 1 and 2,
- ρ is the density of the fluid,
- v1 and v2 are the velocities at points 1 and 2.
Step 3: Identify Given Values
From the problem, identify the values of the cross-sectional areas and the velocities at the two points. If the areas are given as A1 and A2, and if one of the velocities is known, we can find the other using the continuity equation.
Step 4: Solve for Unknowns
Using the continuity equation, if A1 and A2 are known, we can express one velocity in terms of the other:
v2=A1A2v1
Then, substitute v2 into Bernoulli's equation to solve for the unknown pressures or velocities.
Step 5: Final Calculation
After substituting the known values into the equations, perform the calculations to find the unknown velocity or pressure.
Example Calculation
Assuming A1=2m2, A2=1m2, and v1=3m/s:
1. From continuity:
v2=A1A2v1=21×3=6m/s
2. If pressures P1 and P2 are given, apply Bernoulli's equation to find the relationship between them.
The principle of continuity states that for an incompressible fluid flowing through a pipe, the product of the cross-sectional area (A) and the velocity (v) at any two points along the pipe is constant. This can be expressed as:
A1v1=A2v2
where:
- A1 and A2 are the cross-sectional areas at points 1 and 2,
- v1 and v2 are the velocities at points 1 and 2.
Bernoulli's equation relates the pressure, velocity, and height at two points in a flowing fluid. For a horizontal pipe, it can be simplified to:
P1+12ρv21=P2+12ρv22
where:
- P1 and P2 are the pressures at points 1 and 2,
- ρ is the density of the fluid,
- v1 and v2 are the velocities at points 1 and 2.
From the problem, identify the values of the cross-sectional areas and the velocities at the two points. If the areas are given as A1 and A2, and if one of the velocities is known, we can find the other using the continuity equation.
Using the continuity equation, if A1 and A2 are known, we can express one velocity in terms of the other:
v2=A1A2v1
After substituting the known values into the equations, perform the calculations to find the unknown velocity or pressure.
Assuming A1=2m2, A2=1m2, and v1=3m/s:
1. From continuity:
v2=A1A2v1=21×3=6m/s
Similar Questions
Knowledge Check
A liquid flows through a horizontal tube as shown in figure. The velocities of the liquid in the two sections, which have areas of cross-section A1 and A2 and v1 and v2 respectively. The differnece in the levels of the liquid in the two vertical tubes is h. then
 Av22−v21=2ghBv22+v21=2ghCv22−v21=ghDv22+v21=gh
Av22−v21=2ghBv22+v21=2ghCv22−v21=ghDv22+v21=gh
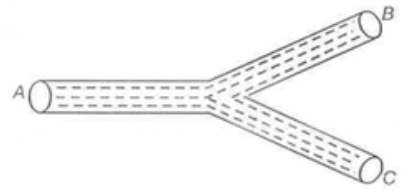
An incompressible liquid is flowing through a horizontal pipe as shown in figure. If V1,V2 and v3 be the velocity and a,a2 and a3 be the area of orifice A, B and C respectively, then
View SolutionAn incompressible liquid flows through a horizontal tube as shown in the figure. Then the velocity 'v' of the fluid is:

View SolutionA liquid is flowing through horizonatal pipes as shown in figure. The value of speed v is
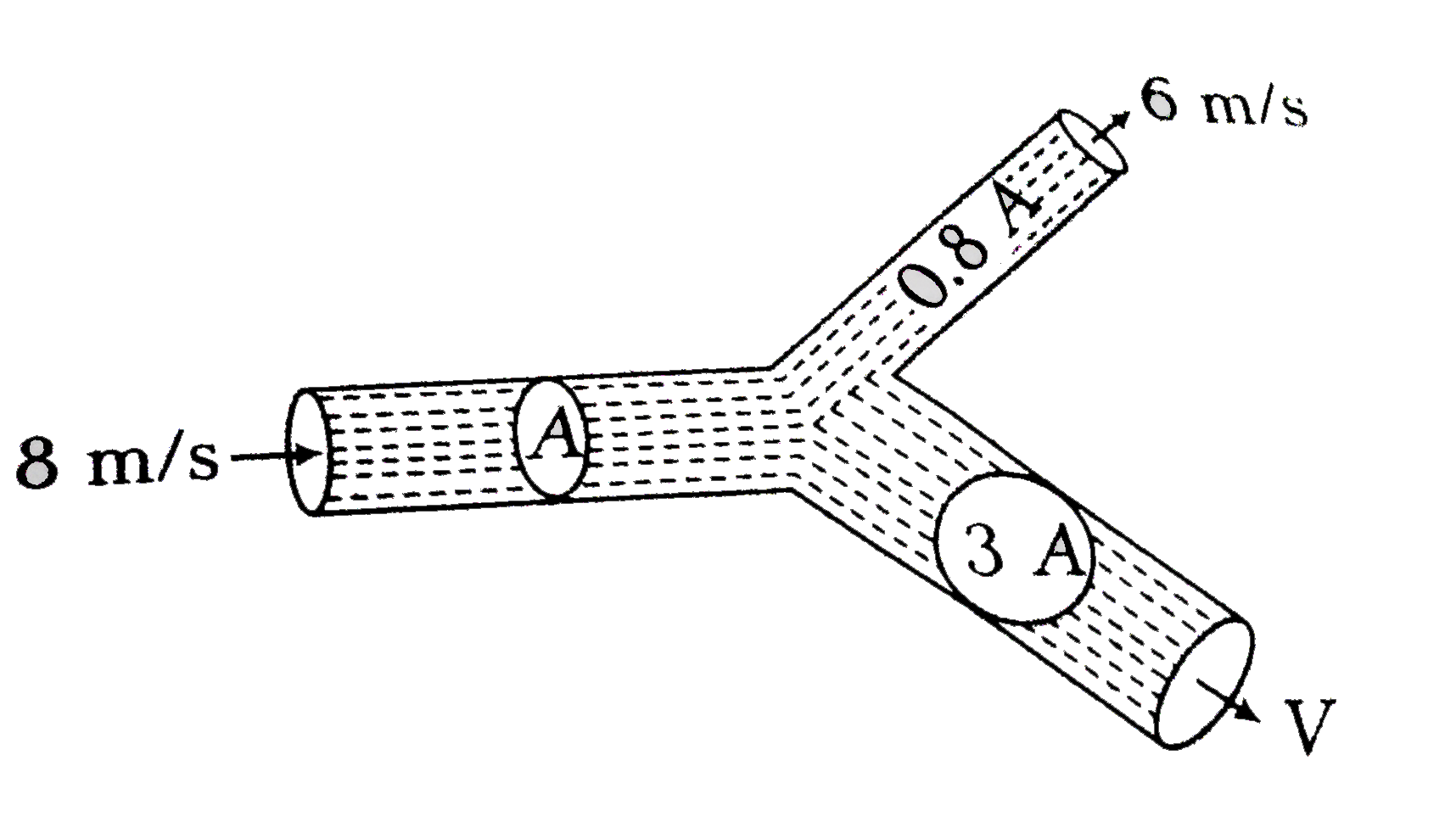
(a)1.1ms−1 (b)2.1ms−1
(c)3.1ms−1 (d)5.1ms−1
View SolutionA particle is moving with constant speed v in xy plane as shown in figure. The magnitude of its angular velocity about point O is

View SolutionA non viscous inconpressible liquid is flowing from a horizontal pipe of non-uniform cross section as shown, Choose the correct option
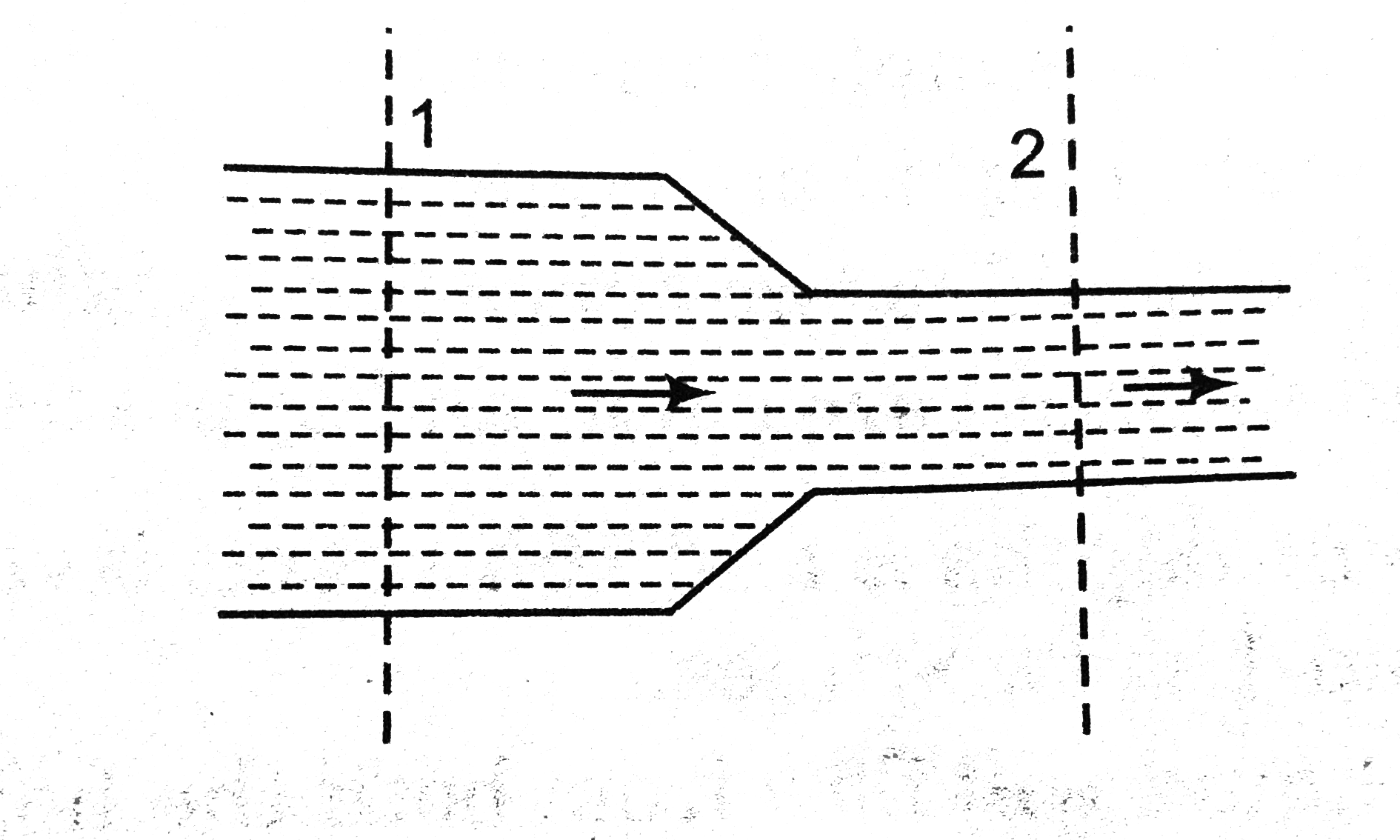
View SolutionA current of I amperes is flowing through each of the bent wires as shown. Find the magnitude of magnetic field at O.
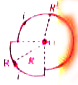
View SolutionIn given figure, current I is flowing through straight wire and divided equally in two loops as shown in the figure. The magnitude of magnetic field intensity at the center (O) is
View Solution