A parallel plate capacitor with liquid filled between the plates (dielectric constant of liquid, k=4)has capacitance 20μF. If the liquid is removed then capacitance of capacitor becomes
10μF
5μF
80μF
20μF
To solve the problem, we need to understand the relationship between the capacitance of a capacitor with a dielectric material and the capacitance without the dielectric.
1. Identify Given Values:
- Capacitance with dielectric (C_m) = 20 µF
- Dielectric constant (k) = 4
2. Use the Formula for Capacitance:
The capacitance of a capacitor with a dielectric is given by the formula:
Cm=k⋅C0
where:
- Cm is the capacitance with the dielectric,
- k is the dielectric constant,
- C0 is the capacitance without the dielectric.
3. Rearrange the Formula to Find C0:
To find the capacitance without the dielectric, rearrange the formula:
C0=Cmk
4. Substitute the Known Values:
Substitute the known values into the equation:
C0=20μF4
5. Calculate C0:
Perform the division:
C0=5μF
6. Conclusion:
The capacitance of the capacitor when the liquid is removed (without the dielectric) is 5μF.
Final Answer:
The capacitance of the capacitor becomes 5μF.
---
- Capacitance with dielectric (C_m) = 20 µF
- Dielectric constant (k) = 4
The capacitance of a capacitor with a dielectric is given by the formula:
Cm=k⋅C0
where:
- Cm is the capacitance with the dielectric,
- k is the dielectric constant,
- C0 is the capacitance without the dielectric.
To find the capacitance without the dielectric, rearrange the formula:
C0=Cmk
Substitute the known values into the equation:
C0=20μF4
Perform the division:
C0=5μF
The capacitance of the capacitor when the liquid is removed (without the dielectric) is 5μF.
The capacitance of the capacitor becomes 5μF.
Similar Questions
A parallel plate condenser with oil (dielectric constant 2) between the plates has capacitance C. If oil is removed, the capacitance of capacitor becomes
View SolutionThe capacitor shown has square plates of side L and has gap d between the photos. In the dielectric constant of the materiale of the slab is k , the capacitance of the capacitor is

View Solution
Knowledge Check
A parallel plate capacitor with air between the plates has a capacitance of 10 pF. The capacitance, if the distance bgetween the plates is reduced by half and the space between tehm is filled with a substance of dielectric constant 4 is
A80pFB96pFC100pFD120pFA parallel plate air capacitor has a capacitance C. When it is half filled with a dielectric of dielectric constant 5, the percentage increase in the capacitance will be
A400%B66.6%C33.3%D200%
The two plates of a parallel plate capacitor are 4mm apart. A slab of dielectric constant 3 and thickness 3mm is introduced between the plates is so adjusted that the capacitance of the capacitor becomes 23rd of its original value. What is the new distance between the plates ?
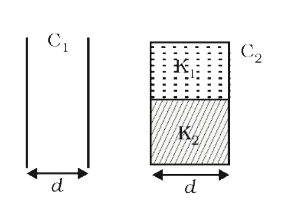
View SolutionYou are given an air filled parallel plate capacitor c1. The space between its plates is now filled with slabs of dielectric constant k1andk2 as shown in c2. Find the capacitances of the capacitor c2 if area of the plates is A distance between the plates is d.
View SolutionTo reduce the capacitance of parallel plate capacitor, the space between the plate is
View SolutionA parallel plate capacitor, with plate area A and plate separation d, is filled with a dielectric slabe as shown. What is the capacitance of the arrangement ?
View SolutionIn a parallel-plate capacitor, the region between the plates is filled by a dielectric slab. The capacitor is connected to a cell and the slab is taken out. Then
View SolutionA parallel plate capacitor with air between the plates has a capacitance of 8 pF.(1pF=10−12F) What will be the capacitance if the distance between the plates is reduced by half and the space between them is filled with a substance of dielectric constant 6 ?
View Solution