A block of mass m is kept over another block of mass 2m. Coefficient of friction between two blocks is and that of between lower blood from the horizontal surface is zero. A horizontal force is applied on the block of mass . Acceleration of lower block is
To solve the problem, we will analyze the forces acting on both blocks and apply Newton's laws of motion.
1. Identify the Forces:
- The lower block (mass = 2m) is subjected to a horizontal force F=43μmg.
- The upper block (mass = m) experiences a frictional force due to the lower block.
2. Determine the Maximum Frictional Force:
- The maximum static frictional force fmax between the two blocks is given by:
fmax=μ⋅m⋅g
3. Assume Both Blocks Move Together:
- If both blocks move together, the total mass being accelerated is 2m+m=3m.
- The acceleration a of both blocks can be calculated using Newton's second law:
F=(2m+m)⋅a⟹a=F3m
4. Substituting the Force:
- Substitute F=43μmg into the equation for acceleration:
a=43μmg3m=49μg
5. Check the Friction Condition:
- The frictional force acting on the upper block (mass = m) must be equal to the force required to accelerate it:
f=m⋅a=m⋅49μg=49μmg
- This frictional force must not exceed the maximum static friction:
f≤fmax⟹49μmg≤μmg
- This condition holds true, confirming that both blocks can indeed move together.
6. Conclusion:
- Since both blocks move together with the same acceleration, the acceleration of the lower block (mass = 2m) is:
a=49μg
Final Answer:
The acceleration of the lower block is 49μg.
---
- The lower block (mass = 2m) is subjected to a horizontal force F=43μmg.
- The upper block (mass = m) experiences a frictional force due to the lower block.
- The maximum static frictional force fmax between the two blocks is given by:
fmax=μ⋅m⋅g
- If both blocks move together, the total mass being accelerated is 2m+m=3m.
- The acceleration a of both blocks can be calculated using Newton's second law:
F=(2m+m)⋅a⟹a=F3m
- Substitute F=43μmg into the equation for acceleration:
a=43μmg3m=49μg
- The frictional force acting on the upper block (mass = m) must be equal to the force required to accelerate it:
f=m⋅a=m⋅49μg=49μmg
- This frictional force must not exceed the maximum static friction:
f≤fmax⟹49μmg≤μmg
- This condition holds true, confirming that both blocks can indeed move together.
- Since both blocks move together with the same acceleration, the acceleration of the lower block (mass = 2m) is:
a=49μg
The acceleration of the lower block is 49μg.
Similar Questions
Two blocks of masses'm' and 'M' are arranged as shown in the figure. The coefficient of friction between the two blocks is ' μ ', where as between the lower block and the horizontal surface is zero. Find the force 'F' to be applied on the upper block, for the system to be under equilibrium ?

View SolutionA block of mass m is kept on an another block of mass M. The coefficient of friction between the blocks varies as μ=(μ0+kx) while friction between lower block and ground is zero. A time varying force F = 10t is applied horizontally on the upper block. Find time t0 when relative motion will start between the blocks. (x is relative displacement between the blocks.)
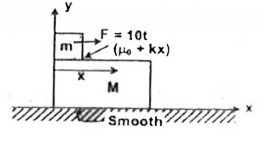
View Solution
Knowledge Check
The coefficient of static friction between the two blocks shown in figure is μ and the table is smooth. What maximum horizontal forced F can be applied to he block of mass M so that the block move together?
 A0.15mgB0.05mgC0.1mgD0.45mg
A0.15mgB0.05mgC0.1mgD0.45mg
A block of massm is placed on another block of mass M which itself is lying on a horizontal surface .The coefficient of friction between two blocks is μ1and that between the block of mass M and horizontal surfece is μ2 What maximum horizontal force can be applied to the lower block move without separation?

View SolutionA small block of mass 'm' is placed on a plank of mass 'M'. The block is connected to plank with the help of a light string passing over a light smooth pulley as shown in figure. The co-efficient of static friction between the block and plank is μ.
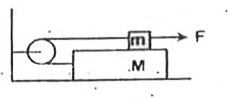
The co-efficient of friction between the plank and the horizontal surface is zero. What maximum horizontal force F applied on the block of mass m can make the block and plank not to slide relatively?
View SolutionThe block of mass M and are arrenged as the situation in fig is shown.The coefficient of friction between two block is μand that between the bigger block and the ground is μ find the acceleration of the block .
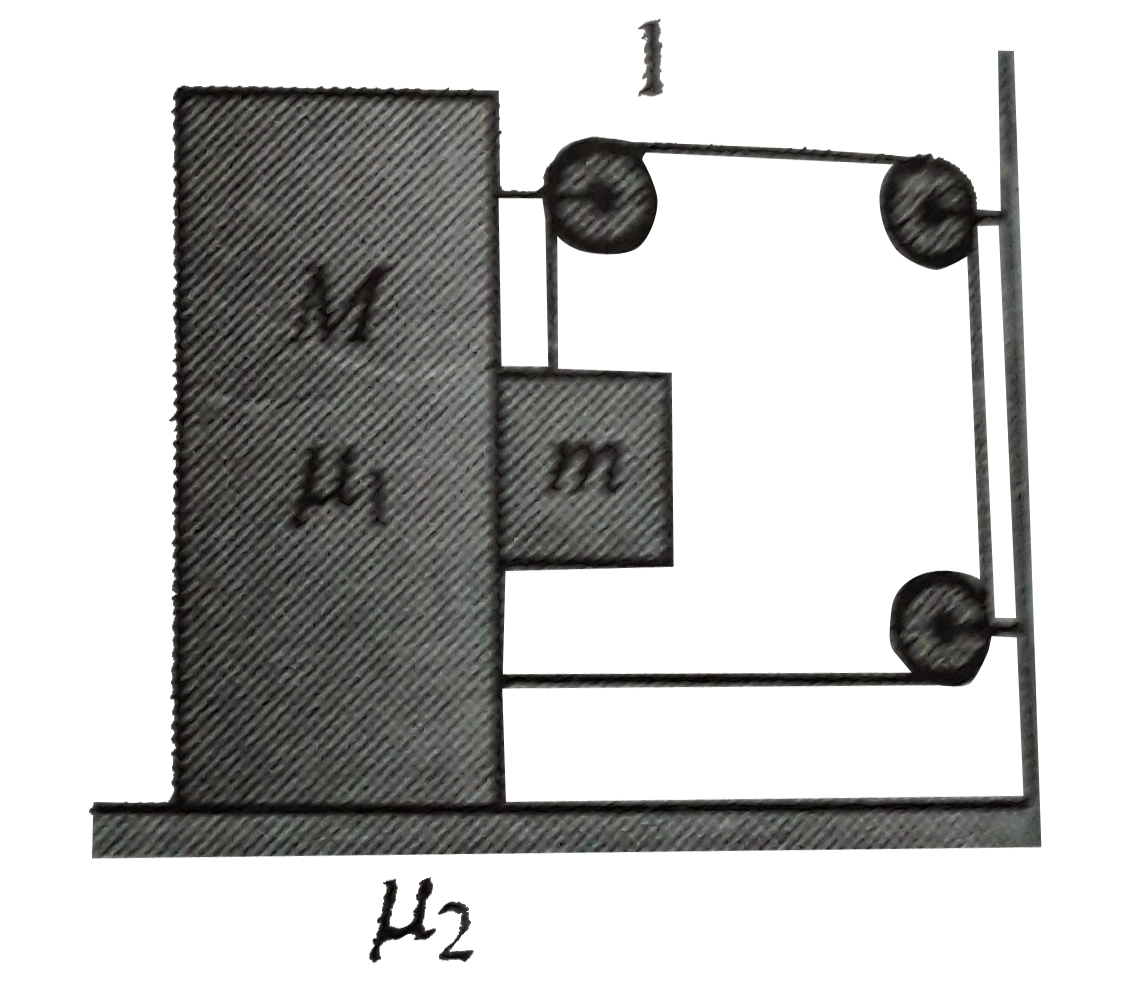
View SolutionA block of mass M is in contact with a cart of mass M. The coefficient of static friction between block and cart is μ . To prevent the block from sliding on cart, acceleration a should be
View SolutionThe coefficient of static friction between the two blocks shown in figure is μ and the table is smooth. What maximum horizontal forced F can be applied to he block of mass M so that the block move together?

View SolutionA block A of mass m kg lies on a block B of mass m kg. B in turn lies on smooth horizontal plane. The coefficient of friction between A and B is μ. Both the blocks are initially at rest. A horizontal force F is applied to lower block B at t = 0 till the lower block B undergoes a displacement of magnitude L. Match the statements in Table-1 with the results in Table-2.

View SolutionA block of mass m is placed on another block of mass M lying on a smooth horizontal surface as shown in the figure. The co-efficient of friction between the blocks is μ. Find the maximum horizontal force F (in Newton) that can be applied to the block M so that the blocks together with same acceleration? (M=3kg,m=2kg,μ=0.1,g=10m/s2)

View Solution
