A block of mass M is in contact with a cart of mass M. The coefficient of static friction between block and cart is μ . To prevent the block from sliding on cart, acceleration a should be
a>mg(m+M)μ
a≥gμ
a<gμ
a<mgMμ
The correct Answer is:b
To solve the problem, we need to determine the condition under which the block of mass M does not slide on the cart of mass M when the cart is accelerating with an acceleration a.
1. Identify Forces Acting on the Block:
- The block experiences a gravitational force downward, which is Mg.
- It also experiences a normal force N exerted by the cart, acting upward.
- When the cart accelerates, a pseudo force acts on the block in the opposite direction of the acceleration of the cart. This pseudo force is given by Fpseudo=Ma.
2. Static Friction Force:
- The static friction force Fs between the block and the cart must be sufficient to prevent the block from sliding. The maximum static friction force can be expressed as:
Fs≤μN
- Here, μ is the coefficient of static friction, and N is the normal force. Since the block is not moving vertically, the normal force N equals the weight of the block:
N=Mg
- Therefore, the maximum static friction force becomes:
Fs≤μMg
3. Setting Up the Equation:
- For the block to not slide, the static friction force must be equal to the pseudo force acting on the block:
Fs=Ma
- Substituting the expression for maximum static friction, we get:
Ma≤μMg
4. Solving for Acceleration a:
- Dividing both sides of the inequality by M (assuming M≠0):
a≤μg
- This implies that to prevent the block from sliding, the acceleration a of the cart must satisfy:
a≤μg
5. Conclusion:
- The condition for the block not to slide on the cart is:
a≤μg
Final Answer:
To prevent the block from sliding on the cart, the acceleration a should be:
a≤μg
- The block experiences a gravitational force downward, which is Mg.
- It also experiences a normal force N exerted by the cart, acting upward.
- When the cart accelerates, a pseudo force acts on the block in the opposite direction of the acceleration of the cart. This pseudo force is given by Fpseudo=Ma.
- The static friction force Fs between the block and the cart must be sufficient to prevent the block from sliding. The maximum static friction force can be expressed as:
Fs≤μN
- Here, μ is the coefficient of static friction, and N is the normal force. Since the block is not moving vertically, the normal force N equals the weight of the block:
N=Mg
- Therefore, the maximum static friction force becomes:
Fs≤μMg
- For the block to not slide, the static friction force must be equal to the pseudo force acting on the block:
Fs=Ma
- Substituting the expression for maximum static friction, we get:
Ma≤μMg
- Dividing both sides of the inequality by M (assuming M≠0):
a≤μg
- This implies that to prevent the block from sliding, the acceleration a of the cart must satisfy:
a≤μg
- The condition for the block not to slide on the cart is:
a≤μg
To prevent the block from sliding on the cart, the acceleration a should be:
a≤μg
Topper's Solved these Questions
Similar Questions
A block of mass m is in contact with the cart C as shown in The coefficient of static friction between the block and the cart is μ The acceleration a of the cart that will prevent the block from falling satisfies
 .
.
View SolutionA block of mass m is in contact with the cart C as shown in figure -
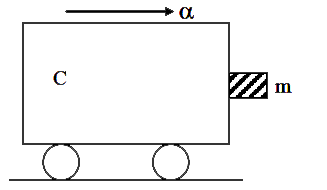
The coefficient of static friction between the block and the cart is μ , The accelertion α of the cart that will prevent the block from failing satisfies -
View SolutionA cart of mass M has a block of mass m in contact with it as shown in the figure-2.133. The coefficient of friction between the block and the cart is μ. What is the minimum acceleration of the cart so that the block m does not fall ?

View Solution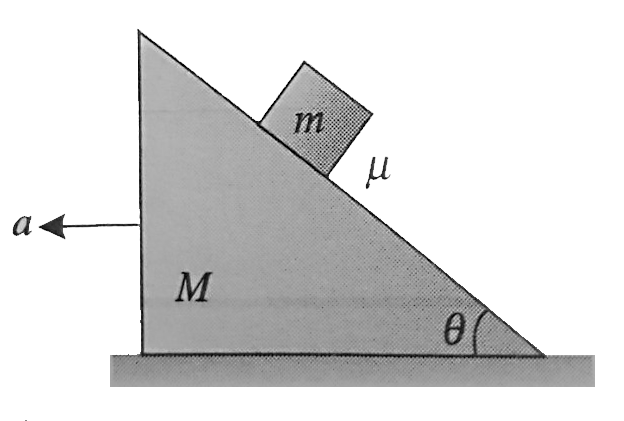
A block of mass m is at rest relative to the stationary wedge of mass M. The coefficient of friction between block and wedge is μ. The wedge is now pulled horizontally with acceleration a as shown in figure. Then the minimum magnitude of a for the friction between block and wedge to be zero is:
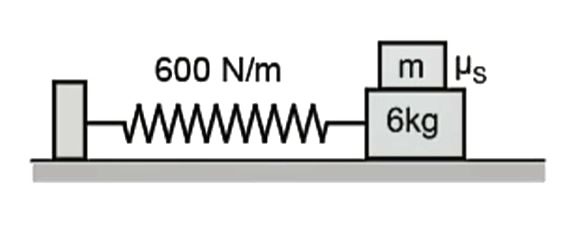
View SolutionA block of mass m is placed on the top of a 6kg cart such that the time period of the system is 0.75 s assuming there is no slipping. If the cart is displaced by 50 mm from its equilibrium position and released, then the coefficient of static friction μs between block and cart is just sufficient to prevent the block from sliding. The value of m and μs respectively are (Take g=9.8m/s2)
View SolutionA block of mass 2 kg is at rest on a floor . The coefficient of static friction between block and the floor is 0.54. A horizonatl force of 2.8 N is applied to the block . What should be the frictional force between the block and the floor ? ( take , g=10m/s2)
View SolutionA block of mass M is kept on as rough horizontal surface. The coefficient of static frictionbetween the block and the surface is μ. The block is to be pulled by applying a force to it. What minimum force is needed to slide the block? In which direction should this force act?
View SolutionA block of mass M is kept on as rough horizontal surface. The coefficient of static friction between the block and the surface is μ. The block is to be pulled by applying a force to it. What minimum force is needed to slide the block? In which direction should this force act?
View SolutionA block of mass 1 kg is placed on a truck which accelerates with acceleration 5ms−2. The coefficient of static friction between the block and truck is 0.6. The frictional force acting on the block is
View SolutionA block of mass'm' is resting on the floor of a lift. The coefficient of friction between the block and the floor is μ. When the lift is falling freely, the limiting frictional force between block and surface is
View Solution
