A block of mass m is connected with another block of mass 2m kept on a rough horizontal table by means of an ideal spring of spring constant K and a massless string as shown in the figure. The minimum coefficient of friction between the block of mass 2m and the table so that the block does not slide, when block of mass m is suddenly released, is
14
12
1
34
To solve the problem, we need to analyze the forces acting on the blocks when the block of mass m is suddenly released.
1. Identify the Forces Acting on the Blocks:
- For the block of mass m:
- Weight Wm=mg acting downwards.
- Tension T in the string acting towards the block of mass 2m.
- For the block of mass 2m:
- Weight W2m=2mg acting downwards.
- Normal force N acting upwards, equal to the weight 2mg.
- Frictional force f acting to the left (opposite to the direction of tension) which is given by f=μN.
2. Set Up the Equation for Tension:
- When the block of mass m is released, it will exert a tension T on the block of mass 2m.
- The tension T can be expressed as:
T=mg
- The frictional force f must be equal to the tension for the block of mass 2m to not slide:
f=T
3. Express the Frictional Force:
- The frictional force is given by:
f=μN
- Since N=2mg (the normal force acting on the block of mass 2m):
f=μ(2mg)
4. Set the Two Expressions for Friction Equal:
- Setting the expressions for f equal gives:
mg=μ(2mg)
5. Solve for the Coefficient of Friction μ:
- Cancel mg from both sides (assuming m≠0):
1=2μ
- Rearranging gives:
μ=12
Final Answer:
The minimum coefficient of friction μ required between the block of mass 2m and the table so that the block does not slide is:
μ=12
- For the block of mass m:
- Weight Wm=mg acting downwards.
- Tension T in the string acting towards the block of mass 2m.
- For the block of mass 2m:
- Weight W2m=2mg acting downwards.
- Normal force N acting upwards, equal to the weight 2mg.
- Frictional force f acting to the left (opposite to the direction of tension) which is given by f=μN.
- When the block of mass m is released, it will exert a tension T on the block of mass 2m.
- The tension T can be expressed as:
T=mg
- The frictional force f must be equal to the tension for the block of mass 2m to not slide:
f=T
- The frictional force is given by:
f=μN
- Since N=2mg (the normal force acting on the block of mass 2m):
f=μ(2mg)
- Setting the expressions for f equal gives:
mg=μ(2mg)
- Cancel mg from both sides (assuming m≠0):
1=2μ
- Rearranging gives:
μ=12
The minimum coefficient of friction μ required between the block of mass 2m and the table so that the block does not slide is:
μ=12
Similar Questions
A block of mass m is connected to another .block of mass M by a massless spring of spring constant k. A constant force f starts action as shown in figure, then:

View SolutionA cart of mass M has a block of mass m in contact with it as shown in the figure-2.133. The coefficient of friction between the block and the cart is μ. What is the minimum acceleration of the cart so that the block m does not fall ?

View SolutionA small block of mass 2 kg is placed on a bigger block of mass 4 kg which is attached to horizontal spring of spring constant K=500N/m as shown in figure, coefficient of friction between block is 0.2 .Maximum amplitude of system so that there is no relative slipping between blocks.
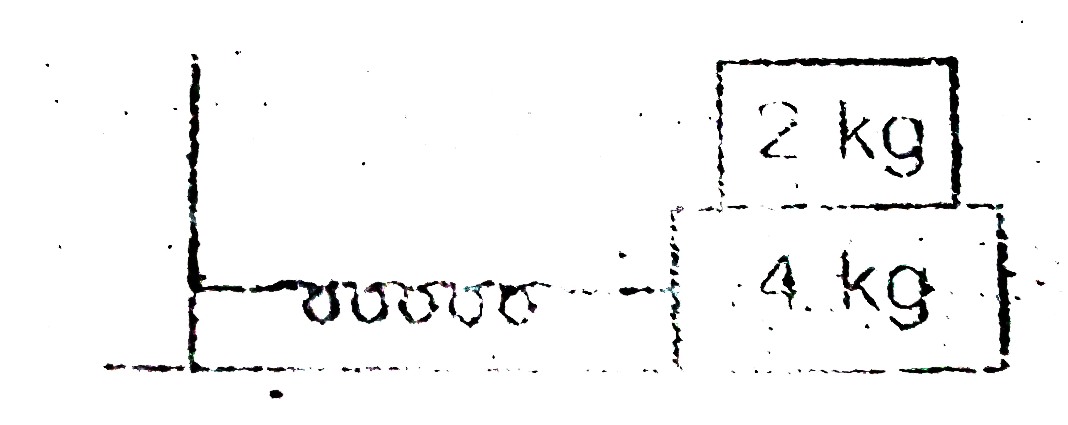
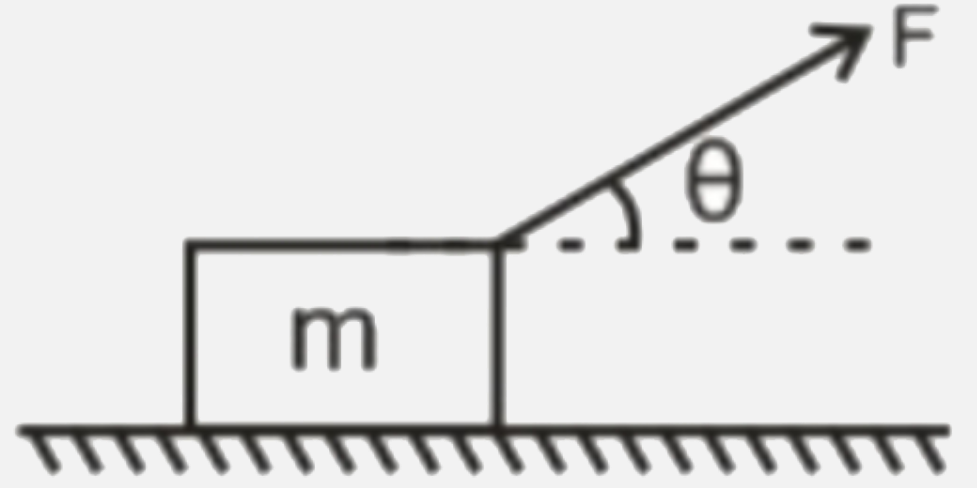
View SolutionA wooden block of mass m resting on a rough horizontal table is pulled by a force F as shown in the figure. If μ is the coefficient of friction between block and table, its acceleration will be
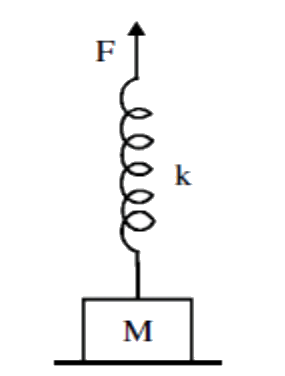
View SolutionA block of mass m is kept on a rough horizontal surface and is attached with a massless spring of force constant k. The minimum constant force applied on the other end of the spring of lift the block is
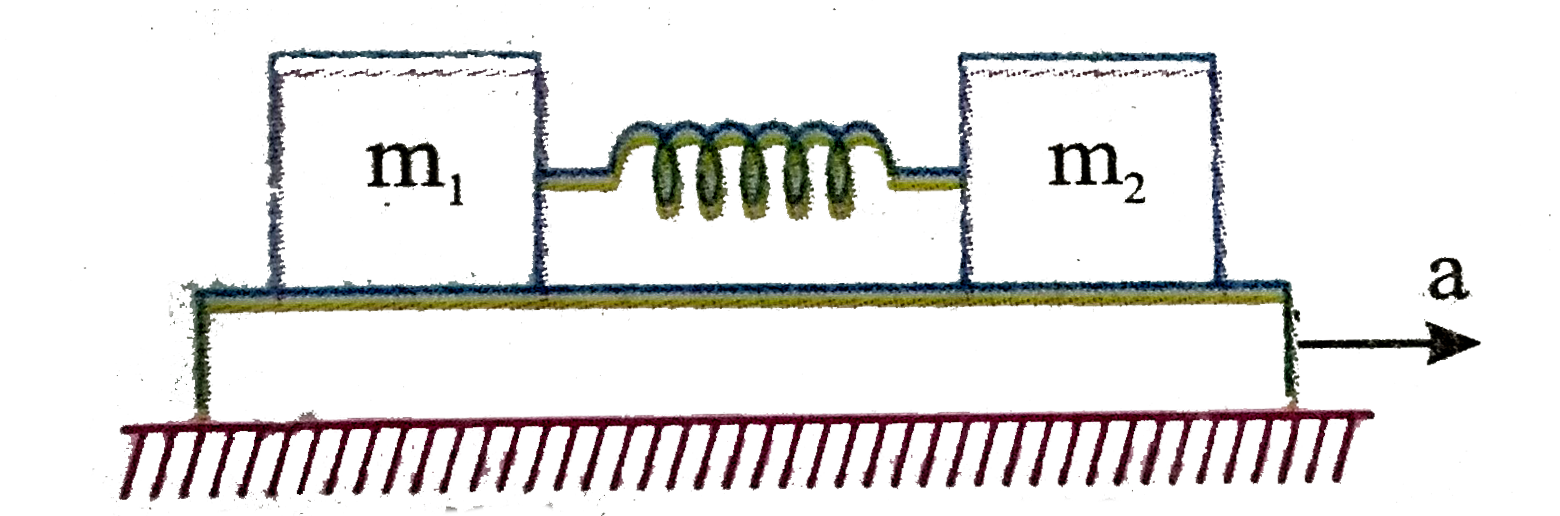
View SolutionTwo block of masses m1 and m2 are connected with a massless unstretched spring and placed over a plank moving with an acceleration 'a' as shown in figure. The coefficient of friction between the blocks and platform is μ
View SolutionA block of mass m kept on rough horizontal turn table at a distance x from the centre. If the coefficient of friction between the table and block is μ then maximum speed of point P on turn table so that the block does not slip is

View SolutionTwo blocks of masses m1 and m2 are connected through a massless inextensible string .A block of mass m1 is placed at the fixed rigid inclined surface while the block of mass m2 hanging at the other end of the string which is passing through a fixed massless frictionless pulley shown in figure The coefficient of static friction between the block and the inclined plane is 0.8 The system of masses m1 and m2 released from rest
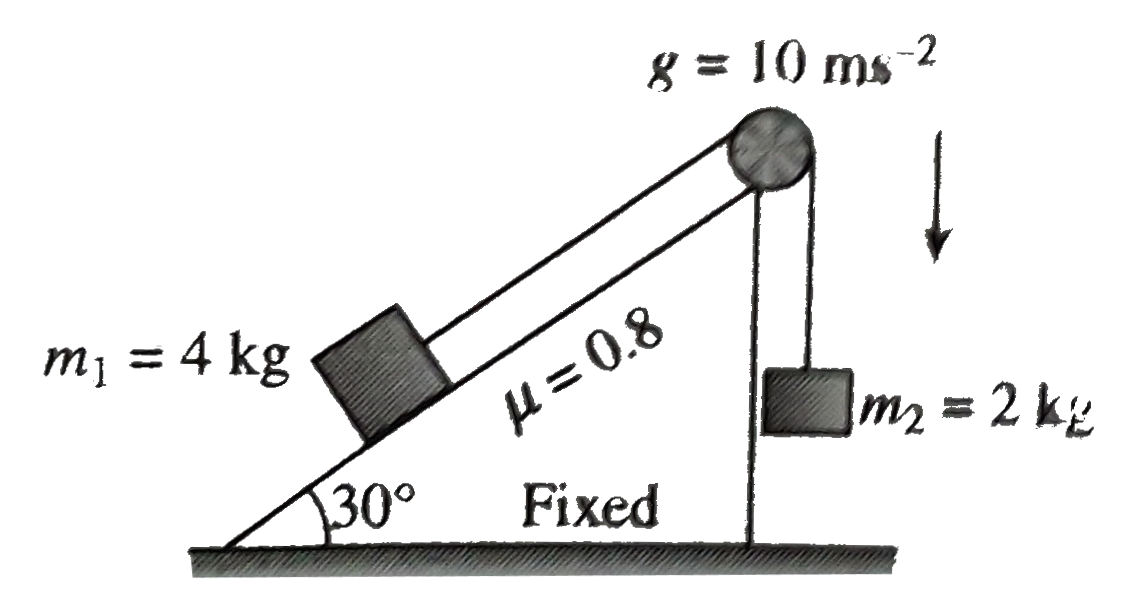
View SolutionTwo block of same mass'm' are joined with an dideal spring of spring constant k and sept on a rough surface as shown in figure. The spring is initially unstretched and coefficient of friction between the blocks and horizontal surface is μ and 2μ respectively. What should be the maximum speed of block 'A' such that the block 'B' does not move ?
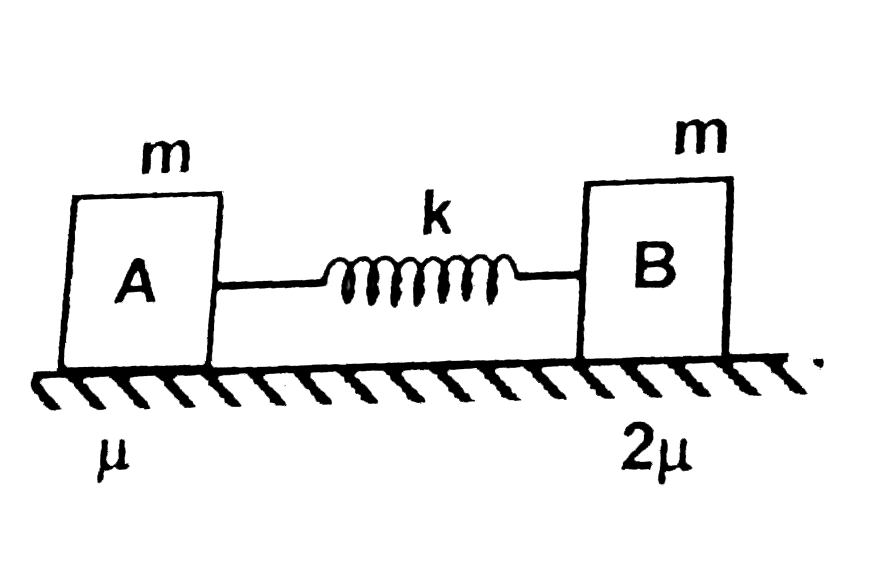
View SolutionA block of mass m is kept on a horizontal table. If the static friction coefficient is μ., find the frictional force acting on the block.
View Solution
