A force →F=(3ˆi+4ˆj) N is acting on a particle. Work done by the force is zero, when particle is moving on the line 2y+Px=2, the value of P is
12
32
52
43
To solve the problem step by step, we need to determine the value of P such that the work done by the force →F=3^i+4^j N is zero when the particle is moving along the line given by the equation 2y+Px=2.
Step 1: Understand the Work Done by the Force
The work done W by a force →F when a particle moves through a displacement d→r is given by the dot product:
W=∫→F⋅d→r
For the force →F=3^i+4^j, we can express the displacement d→r as dx^i+dy^j.
Step 2: Calculate the Dot Product
The dot product →F⋅d→r becomes:
→F⋅d→r=(3^i+4^j)⋅(dx^i+dy^j)=3dx+4dy
Step 3: Analyze the Line Equation
The line equation is given as:
2y+Px=2
We can rearrange this to express y in terms of x:
2y=2−Px⟹y=1−P2x
Step 4: Differentiate the Line Equation
To find dy in terms of dx, we differentiate y:
dy=−P2dx
Step 5: Substitute dy into the Work Done Expression
Now substitute dy into the expression for work done:
W=∫(3dx+4dy)=∫(3dx+4(−P2dx))
This simplifies to:
W=∫(3dx−2Pdx)=∫(3−2P)dx
Step 6: Set the Work Done to Zero
According to the problem, the work done is zero:
3−2P=0
Step 7: Solve for P
Now, solve for P:
2P=3⟹P=32
Conclusion
Thus, the value of P is 32.
The work done W by a force →F when a particle moves through a displacement d→r is given by the dot product:
W=∫→F⋅d→r
For the force →F=3^i+4^j, we can express the displacement d→r as dx^i+dy^j.
The dot product →F⋅d→r becomes:
→F⋅d→r=(3^i+4^j)⋅(dx^i+dy^j)=3dx+4dy
The line equation is given as:
2y+Px=2
We can rearrange this to express y in terms of x:
2y=2−Px⟹y=1−P2x
To find dy in terms of dx, we differentiate y:
dy=−P2dx
Now substitute dy into the expression for work done:
W=∫(3dx+4dy)=∫(3dx+4(−P2dx))
This simplifies to:
W=∫(3dx−2Pdx)=∫(3−2P)dx
According to the problem, the work done is zero:
3−2P=0
Now, solve for P:
2P=3⟹P=32
Thus, the value of P is 32.
Similar Questions
Force acting on a particale is (2ˆi+3ˆj)N. Work done by this force is zero, when the particle is moved on the line 3y+kx=5. Here value of k is (Work done W=→F.→d)
View SolutionForce acting on a particale is (2ˆi+3ˆj)N. Work done by this force is zero, when the particle is moved on the line 3y+kx=5. Here value of k is (Work done W=→F.→d)
View SolutionA force →F=(3xy−5z)ˆj+4zˆk is applied on a particle. The work done by the force when the particle moves from point (0,0,0) to point (2,4,0) as shown in figure.
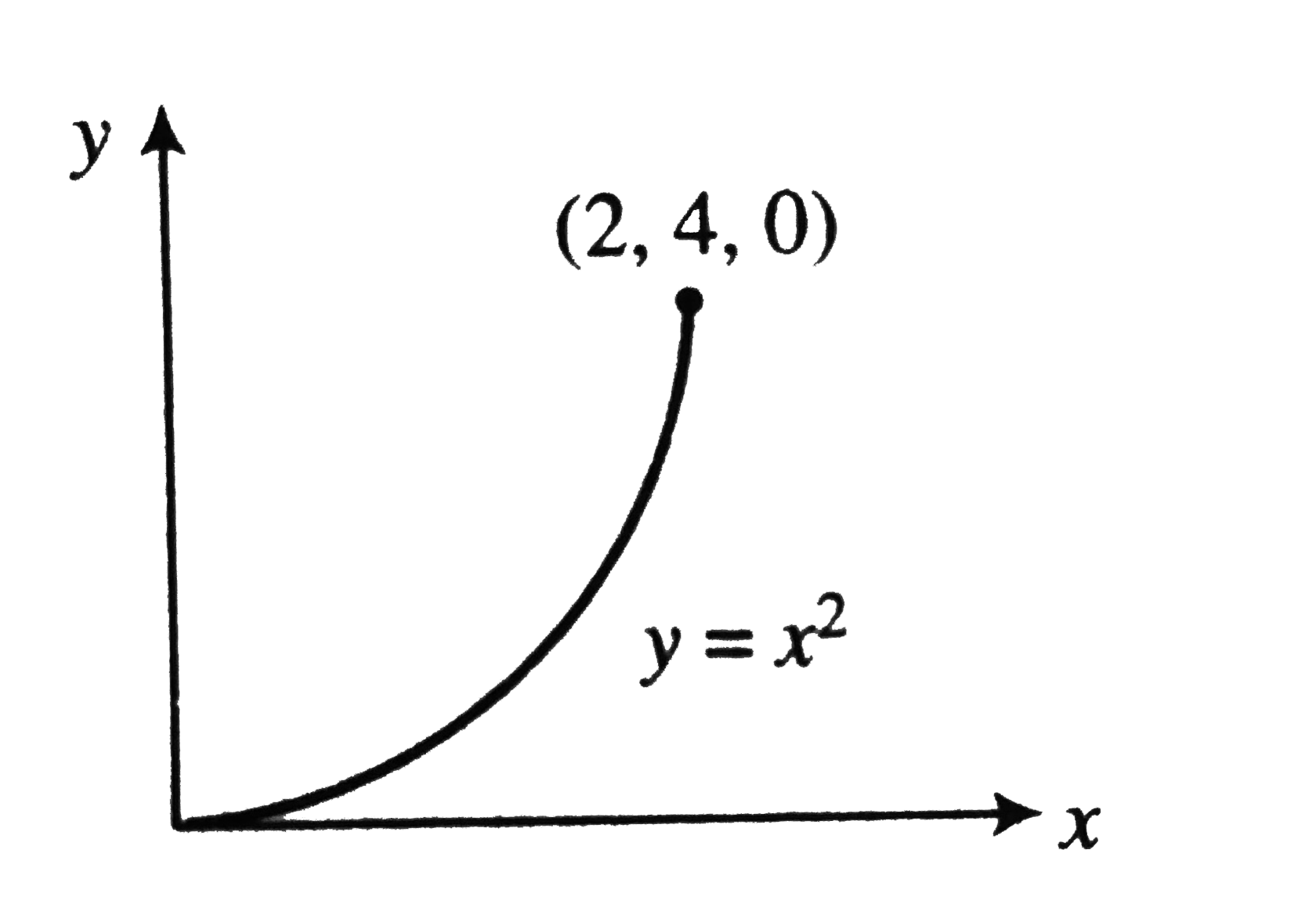 View Solution
View SolutionForce acting on a pasrticle is →F=(αyˆi+βxyˆj). Find the work done by this force, when pasrticle is moved alolng the line 2x=3y from origin to the point (3,2) {take quantities in SI units and α=1,β=1}
View SolutionA force of →F=2xˆi+2ˆj+3z2ˆkN is acting on a particle. Find the work done by this force in displacing the body from (1,2,3)m to (3,6,1)m.
View SolutionA force F=(2ˆi−ˆj+4ˆk)N displaces a particle upto d=(3ˆi+2ˆj+ˆk)m. Work done by the force is
View SolutionA force (ˆi−2ˆj+3ˆk) acts on a particle lying at origin. What is the torque acting on the particle about origin?
View SolutionA force (ˆi−2ˆj+3ˆk) acts on a particle lying at origin. What is the torque acting on the particle about the origin.
View SolutionA force →F=(4ˆi+5ˆj)N acts on a particle moving in XY plane. Starting from origin, the particle first goes along x-axis to the point (5.0) m and then parallel to the Y-axis to the point (5,4 m. The total work done by the force on the particle is
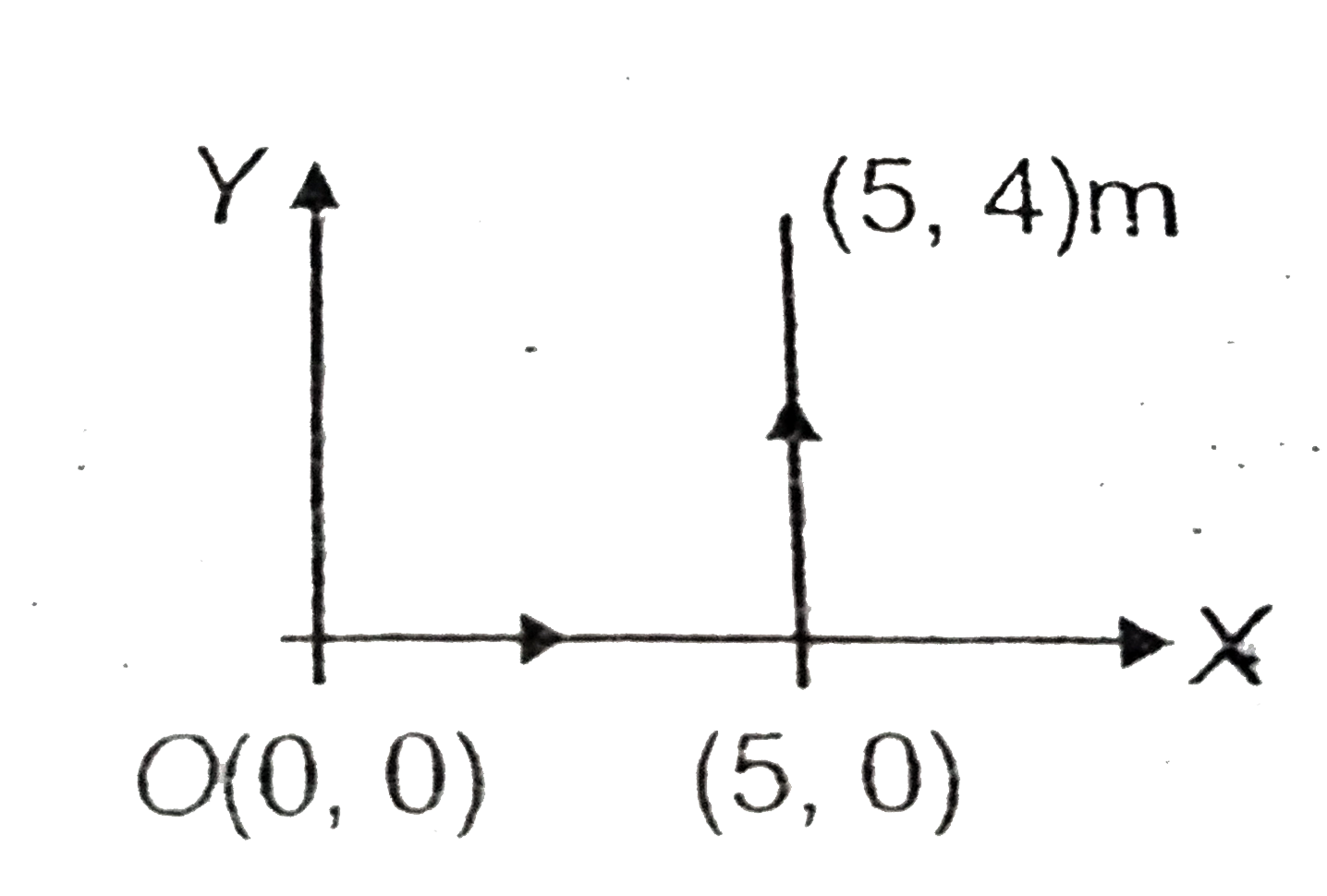 View Solution
View SolutionA force →F=(3ˆi+4ˆj)N is acting on a point mass m=(12)kg at a point A(2m,2m). Find the angular acceleration of the line OA at this instant.
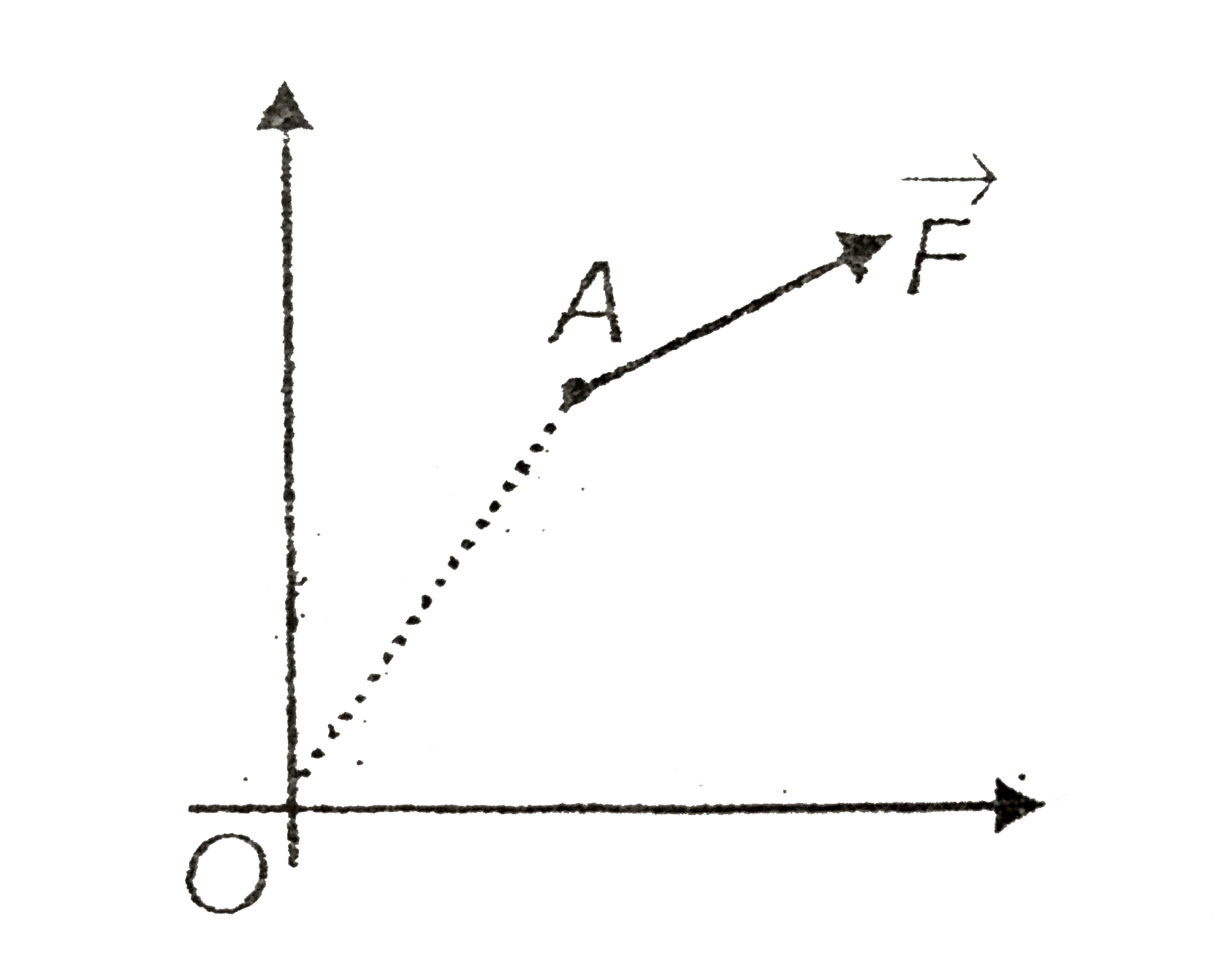 View Solution
View Solution

