Force acting on a pasrticle is →F=(αyˆi+βxyˆj). Find the work done by this force, when pasrticle is moved alolng the line 2x=3y from origin to the point (3,2) {take quantities in SI units and α=1,β=1}
The correct Answer is:7
To find the work done by the force →F=(αy^i+βxy^j) as the particle moves along the line 2x=3y from the origin to the point (3,2), we will follow these steps:
Step 1: Define the Force
Given:
α=1,β=1
Thus, the force can be expressed as:
→F=(y^i+xy^j)
Step 2: Parameterize the Path
The line 2x=3y can be rearranged to express y in terms of x:
y=23x
We will move from the origin (0,0) to the point (3,2).
Step 3: Express dy in terms of dx
Differentiating y=23x:
dy=23dx
Step 4: Write the Displacement Vector
The small displacement vector d→r is given by:
d→r=dx^i+dy^j=dx^i+23dx^j=(dx^i+23dx^j)
Step 5: Calculate the Work Done
The work done dW by the force along the path is given by the dot product:
dW=→F⋅d→r
Substituting →F and d→r:
dW=(y^i+xy^j)⋅(dx^i+23dx^j)
Calculating the dot product:
dW=ydx+xy(23dx)=ydx+23xydx
Factoring out dx:
dW=(y+23xy)dx
Step 6: Substitute y in terms of x
Substituting y=23x:
dW=(23x+23x⋅23x)dx=(23x+49x2)dx
Step 7: Integrate to Find Total Work Done
Now, we integrate from x=0 to x=3:
W=∫30(23x+49x2)dx
Calculating the integral:
W=∫3023xdx+∫3049x2dx
Calculating each part:
1. ∫23xdx=23⋅x22=13x2
2. ∫49x2dx=49⋅x33=427x3
Evaluating from 0 to 3:
W=(13(32)+427(33))−(13(02)+427(03))
Calculating:
W=(13(9)+427(27))=3+4=7Joules
Final Answer
The work done by the force is W=7J.
---
Given:
α=1,β=1
Thus, the force can be expressed as:
→F=(y^i+xy^j)
The line 2x=3y can be rearranged to express y in terms of x:
y=23x
We will move from the origin (0,0) to the point (3,2).
Differentiating y=23x:
dy=23dx
The small displacement vector d→r is given by:
d→r=dx^i+dy^j=dx^i+23dx^j=(dx^i+23dx^j)
The work done dW by the force along the path is given by the dot product:
dW=→F⋅d→r
Substituting →F and d→r:
dW=(y^i+xy^j)⋅(dx^i+23dx^j)
Calculating the dot product:
dW=ydx+xy(23dx)=ydx+23xydx
Factoring out dx:
dW=(y+23xy)dx
Substituting y=23x:
dW=(23x+23x⋅23x)dx=(23x+49x2)dx
Now, we integrate from x=0 to x=3:
W=∫30(23x+49x2)dx
Calculating the integral:
W=∫3023xdx+∫3049x2dx
Calculating each part:
1. ∫23xdx=23⋅x22=13x2
2. ∫49x2dx=49⋅x33=427x3
W=(13(32)+427(33))−(13(02)+427(03))
Calculating:
W=(13(9)+427(27))=3+4=7Joules
The work done by the force is W=7J.
Topper's Solved these Questions
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PART - II PHYSICS
106 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems
13 Videos
- TEST SERIESBOOK - RESONANCE ENGLISHCHAPTER - TEST SERIESEXERCISE - PHYSICS
130 Videos
Similar Questions
A force →F=(3ˆi+4ˆj) N is acting on a particle. Work done by the force is zero, when particle is moving on the line 2y+Px=2, the value of P is
View SolutionA force of →F=2xˆi+2ˆj+3z2ˆkN is acting on a particle. Find the work done by this force in displacing the body from (1,2,3)m to (3,6,1)m.
View Solution
Knowledge Check
A body constrained to move along y-axis is subjected to a constant force →F=−ˆi+2ˆj+3ˆkN. The work done by this force in moving the body a distance of 4 m along y-axis is
A4JB8 JC12JD24 J
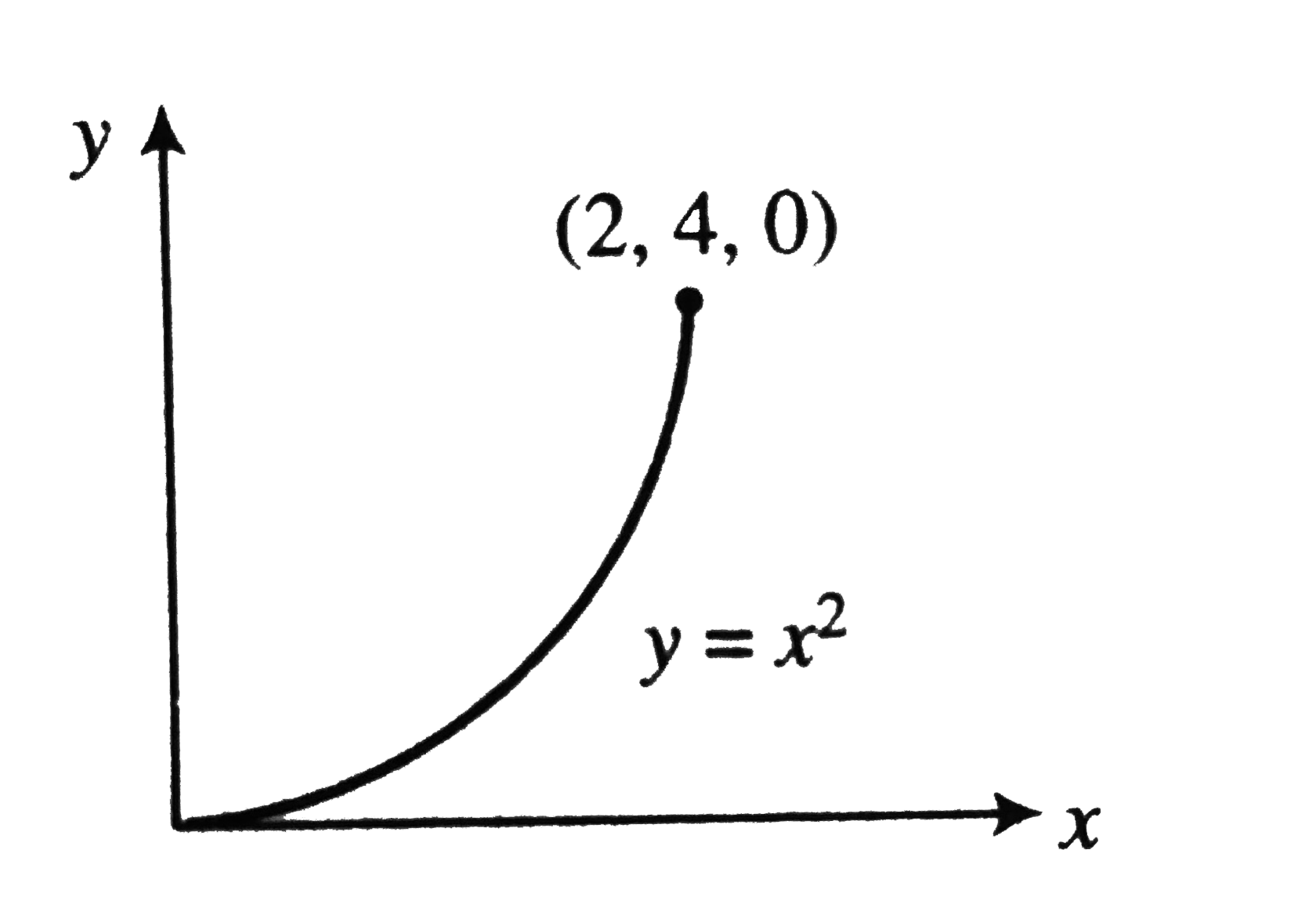
A force →F=(3xy−5z)ˆj+4zˆk is applied on a particle. The work done by the force when the particle moves from point (0,0,0) to point (2,4,0) as shown in figure.
View SolutionThe work done by the forces →F=2ˆi−ˆj−ˆk in moving an object along the vectors 3ˆi+2ˆj−5ˆk is:
View SolutionA force (3ˆi+4ˆj) newton acts on a boby and displaces it by (2ˆi+3ˆj) metre. The work done by the force is
View SolutionThe chrods of contact of the pair of tangents to the circle x2+y2=1 dravwm from any point on the line 2x+y=4 paas through the point (α,β) then find αandβ.
View SolutionA force →F=6xˆi+2yˆj displaces a body from →r1=3ˆi+8ˆj to →r2=5ˆi−4ˆj. Find the work done by the force.
View SolutionA body displaced from (1,1) to (2,2) along the line y=x under the force →F=xˆj+yˆi then find the work done by this force for above displacement. (all units are in S.I.)
View SolutionA body constrained to move along y-axis is subjected to a constant force →F=−ˆi+2ˆj+3ˆkN. The work done by this force in moving the body a distance of 4 m along y-axis is
View Solution
