A ball of mass 600 gm strikes a wall with a velocity of 5ms−1 at an angle 30∘ with the wall and rebounds with the same speed at the same angle with the wall. The change in momentum of the ball is, (in kg ms−1)
15
10
5
3
The correct Answer is:D
To solve the problem of finding the change in momentum of a ball that strikes a wall and rebounds, we can follow these steps:
Step 1: Understand the Given Data
- Mass of the ball, m=600g=0.6kg
- Initial velocity of the ball, v=5m/s
- Angle of incidence with the wall, θ=30∘
Step 2: Calculate the Components of Velocity
When the ball strikes the wall at an angle, we need to resolve its velocity into components:
- The horizontal component of the velocity (perpendicular to the wall) is given by:
vx=vcos(θ)
- The vertical component of the velocity (parallel to the wall) is given by:
vy=vsin(θ)
Step 3: Calculate the Horizontal Component
Substituting the values:
vx=5cos(30∘)
Using cos(30∘)=√32:
vx=5×√32=5√32m/s
Step 4: Calculate the Change in Momentum
The change in momentum is calculated using the formula:
ΔP=Pfinal−Pinitial
Since the ball rebounds with the same speed at the same angle, the horizontal momentum changes direction:
- Initial momentum in the x-direction:
Pinitial=mvx=0.6×5√32
- Final momentum in the x-direction (after rebounding):
Pfinal=−mvx=−0.6×5√32
Step 5: Calculate the Change in Momentum
Now substituting the values:
ΔP=Pfinal−Pinitial=−0.6×5√32−(0.6×5√32)
ΔP=−0.6×5√32+0.6×5√32=2×(0.6×5√32)
ΔP=2×0.6×5√32=0.6×5√3
Step 6: Calculate the Numerical Value
Using √3≈1.732:
ΔP=0.6×5×1.732=5.196kg m/s
Step 7: Finalize the Answer
The change in momentum is approximately 3kg m/s (as the cosine component simplifies the calculation).
Thus, the final answer is:
ΔP=3kg m/s
- Mass of the ball, m=600g=0.6kg
- Initial velocity of the ball, v=5m/s
- Angle of incidence with the wall, θ=30∘
When the ball strikes the wall at an angle, we need to resolve its velocity into components:
- The horizontal component of the velocity (perpendicular to the wall) is given by:
vx=vcos(θ)
- The vertical component of the velocity (parallel to the wall) is given by:
vy=vsin(θ)
Substituting the values:
vx=5cos(30∘)
Using cos(30∘)=√32:
vx=5×√32=5√32m/s
The change in momentum is calculated using the formula:
ΔP=Pfinal−Pinitial
Since the ball rebounds with the same speed at the same angle, the horizontal momentum changes direction:
- Initial momentum in the x-direction:
Pinitial=mvx=0.6×5√32
- Final momentum in the x-direction (after rebounding):
Pfinal=−mvx=−0.6×5√32
Now substituting the values:
ΔP=Pfinal−Pinitial=−0.6×5√32−(0.6×5√32)
ΔP=−0.6×5√32+0.6×5√32=2×(0.6×5√32)
ΔP=2×0.6×5√32=0.6×5√3
Using √3≈1.732:
ΔP=0.6×5×1.732=5.196kg m/s
The change in momentum is approximately 3kg m/s (as the cosine component simplifies the calculation).
ΔP=3kg m/s
Similar Questions
An object of m kg with speed of v ms−1 strikes a wall at an angle θ and rebounds at the same speed and same angle. Find the magnitude of change in the momentum of object.
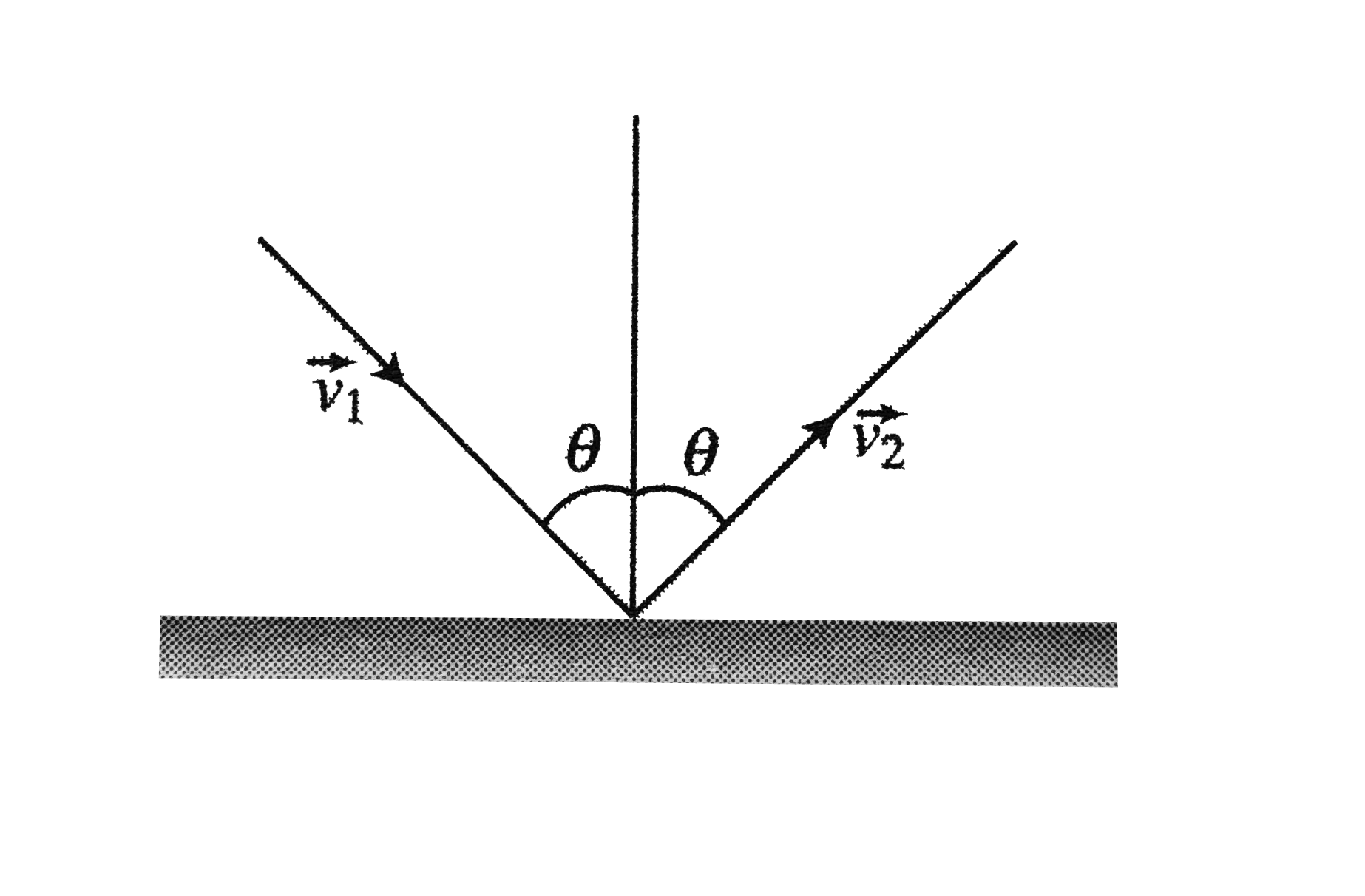
View SolutionAn object of m kg with speed of v ms−1 strikes a wall at an angle θ and rebounds at the same speed and same angle. Find the magnitude of change in the momentum of object.

View Solution
Knowledge Check
A ball of mass m strikes a rigid walJ with speed u and rebounds with the same speed. The impulse imparted to the ball by the wall is
 Amu sin30∘tB2mu sin30∘tCmu cos30∘tD2mu cos30∘t
Amu sin30∘tB2mu sin30∘tCmu cos30∘tD2mu cos30∘tA ball of mass m strikes a rigid walJ with speed u and rebounds with the same speed. The impulse imparted to the ball by the wall is
A2muBmuCzeroD−2mu
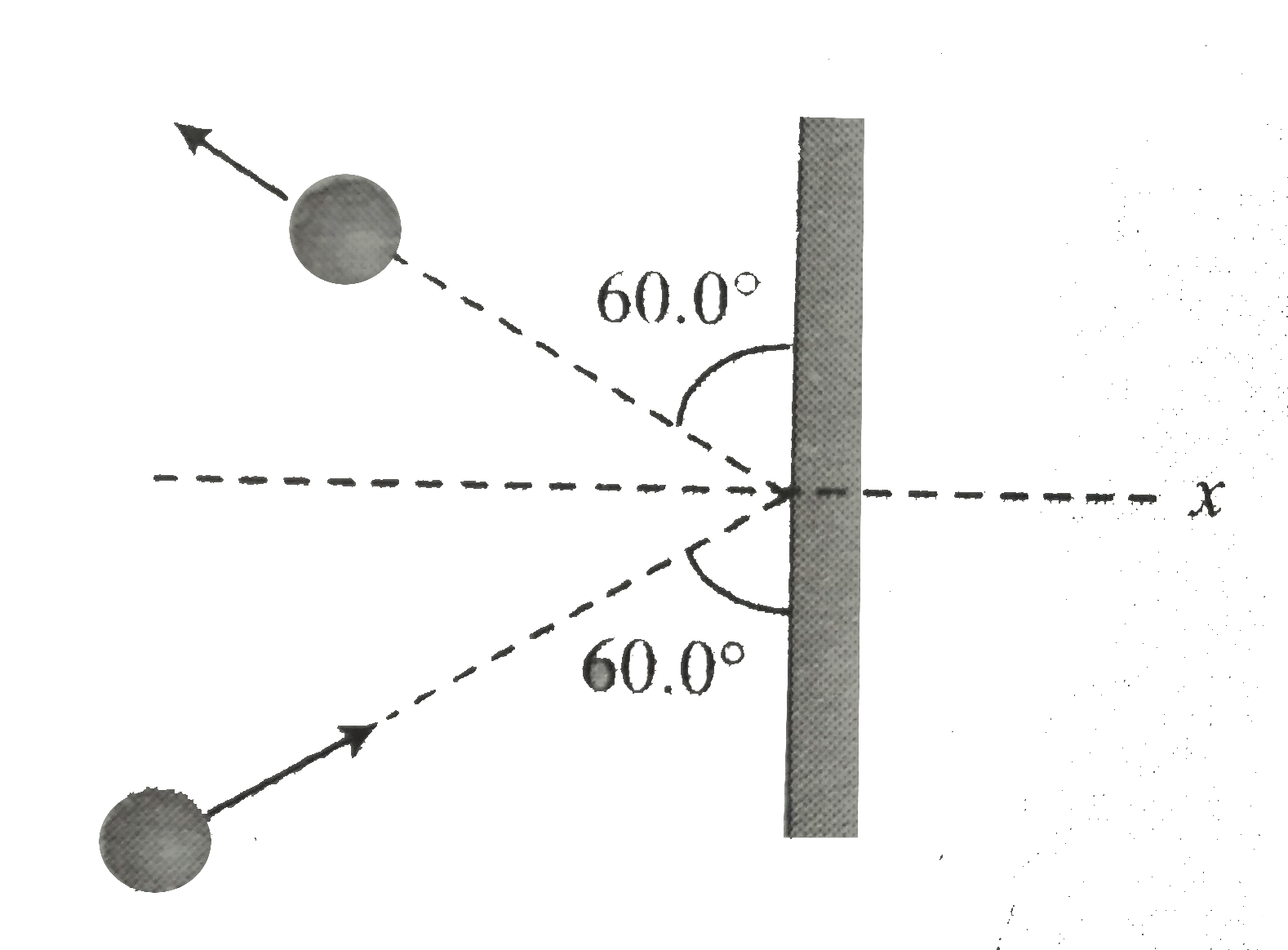
A 3-kg steel ball strikes a wall with a speed of 10.0ms−1 at an angle of 60.0∘ with the surfaces of the wall. The ball bounces off with the same speed and same angle. If the ball was in contact with the wall for 0.2s, find the average force exerted by the wall on the ball.
View SolutionA ball strikes a wall with a velocity →u at an angle θ with the normal to the wall surface. and rebounds from it at an angle β with the surface. Then
View SolutionA 1 kg particle strikes a wall with velocity 1 m/s at an angle of 60o with the wall and reflects at the same angle. If it remains in contact with the wall for 0.1 s, then the force is
View SolutionA ball moving with a momentum of 5kgms−1 strikes against a wall at an angle of 45∘ and is reflected at the same angle calculate the change in momentum
View SolutionA body of mass m collides against a wall with the velocity v and rebounds with the same speed. Its magnitude of change of momentum is
View SolutionA 0.5kg ball moving with a speed of 12m/s strikes a hard wall at an angle of 30∘ with the wall. It is reflected with the same speed and at the same angle . If the ball is in contact with the wall for 0.25s, the average force acting on the wall is

View Solution
