when a constant power is delivered to an object, then the graph between velocity and position of the object is( motion of object is along x-axis)
_PHY_E05_253_Q01.png)
_PHY_E05_253_Q002.png)
_PHY_E05_253_Q03.png)
_PHY_E05_253_Q04.png)
To solve the problem of determining the graph between velocity and position of an object when a constant power is delivered to it, we can follow these steps:
Step 1: Understand the relationship between power, work, and kinetic energy
Power (P) is defined as the rate at which work is done. Mathematically, it is given by:
P=Wt
where W is the work done and t is the time.
Step 2: Relate work done to kinetic energy
According to the work-energy theorem, the work done on an object is equal to the change in its kinetic energy. For an object of mass m, the kinetic energy (KE) is given by:
KE=12mv2
Thus, we can express work done as:
W=P⋅t=12mv2
Step 3: Express velocity in terms of time
From the equation W=P⋅t, we can rearrange it to find the relationship between velocity and time. Since we have:
P⋅t=12mv2
Rearranging gives:
v2=2Ptm
This implies:
v∝t1/2
Step 4: Relate position to time
Since velocity v is the derivative of position x with respect to time t:
v=dxdt
Substituting the expression for v:
dxdt∝t1/2
This can be rewritten as:
dx∝t1/2dt
Step 5: Integrate to find position as a function of time
Integrating both sides:
∫dx=C∫t1/2dt
Where C is a constant. The integral of t1/2 is:
x=C⋅23t3/2+C1
Thus, we find:
x∝t3/2
Step 6: Establish the relationship between velocity and position
Since we have v∝t1/2 and x∝t3/2, we can express t in terms of x:
From x∝t3/2, we can write:
t∝x2/3
Substituting this back into the expression for v:
v∝(x2/3)1/2=x1/3
Step 7: Conclusion about the graph
Thus, we find that:
v∝x1/3
This means that the graph of velocity v versus position x is a curve that increases with x, specifically following the form v=kx1/3 for some constant k.
Final Answer
The graph between velocity and position of the object is a curve that represents v∝x1/3.
---
Power (P) is defined as the rate at which work is done. Mathematically, it is given by:
P=Wt
where W is the work done and t is the time.
According to the work-energy theorem, the work done on an object is equal to the change in its kinetic energy. For an object of mass m, the kinetic energy (KE) is given by:
KE=12mv2
Thus, we can express work done as:
W=P⋅t=12mv2
From the equation W=P⋅t, we can rearrange it to find the relationship between velocity and time. Since we have:
P⋅t=12mv2
Rearranging gives:
v2=2Ptm
This implies:
v∝t1/2
Since velocity v is the derivative of position x with respect to time t:
v=dxdt
Substituting the expression for v:
dxdt∝t1/2
This can be rewritten as:
dx∝t1/2dt
Integrating both sides:
∫dx=C∫t1/2dt
Where C is a constant. The integral of t1/2 is:
x=C⋅23t3/2+C1
Thus, we find:
x∝t3/2
Since we have v∝t1/2 and x∝t3/2, we can express t in terms of x:
From x∝t3/2, we can write:
t∝x2/3
Substituting this back into the expression for v:
v∝(x2/3)1/2=x1/3
Thus, we find that:
v∝x1/3
This means that the graph of velocity v versus position x is a curve that increases with x, specifically following the form v=kx1/3 for some constant k.
The graph between velocity and position of the object is a curve that represents v∝x1/3.
Similar Questions
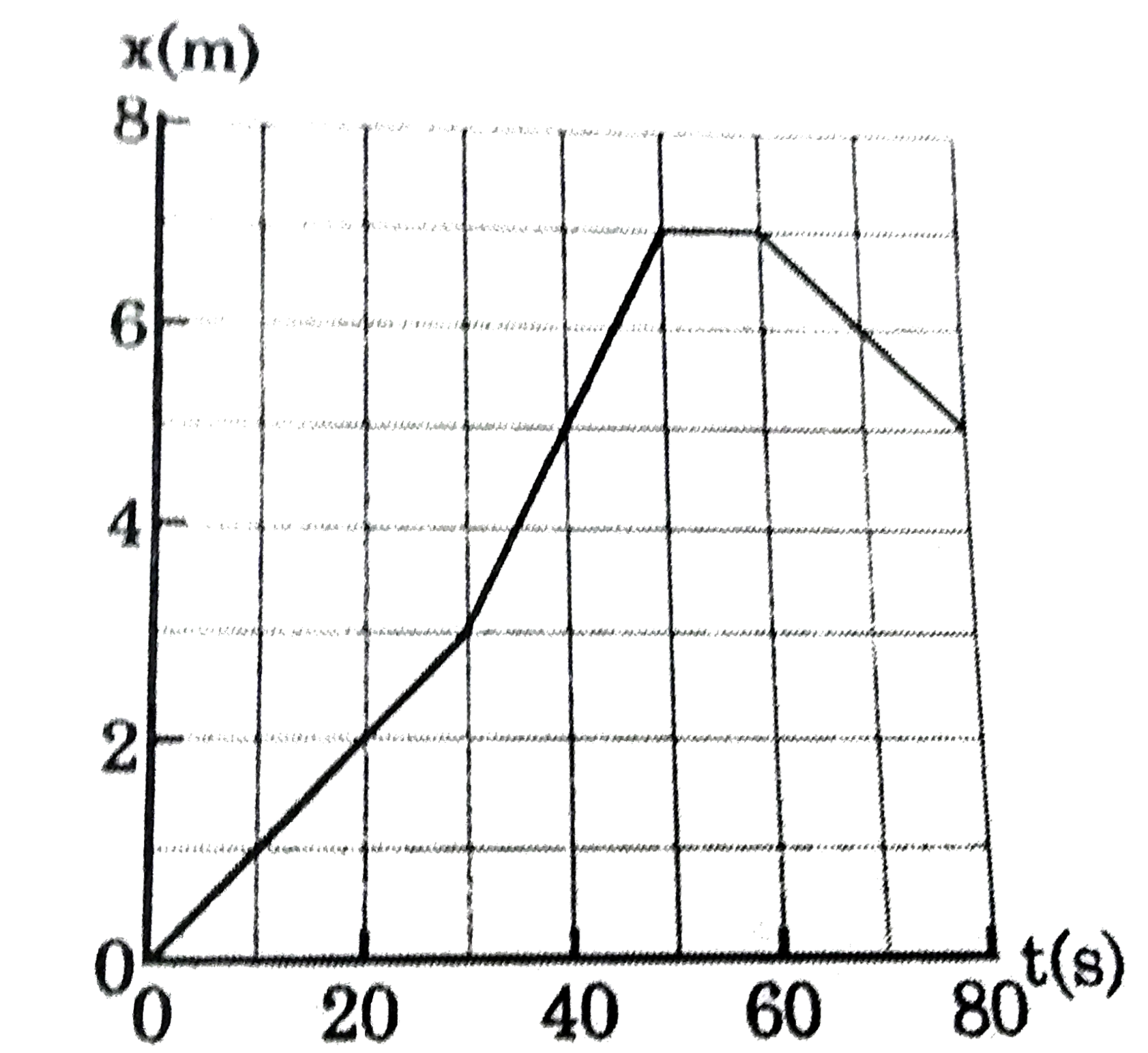
Graph represents motion of an object along X-axis for 80 s :-
View SolutionThe velocity-time graph of an object is shown below. The acceleration of the object is
View SolutionThe slope of velocity-time graph for uniform motion of an object is
View SolutionIn the given x - t graph. Find the position of an object at t = 3 second

View SolutionThe position-time graph of an object is given below. What is the velocity of the object?

View SolutionThe position-time graph of an object is given below. What is the velocity of the object?

View SolutionCan an object accelerate If its velocity is constant?
View SolutionFind the apparednt distance between the observer and the object shwon in the figure and shift in the position of object.

View SolutionHow will the equations of motion for an object moving with a uniform velocity change ?
View SolutionTerminal velocity (V) of a spherical object varies with a radius of object (r) -
View Solution
