A rod of uniform cross sectional area weighing and length is suspended vertically from a fixed support the elongation produced in the rod if [Young's modulus of material, and ]
To find the elongation produced in the rod, we can use the formula for Young's modulus (Y):
Y=StressStrain
Where:
- Stress = FA
- Strain = ΔLL
Here, F is the force acting on the rod, A is the cross-sectional area, ΔL is the elongation, and L is the original length of the rod.
Step 1: Calculate the Force (Weight) Acting on the Rod
The weight of the rod can be calculated using the formula:
F=mg
Given:
- Mass m=5kg
- Acceleration due to gravity g=10m/s2
Substituting the values:
F=5kg×10m/s2=50N
Step 2: Calculate the Cross-Sectional Area in m²
The area is given in mm², so we need to convert it to m²:
A=5mm2=5×10−6m2
Step 3: Calculate the Stress
Now we can calculate the stress using the formula:
Stress=FA
Substituting the values:
Stress=50N5×10−6m2=107N/m2
Step 4: Calculate the Strain
Using the Young's modulus formula, we can express strain as:
Strain=ΔLL
Rearranging gives us:
ΔL=Strain×L
Step 5: Calculate the Young's Modulus
We know:
Y=StressStrain
Rearranging gives us:
Strain=StressY
Substituting the values:
Strain=107N/m22×1011N/m2=5×10−5
Step 6: Calculate the Elongation (ΔL)
Now substituting the strain back into the elongation formula:
ΔL=Strain×L
Given L=1m:
ΔL=5×10−5×1m=5×10−5m=0.05mm
Final Answer
The elongation produced in the rod is:
ΔL=0.05mm
- Stress = FA
- Strain = ΔLL
The weight of the rod can be calculated using the formula:
- Mass m=5kg
- Acceleration due to gravity g=10m/s2
The area is given in mm², so we need to convert it to m²:
Now we can calculate the stress using the formula:
Using the Young's modulus formula, we can express strain as:
We know:
Now substituting the strain back into the elongation formula:
The elongation produced in the rod is:
Similar Questions
A uniform rod of length L and mass M is pulled horizontally on a smooth surface with a force F. Determine the elongation of rod if Young's modulus of the material is Y.
View SolutionA light rod of length L=2m is suspended horizontally from the ceiling by two wires A and B of equal lengths. The wire A is made of steel with the area of cross section AS=1×10−5m2, while the wire B is made of brass of cross sectional area Ab=2×10−5m2. A weight W is suspended at a distance x from the wire A as shown in figure.
Take, Young's modulus of steel and brass as Ys=2×1011Nm−2 and Yb=1×1011Nm−2.
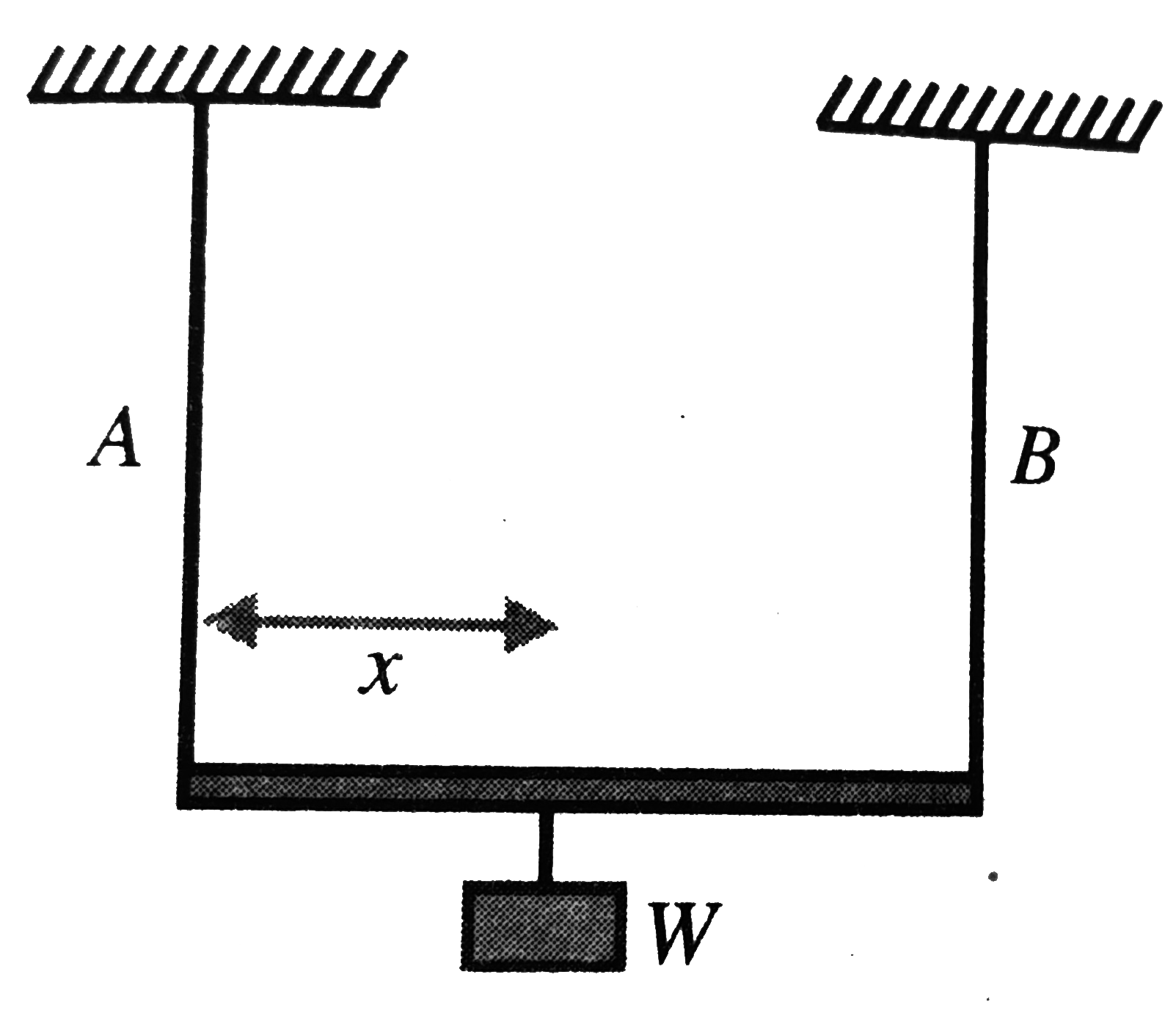
Determine the value of x so that equal strains are produced in each wire
View SolutionA light rod of length L=2m is suspended horizontally from the ceiling by two wires A and B of equal lengths. The wire A is made of steel with the area of cross section AS=1×10−5m2, while the wire B is made of brass of cross sectional area Ab=2×10−5m2. A weight W is suspended at a distance x from the wire A as shown in figure.
Take, Young's modulus of steel and brass as Ys=2×1011Nm−2 and Yb=1×1011Nm−2.
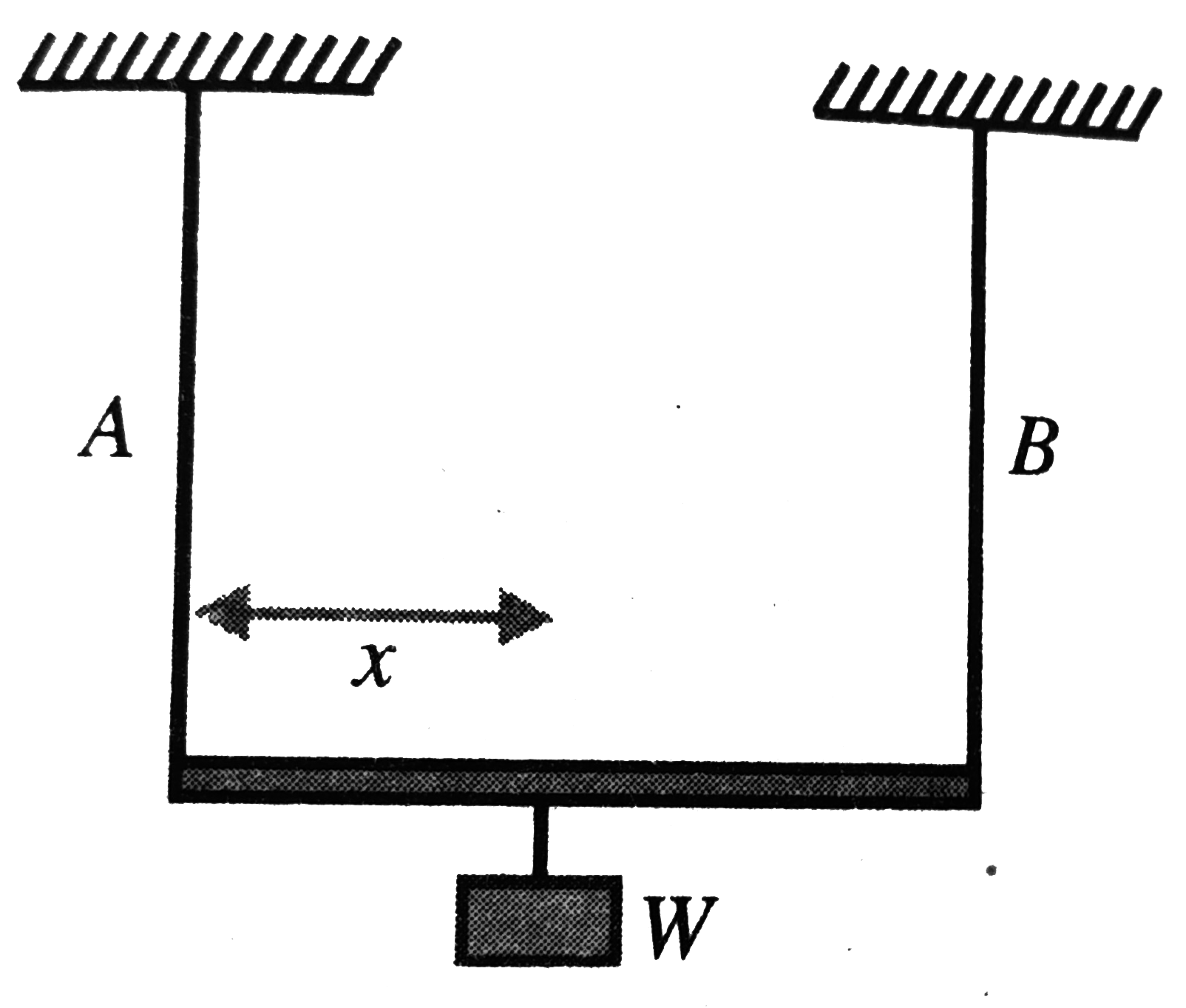
Determine the value of x so that equal stresses are produced in each wire.
View Solutionwire of length I has a ear mass density λ and area of cross-section A and the Young's modulus y is suspended vertically from rigid support. The extension produced in wire due to its own weight
View SolutionA stone of mass 1.3 kg is being rotated in a horizontal plane as a conical pendulum with the help of a 140 cm long aluminium wire of cross - sectional area 1mm2. The wire makes an angle θ=75∘ with the vertical. What is the increment in the length (in mm) of the wire? [Young's modulus of aluminium YAl=7×1010N m−2,
sin75∘≈0.97,cos75∘≈0.26,g=10ms−2]
View SolutionA brass rod of cross-sectional area 1cm2 and length 0.2 m is compressed lengthwise by a weight of 5 kg. if young's modulus of elasticity of brass is 1×1011N/m2 and g=10m/sec2 then increase in the energy of the rod will be
View SolutionA wire having a length 1 m and cross-section area 3mm2 is suspended at one of its ends from a ceiling. What will be its strain energy due to its own weight, if the density and Young's modulus of the material of the wire be 10g/cm3 and 1.2×1011N/m2 respectively.
View SolutionA light rod AC of length 2.00 m is suspended from the ceiling horizontally by means of two vertical wires of equal length tied to its ends. One of the wires is made of steel and is of cross-section 10−3m2 and the other is of brass of cross-section 2×10−3m2. The position of point D from end A along the rod at which a weight may be hung to produce equal stress in both the wires is [Young's modulus of steel is 2×1011Nm2 and for brass is 1×1011Nm−2]

View SolutionA steel rod of length l1=30cm and two identical brass rod of length l2=20cm each support a light horizontal platform as shown in Fig. Cross-sectional area of each of the three rods is A=1cm2. A vertically downward force F=5000N is applied on the platform. Young's modulus of elasticity for steel Ys=2×1011Nm−2 and brass Yb=1×1011Nm−2. Find stress (in MPa) developed in a. Steel rod b. Brass rod
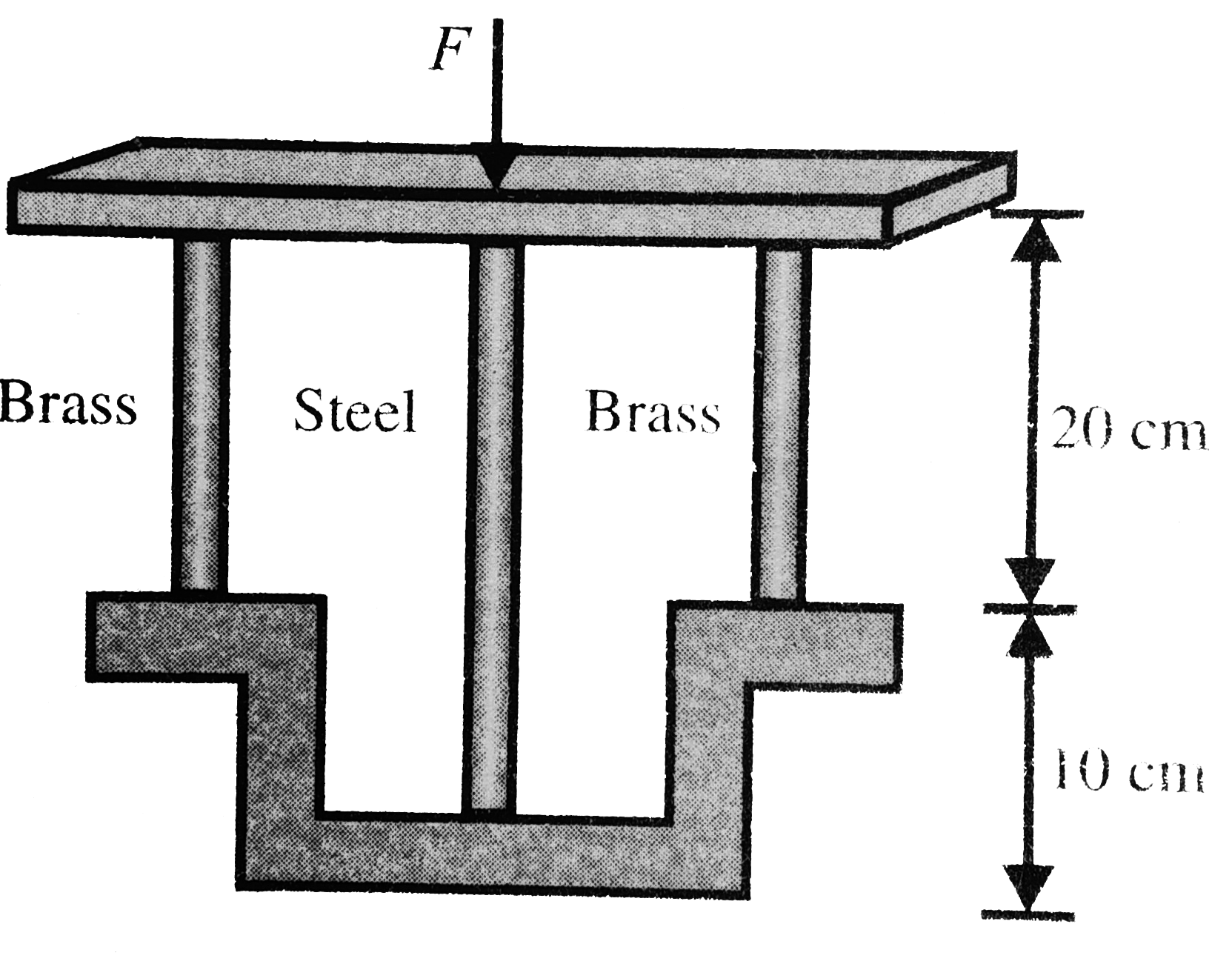
View SolutionOne end of a wire 2m long and 0.2 cm^2 in cross section is fixed in a ceiling and a load of 4.8 kg is attached to the free end. Find the extension of the wire. Young modulus of steel =2.0×1011Nm−2. Take g=10ms−2.
View Solution
