A brass rod of cross-sectional area 1cm2 and length 0.2 m is compressed lengthwise by a weight of 5 kg. if young's modulus of elasticity of brass is 1×1011N/m2 and g=10m/sec2 then increase in the energy of the rod will be
10−5joule
2.5×10−5 joule
5×10−5 joule
2.5×10−4 joule
The correct Answer is:B
To find the increase in energy of the brass rod when it is compressed, we can use the formula for elastic potential energy stored in the material due to deformation. The formula for the energy (U) stored in the rod is given by:
U=12FΔL
Where:
- F is the force applied,
- ΔL is the change in length of the rod.
Step 1: Calculate the Force (F)
The force applied on the rod can be calculated using the weight of the object compressing it. The weight (force due to gravity) is given by:
F=mg
Where:
- m=5kg (mass of the weight),
- g=10m/s2 (acceleration due to gravity).
Calculating the force:
F=5kg×10m/s2=50N
Step 2: Calculate the Change in Length (ΔL)
The change in length can be calculated using Young's modulus (Y), which is defined as:
Y=F/AΔL/L
Rearranging this gives us:
ΔL=F⋅LA⋅Y
Where:
- L=0.2m (original length of the rod),
- A=1cm2=1×10−4m2 (cross-sectional area),
- Y=1×1011N/m2 (Young's modulus of brass).
Substituting the values into the formula:
ΔL=50N×0.2m1×10−4m2×1×1011N/m2
Calculating ΔL:
ΔL=101×107=1×10−6m
Step 3: Calculate the Increase in Energy (U)
Now, we can substitute F and ΔL back into the energy formula:
U=12FΔL
Substituting the values:
U=12×50N×1×10−6m
Calculating U:
U=25×10−6J=2.5×10−5J
Thus, the increase in energy of the rod is:
2.5×10−5J
- F is the force applied,
- ΔL is the change in length of the rod.
The force applied on the rod can be calculated using the weight of the object compressing it. The weight (force due to gravity) is given by:
- m=5kg (mass of the weight),
- g=10m/s2 (acceleration due to gravity).
The change in length can be calculated using Young's modulus (Y), which is defined as:
- L=0.2m (original length of the rod),
- A=1cm2=1×10−4m2 (cross-sectional area),
- Y=1×1011N/m2 (Young's modulus of brass).
Now, we can substitute F and ΔL back into the energy formula:
Topper's Solved these Questions
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 1 (Surface Tension)
21 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 1 (Fluid Statics)
40 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)
3 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V B
19 Videos
- ERROR AND MEASUREMENTBOOK - ALLENCHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)
22 Videos
Similar Questions
The area of cross-section of a wire of length 1.1 meter is 1mm2. It is loaded with 1 kg. if young's modulus of copper is 1.1×1011N/m2 then the increase in length will be (if g=10m/s2)-
View SolutionWhat is the percentage increase in length of a wire of diameter 2.5 mm, stretched by a force of 100 kg wt ? Young's modulus of elasticity of wire =12.5×1011dyne/cm2.
View SolutionYoung 's modulus of steel is 2.0×1011Nm/(2). Express it is dynecm2.
View SolutionA uniform wire of length 6m and a cross-sectional area 1.2 cm2 is stretched by a force of 600N . If the Young's modulus of the material of the wire 20×1010Nm−2 , calculate (i) stress (ii) strain and (iii) increase in length of the wire.
View SolutionThe length of a rod is 20cm and area of cross-section 2cm2. The Young's modulus of the material of wire is 1.4×1011N/m2. If the rod is compressed by 5kg−wt along its length, then increase in the energy of the rod in joules will be
View SolutionA light rod of length L=2m is suspended horizontally from the ceiling by two wires A and B of equal lengths. The wire A is made of steel with the area of cross section AS=1×10−5m2, while the wire B is made of brass of cross sectional area Ab=2×10−5m2. A weight W is suspended at a distance x from the wire A as shown in figure.
Take, Young's modulus of steel and brass as Ys=2×1011Nm−2 and Yb=1×1011Nm−2.
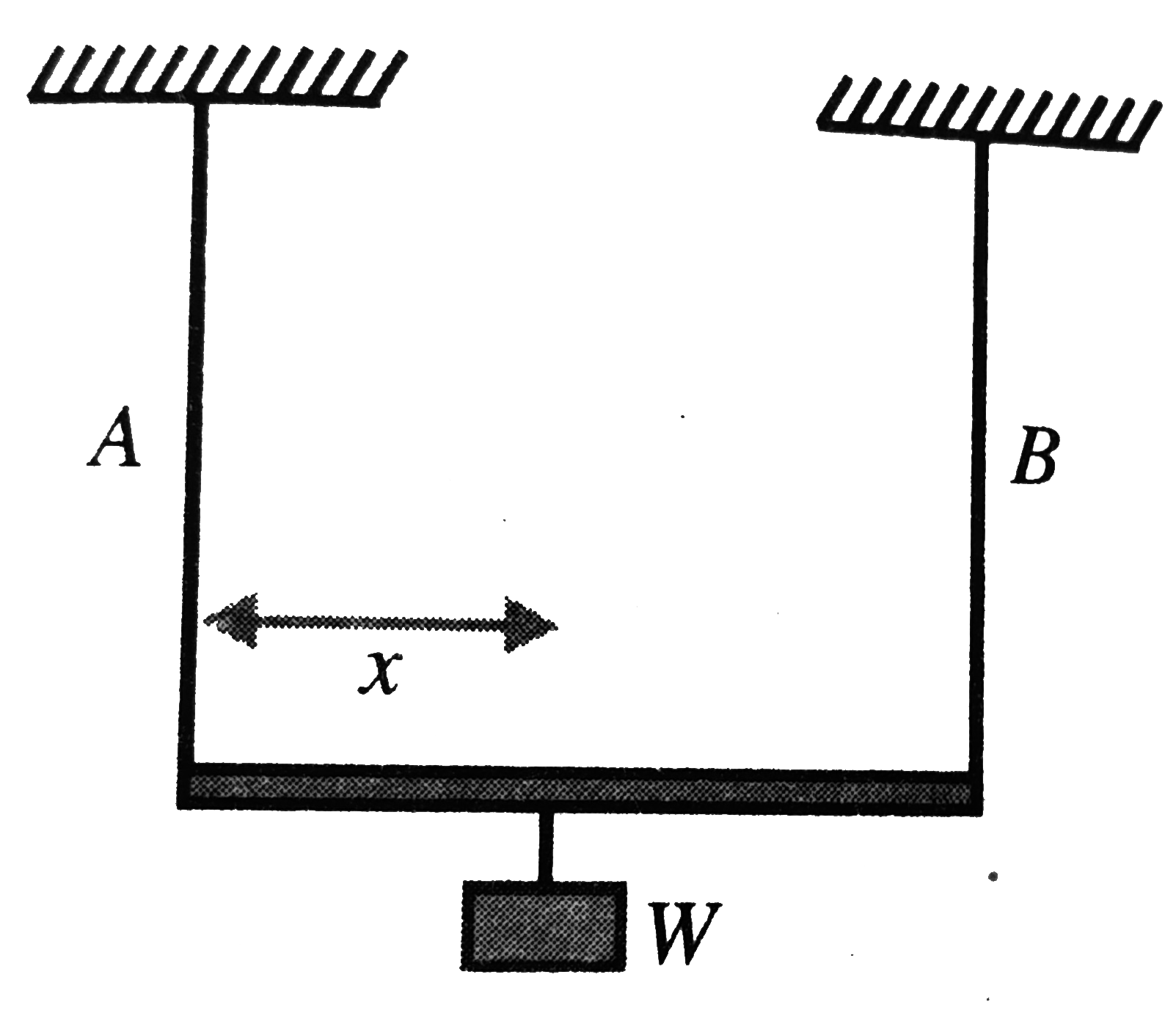
Determine the value of x so that equal strains are produced in each wire
View SolutionA light rod of length L=2m is suspended horizontally from the ceiling by two wires A and B of equal lengths. The wire A is made of steel with the area of cross section AS=1×10−5m2, while the wire B is made of brass of cross sectional area Ab=2×10−5m2. A weight W is suspended at a distance x from the wire A as shown in figure.
Take, Young's modulus of steel and brass as Ys=2×1011Nm−2 and Yb=1×1011Nm−2.
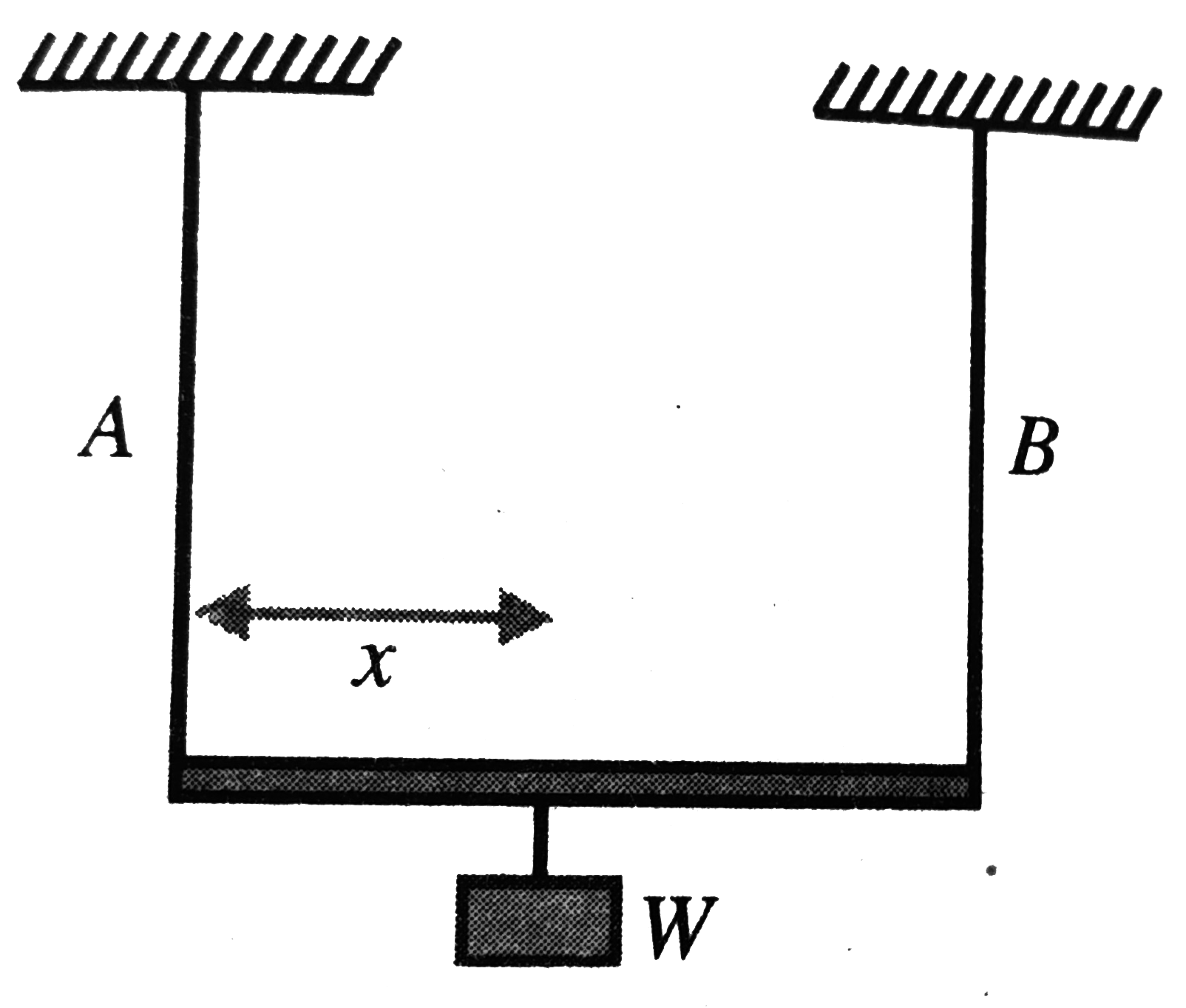
Determine the value of x so that equal stresses are produced in each wire.
View SolutionA uniform bar of length 2 m and cross-sectional area 50cm2 is subjected to a tensile load 100 N. If Young's modulus of material of bar is 2×107N/m2 and poisson's ratio is 0.4, then determine the volumetric strain.
View SolutionA rod of uniform cross sectional area 5mm2 weighing5kg and length 1m is suspended vertically from a fixed support the elongation produced in the rod if [Young's modulus of material, Y=2x1011Nm2 and g=10ms−2]
View SolutionA structural steel rod has a radius r =10mm and a length l.=1m When a force F=100kN is applied, it stretches it along its length. Young's modulus of elasticity of the structural steel is 2.0×1011Nm−2. What is the elastic energy density of the steel rod ?
View Solution
