If two resistive wires AB and CD are made to slide on the conducting rails with speeds 5m/s 10 m/s respectively towards right as shown in the figure then value of R for which current through it is 1A is( B=1.5T)
283Ω
133Ω
7Ω
2Ω
To solve the problem step by step, we need to find the resistance R for which the current through the circuit is 1 A, given the speeds of the wires and the magnetic field strength.
Step 1: Calculate the EMF induced in each wire
The induced EMF E in a wire moving in a magnetic field can be calculated using the formula:
E=B⋅v⋅l
where:
- B is the magnetic field strength (1.5 T),
- v is the speed of the wire,
- l is the length of the wire (1 m).
For wire AB (moving at 5 m/s):
E1=1.5T⋅5m/s⋅1m=7.5V
For wire CD (moving at 10 m/s):
E2=1.5T⋅10m/s⋅1m=15V
Step 2: Calculate the equivalent resistance of the circuit
The two wires have resistances R1=1Ω and R2=2Ω. The equivalent resistance Reff of the two resistors in parallel is given by:
1Reff=1R1+1R2
Substituting the values:
1Reff=11+12=1+0.5=1.5
Thus,
Reff=11.5=23Ω
Step 3: Calculate the total EMF in the circuit
The total EMF Etotal in the circuit is the sum of the individual EMFs:
Etotal=E1+E2=7.5V+15V=22.5V
Step 4: Use Ohm's Law to find the total resistance
According to Ohm's Law:
I=EtotalReff+R
Given that the current I is 1 A, we can set up the equation:
1=22.523+R
Step 5: Solve for R
Rearranging the equation gives:
23+R=22.5
Subtracting 23 from both sides:
R=22.5−23
Converting 22.5 to a fraction:
22.5=67.53
Thus,
R=67.53−23=67.5−23=65.53=196.59
This simplifies to:
R=283Ω
Final Answer
The value of R for which the current through it is 1 A is:
R=283Ω
The induced EMF E in a wire moving in a magnetic field can be calculated using the formula:
E=B⋅v⋅l
where:
- B is the magnetic field strength (1.5 T),
- v is the speed of the wire,
- l is the length of the wire (1 m).
E1=1.5T⋅5m/s⋅1m=7.5V
E2=1.5T⋅10m/s⋅1m=15V
The two wires have resistances R1=1Ω and R2=2Ω. The equivalent resistance Reff of the two resistors in parallel is given by:
1Reff=1R1+1R2
Substituting the values:
1Reff=11+12=1+0.5=1.5
Thus,
Reff=11.5=23Ω
The total EMF Etotal in the circuit is the sum of the individual EMFs:
Etotal=E1+E2=7.5V+15V=22.5V
According to Ohm's Law:
I=EtotalReff+R
Given that the current I is 1 A, we can set up the equation:
1=22.523+R
Rearranging the equation gives:
23+R=22.5
Subtracting 23 from both sides:
R=22.5−23
Converting 22.5 to a fraction:
22.5=67.53
Thus,
R=67.53−23=67.5−23=65.53=196.59
This simplifies to:
R=283Ω
The value of R for which the current through it is 1 A is:
R=283Ω
Similar Questions
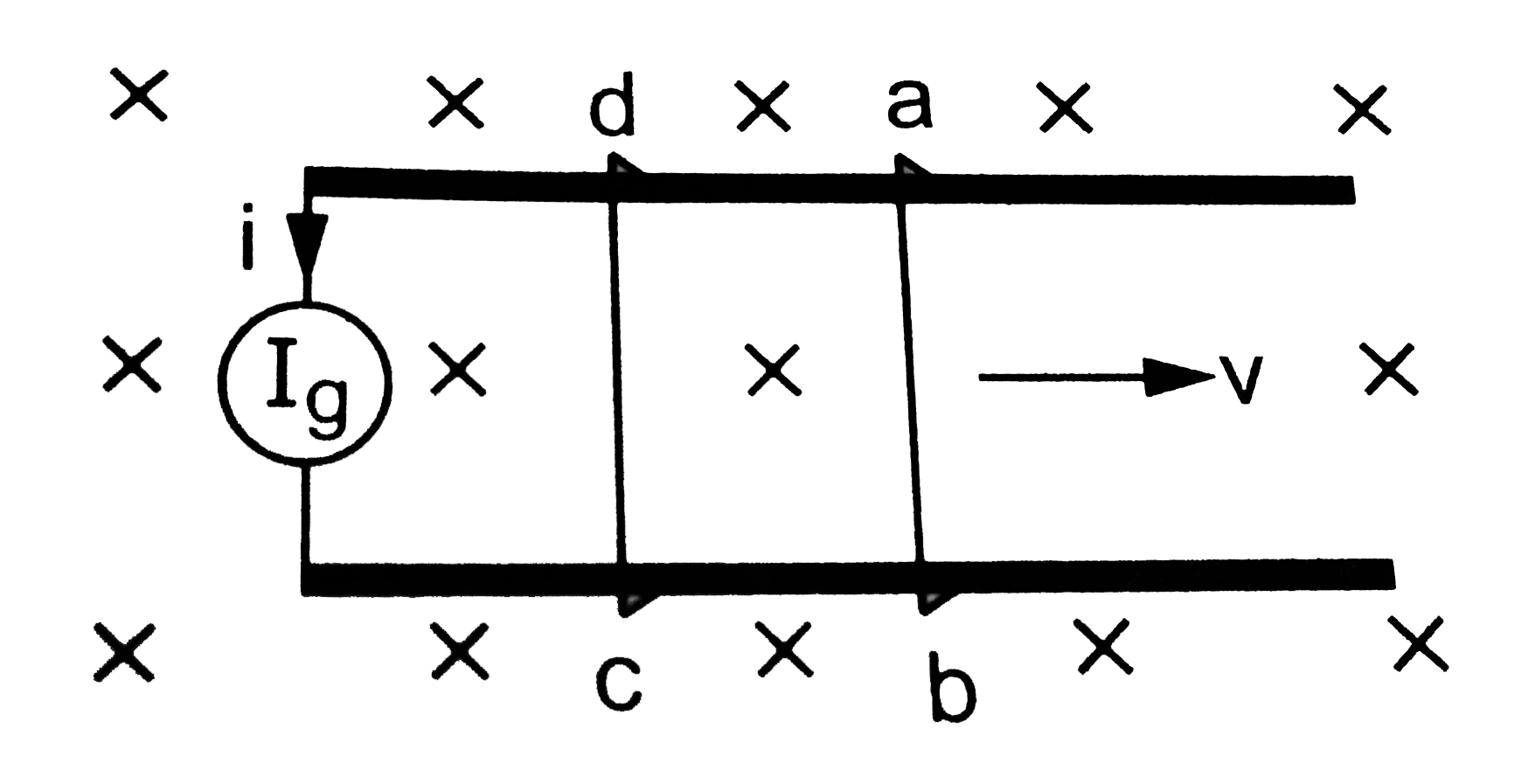
The current generator Ig, shown in . Sends a constant current I throught the curcuti. The wire cd is fixed and ab is made ot slide on the smooth, thick rails with a constant velocity v towards right. Each of these wire has resistance r. Find the current through the wire cd.
View SolutionChoose the correct option:
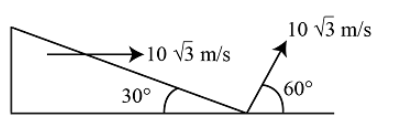
A particle is projected at an angle 60∘ with speed 10(√3)m/s, from the point A, as shown in the figure. At the same time the wedge is made to move with speed 10(√3)m/s towards right as shown in the figure. Then the time after which particle will strike with wedge is
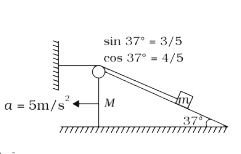
View SolutionAs shown in the figure, if acceleration of M with respect to ground is 5m/s2, then :
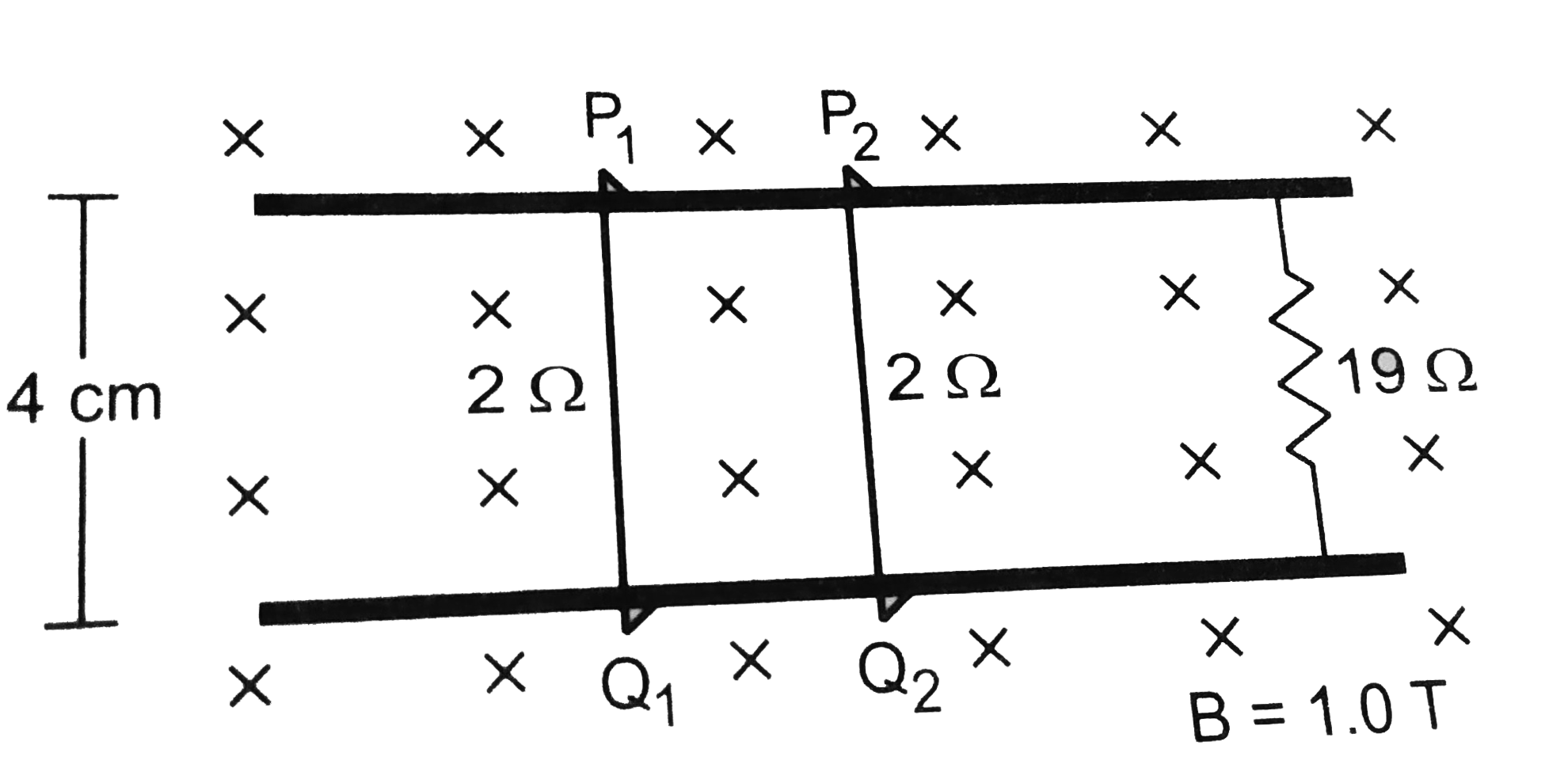
View SolutionIn the figure shown , the wires P1Q1 and P2Q2 are made to slide on the rails with same speed of 5cms−1. In this region a magnetic field of 1T exists. The electric current in the 9Ω resistance is :

View SolutionIn the diagram shown, the wires P1Q1 and P2Q2 each of length 40cm are made to slide on the rails with same speed of 5m/s. In this region a magnetic field of 1T exists. The electric current in 9kΩ resistor is

View SolutionConsider the situation shown in figure. The wires P1Q1 and P2Q2 are made to slide on the rails with the same speed 5cm/sec . Find the electric current in the 19Ω resistor if (a) both the wires move towards right and (b) if P 1Q1 moves towards left but P2Q2 moves towards right.
View SolutionConsider the situation shown in . The wires P1Q1 and P2Q2 are made to slide on the rails with the same speed 5cms−1. Find the electric current in the 19Ω resistorif (a) both the wires move towards right and (b) if P1Q1 moves towards left but P2Q2 moves towards right.
View SolutionTwo particles A and B of mass 3kg and 2kg moving with speed 10m/s and 5m/s as shown in figure.
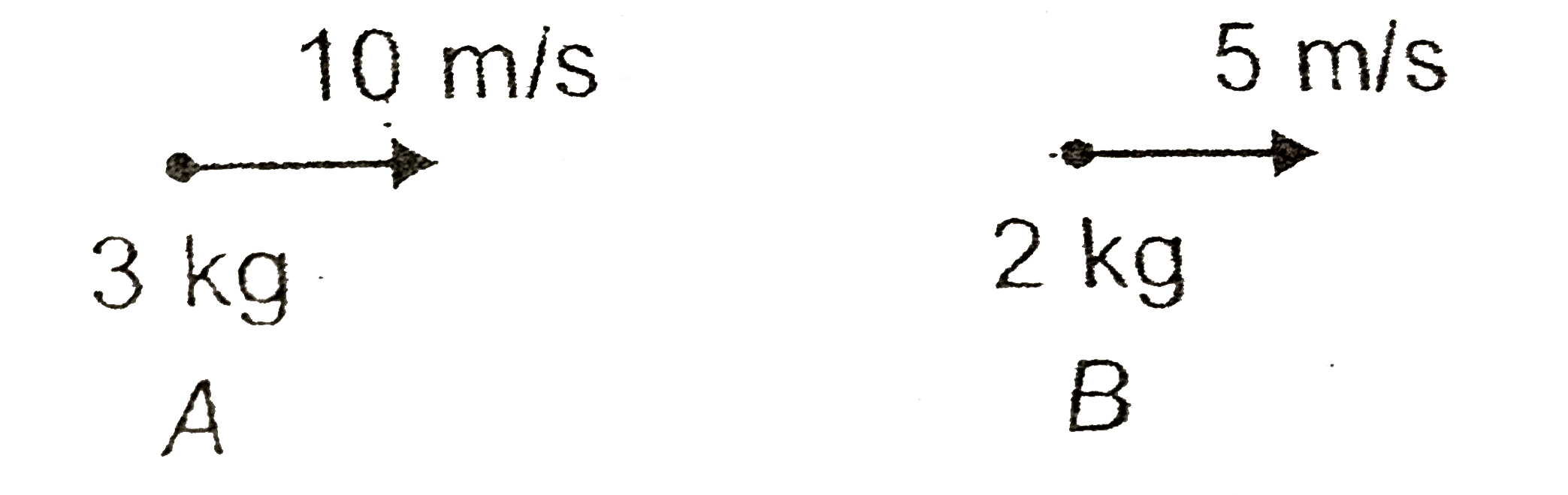
Kinetic energy of particle A when particle B has the maximum momentum
View SolutionConsider the situation shown in . The wire PQ has a negligible resistance and is made to slide on the three rails with a constant speed of 5cms−1 . Find the current in the 10Ω resistor when the switch S is thrown to (a) the middle rail (b) the bottom rail.

View SolutionConsider the situation shown in . The wire PQ has a negligible resistance and is made to slide on the three rails with a constant speed of 5cms−1 . Find the current in the 10Ω resistor when the switch S is thrown to (a) the middle rail (b) the bottom rail.

View Solution
