A metallic rod of mass m and resistance R is sliding over the 2 conducting frictionless rails as shown in Fig. An infinitely long wire carries a current I0. The distance of the rails from the wire are b and a respectively.
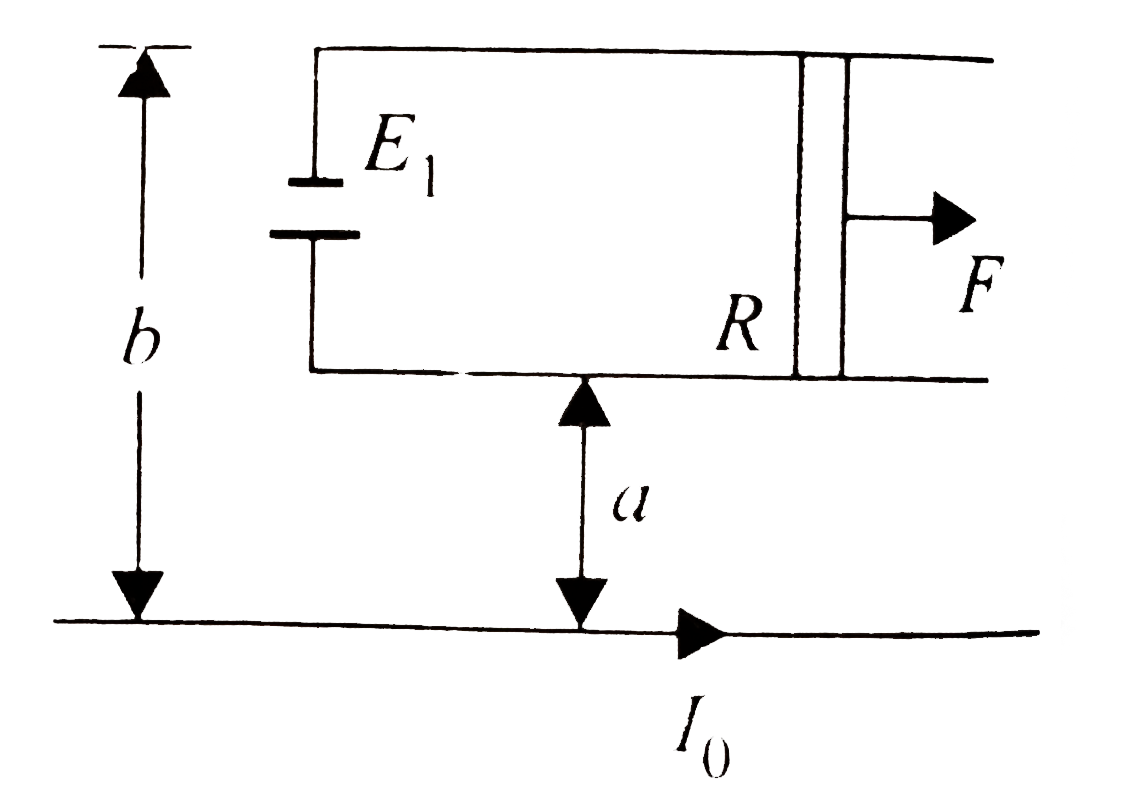
Find the value of current in the circuit if the rod slides with constant velocity v0
1R{E−μ0I0v02π1n∣∣∣ba∣∣∣}
1R{E+μ0I0v02π1n∣∣∣ba∣∣∣}
1R{E−μ0I0v0π1n∣∣∣ba∣∣∣}
None of these
The correct Answer is:A
Step by step video, text & image solution for A metallic rod of mass m and resistance R is sliding over the 2 conducting frictionless rails as shown in Fig. An infinitely long wire carries a current I_(0). The distance of the rails from the wire are b and a respectively. Find the value of current in the circuit if the rod slides with constant velocity v_(0) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Integer
12 Videos
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Multiple Correct
34 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False
3 Videos
- Moving charges and magnetismBOOK - CENGAGE PHYSICSCHAPTER - Moving charges and magnetismEXERCISE - Question Bank
20 Videos
Similar Questions
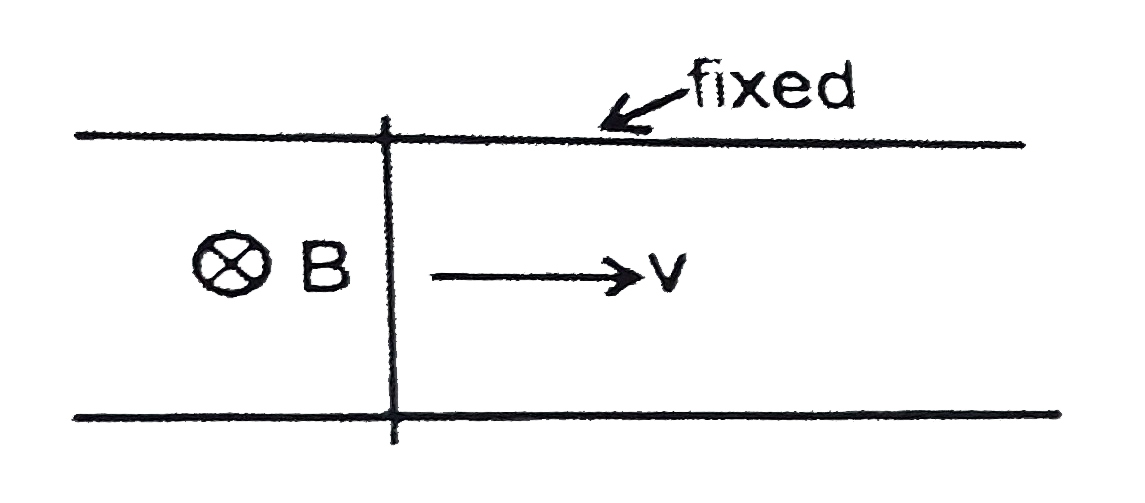
Figure shows a wire of resistance R sliding on two parallel, conducting fixed thick rails placed at a separation l. A magnetic fild B exist in a direction perpendicular to the plane of the rails. The wire is moving with a constant velocity v. Find current through the wire
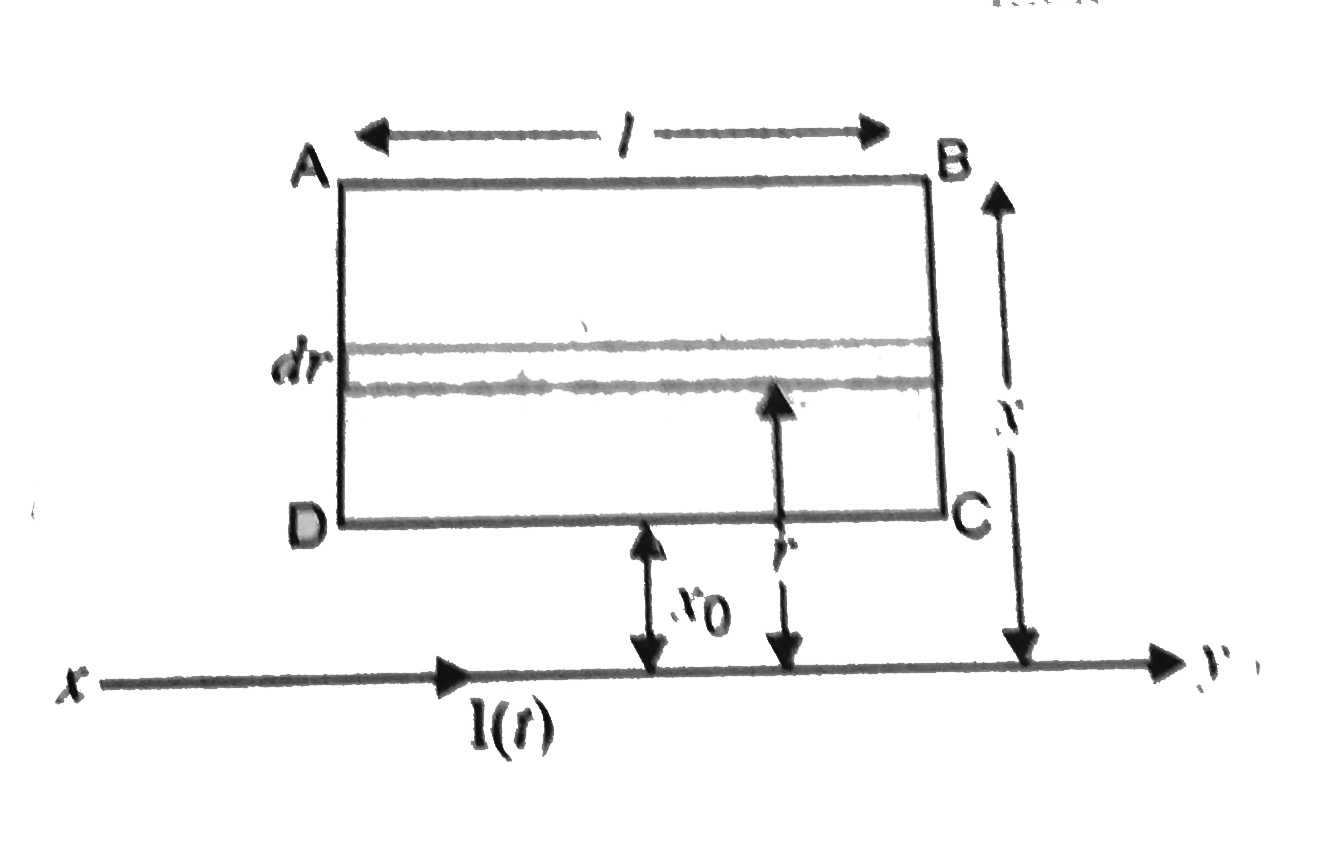
View SolutionConsider an infinitely long wire carrying a current I (t),
With dIdt=λ = constant . Find the current produced in the rectangular loop of wire ABCD if its resistance is R, Fig
View Solution
Knowledge Check
A metallic rod of mass m and resistance R is sliding over the 2 conducting frictionless rails as shown in Fig. An infinitely long wire carries a current I0. The distance of the rails from the wire are b and a respectively.
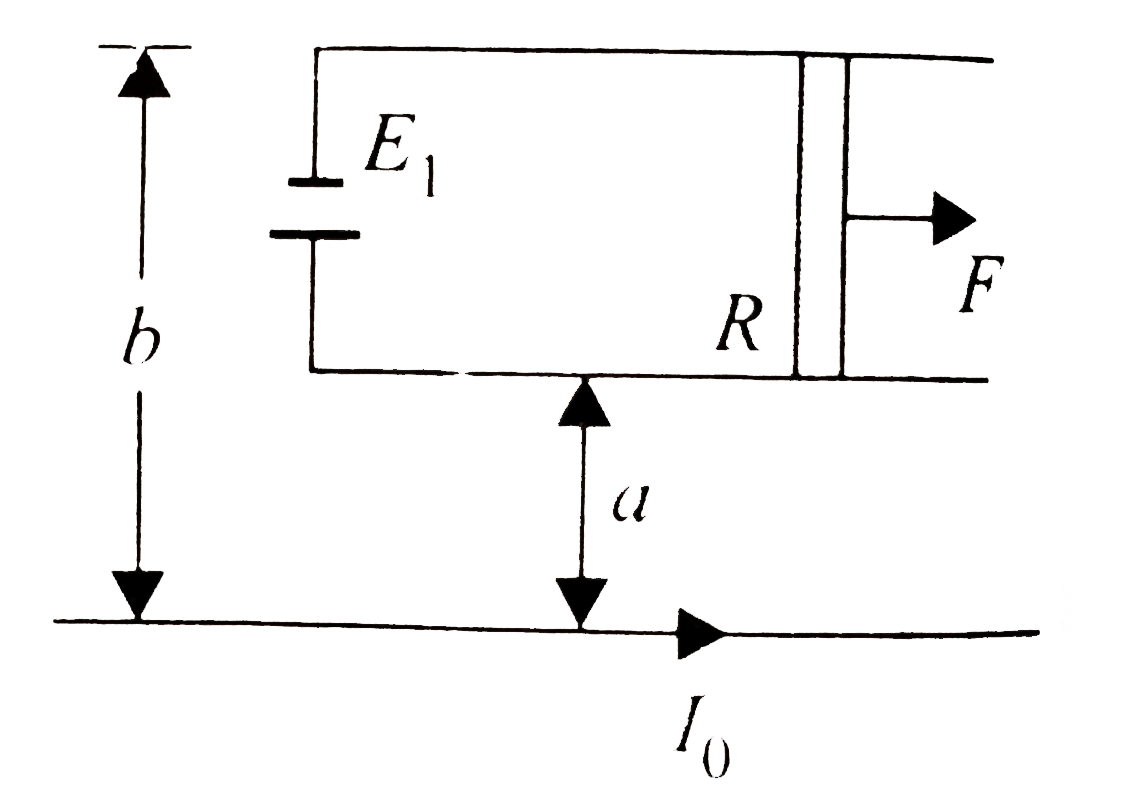
Find the value of F if the rod slides with constant velocityAμ0I02πR[E+μ0I02πv01n∣∣∣ba∣∣∣]1n(ba)Bμ0I0πR[E−μ0I02πv01n∣∣∣ba∣∣∣]1n(ba)Cμ0I02πR[E−μ0I02πv01n∣∣∣ba∣∣∣]1n(ba)DNone of theseThe magnetic induction due to an infinitely long straight wire carrying a current i at a distance r from wire is given by
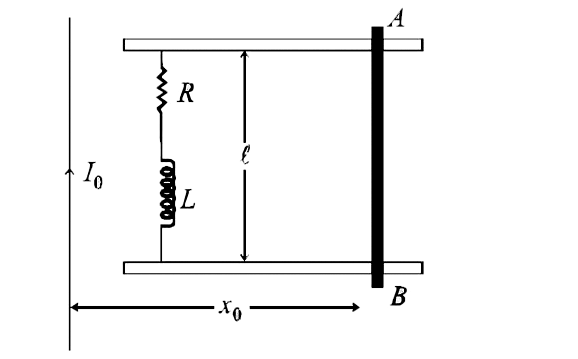
A|B|=(μ04π)2irB|B|=(μ04π)r2iC|B|=(4πμ0)2irD|B|=(4πμ0)r2iA metal bar AB can slide without friction on two parallel thick metallic rails separated by a distance I. A resistance R and an inductance L are connected to the rails as shown in the figure. An infinite long straight wire carrying a constant current I0 is placed on the plane of the rails as shown. The bar AB is held at rest at a distance x0 from the long wire. At t = 0, it is made to slide on the rails away from the wire.
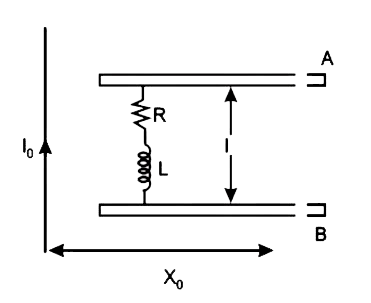
It is observed that at time t = T, the metal bar AB is at a distance of 2x0 from the long wire and the resistance R carries a current ix. Obtain an expression for the net charge that has flown through resistance R from t = 0 to t = T.A1R[μ0I2πln(2)−Li1]B1R[l2πI0ln(2)−Li1]C1R[μ0I0l2πln(2)−Li1]D1R[μ0I02πln(2)−Li1]
A metal bar AB can slide on two parallel thick metallic rails separated by a distance l. A resistance R and an inductance L are connected to the rails as shown in the figure. A long straight wire carrying a constant current I0 is placed in the plane of the rails and perpendicular to them as shown. The bar AB is held at rest at a distance x0 from the long wire. At t=0, it is made to slide on the rails away from wire. Answer the following questions.
(a) Find a relation among i,didtanddϕdt, where i is the current in the circuit and ϕ is the flux of the megnetic field due to the long wire through the circuit.
(b) It is observed that at time t=T, the metal bar AB si at a distance of 2x0 from the long wire and the resistance R carries a current (i1). Obtain an expression for the net charge that has flown through riesistance R form t=0 to t=T.
(c) THe bar is suddenly stopped at time T. THe current through resistance R is found to be i14 at time 2T. Find the value of LR in terms of hte other given quantities.
View SolutionA rod of length l is placed perpendicular to a long wire carrying current i. The rod is moved parallel to the wire with a velocity v. Find the emf induced in the rod, if its nearest end is at a distance a from the wire.
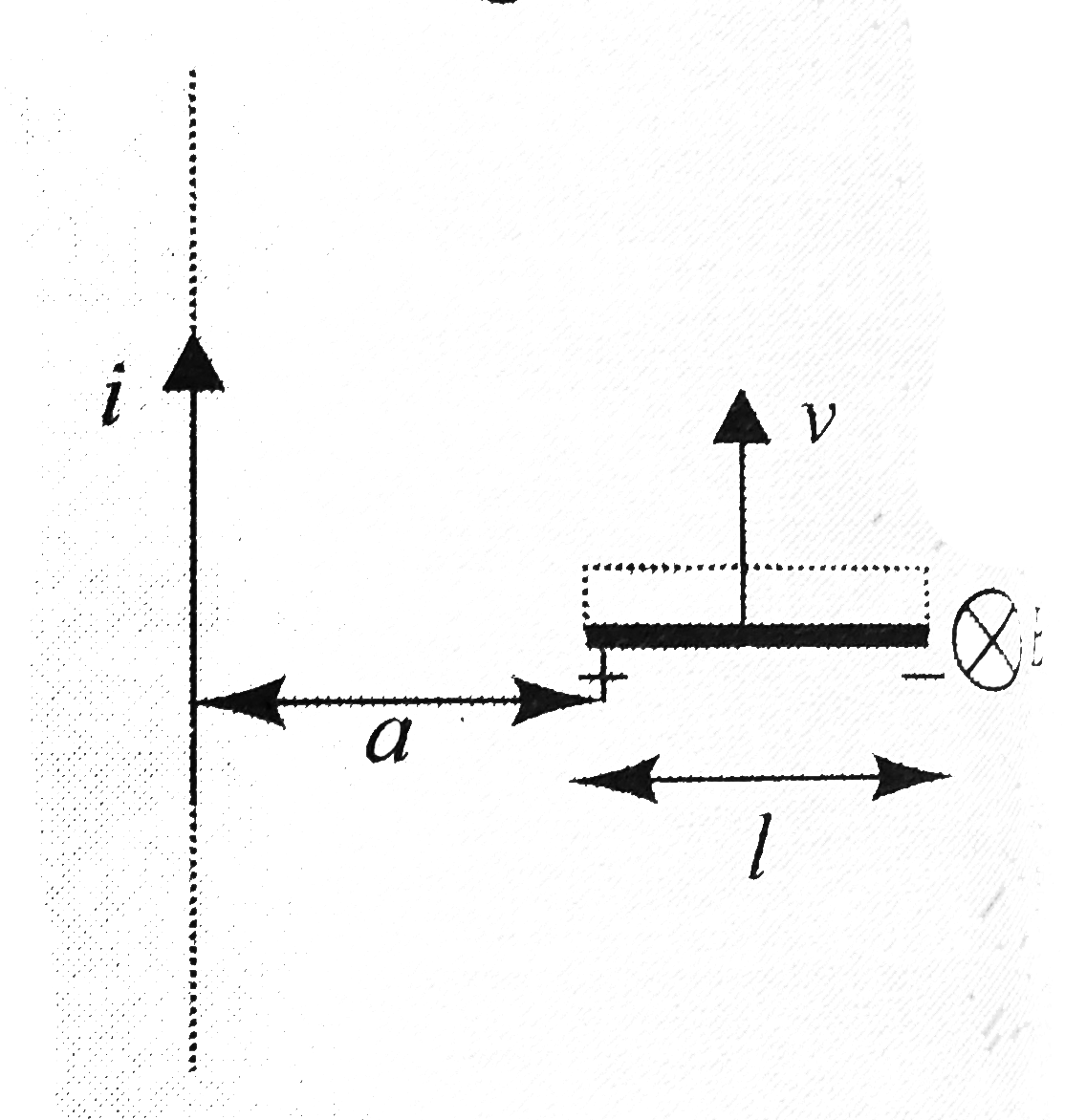
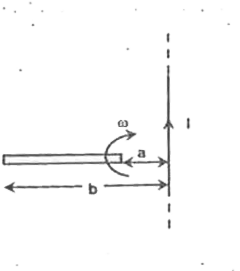
View SolutionA copper rod moves with a constant angular velocity ω about a long straight wire carrying a current I. If the ends of the rod from the wire are at distances a and b, then the e.m.f induced in the rod is
View SolutionIn the figure shown AB is a plastic rod moving with a constant velocity v, W is an infinite long wire carrying current I. The end of the rod which is at higher potential is

View SolutionA conducting rod of mass m and length l is free to move without friction on two parallel long conducting rails, as shown below. There is a resistance R across the rails. In the entire space around, there is a uniform magnetic field B normal to the plane of the rod and rails. The rod is given an impulsive velocity v0-

Finally, the initial energy 12mv20
View Solution
