A conducting rod AB of length l is rotated about point O with an angular velocity velocity omega in a uniform magnetic field (B_0) directed perpendicular into the plane of rotation as shown in the figure. The value of VB−VA is
−(16)B0l2ω
(16)B0l2ω
(118)B0l2ω
−(118)B0l2ω
To solve the problem of finding the potential difference VB−VA for a conducting rod AB of length l rotating in a magnetic field, we can follow these steps:
1. Understand the Setup:
The conducting rod AB of length l is rotating about point O with an angular velocity ω in a uniform magnetic field B0 directed perpendicular to the plane of rotation.
2. Identify the Points:
Let point A be at a distance 0 from point O and point B be at a distance l from point O. The rod can be divided into segments for integration.
3. Expression for EMF:
The electromotive force (EMF) induced in the rod can be calculated using the formula:
V=∫B⋅v⋅dx
where v is the linear velocity at a distance x from point O, given by v=ωx.
4. Calculate VB:
For point B, we need to integrate from 0 to l3 (assuming the rod is divided into segments):
VB=∫l30B0⋅(ωx)dx
VB=B0ω∫l30xdx
VB=B0ω(x22)l30=B0ω⋅12⋅(l3)2=B0ωl218
5. Calculate VA:
For point A, we integrate from 0 to 2l3:
VA=∫2l30B0⋅(ωx)dx
VA=B0ω∫2l30xdx
VA=B0ω(x22)2l30=B0ω⋅12⋅(2l3)2=B0ω⋅2l29
6. Find VB−VA:
Now, we can find the potential difference:
VB−VA=B0ωl218−B0ω⋅2l29
To combine these, we can express 2l29 in terms of 1818:
VB−VA=B0ωl218−4B0ωl218=−3B0ωl218=−B0ωl26
7. Final Result:
The value of VB−VA is:
VB−VA=B0ωl218
The conducting rod AB of length l is rotating about point O with an angular velocity ω in a uniform magnetic field B0 directed perpendicular to the plane of rotation.
Let point A be at a distance 0 from point O and point B be at a distance l from point O. The rod can be divided into segments for integration.
The electromotive force (EMF) induced in the rod can be calculated using the formula:
V=∫B⋅v⋅dx
where v is the linear velocity at a distance x from point O, given by v=ωx.
For point B, we need to integrate from 0 to l3 (assuming the rod is divided into segments):
VB=∫l30B0⋅(ωx)dx
VB=B0ω∫l30xdx
VB=B0ω(x22)l30=B0ω⋅12⋅(l3)2=B0ωl218
For point A, we integrate from 0 to 2l3:
VA=∫2l30B0⋅(ωx)dx
VA=B0ω∫2l30xdx
VA=B0ω(x22)2l30=B0ω⋅12⋅(2l3)2=B0ω⋅2l29
Now, we can find the potential difference:
VB−VA=B0ωl218−B0ω⋅2l29
To combine these, we can express 2l29 in terms of 1818:
VB−VA=B0ωl218−4B0ωl218=−3B0ωl218=−B0ωl26
The value of VB−VA is:
VB−VA=B0ωl218
Similar Questions
A conducting rod OA of length l is rotated about its end O with an angular velocity ω in a uniform magnetic field directed perpendicualr to the rotation. Find the emf induced in the rod, between it's ends.
View SolutionA conducting loop rotates with constant angular velocity about its fixed diameter in a uniform magnetic field, whose direction is perpendicular to that fixed diameter.
View SolutionA conducting loop rotates with constant angular velocity about its fixed diameter in a uniform magnetic field, whose direction is perpendicular to that fixed diameter.
View SolutionA conducting rod AB of length l=1m is moving at a velocity vA=4m/s making an angle 30∘ with its length. A uniform magnetic field B=2T exists in a direction perpendicular to the plane of motion. Then
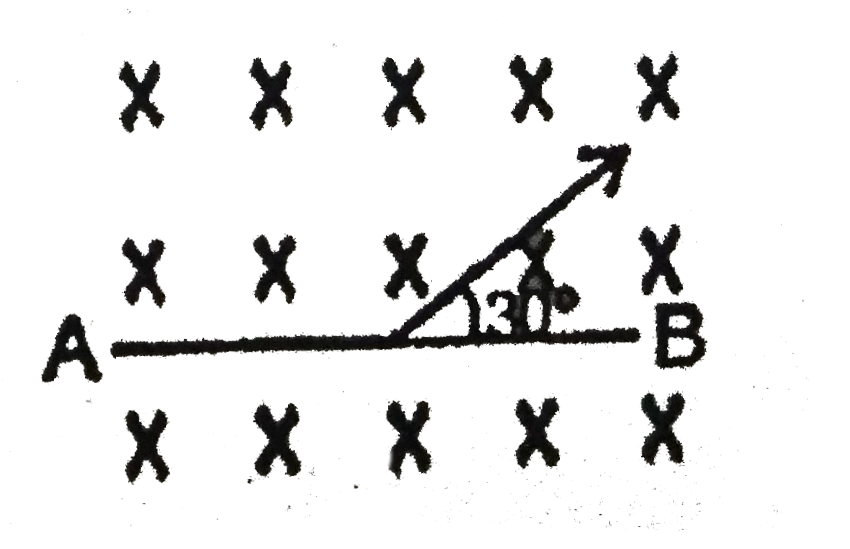
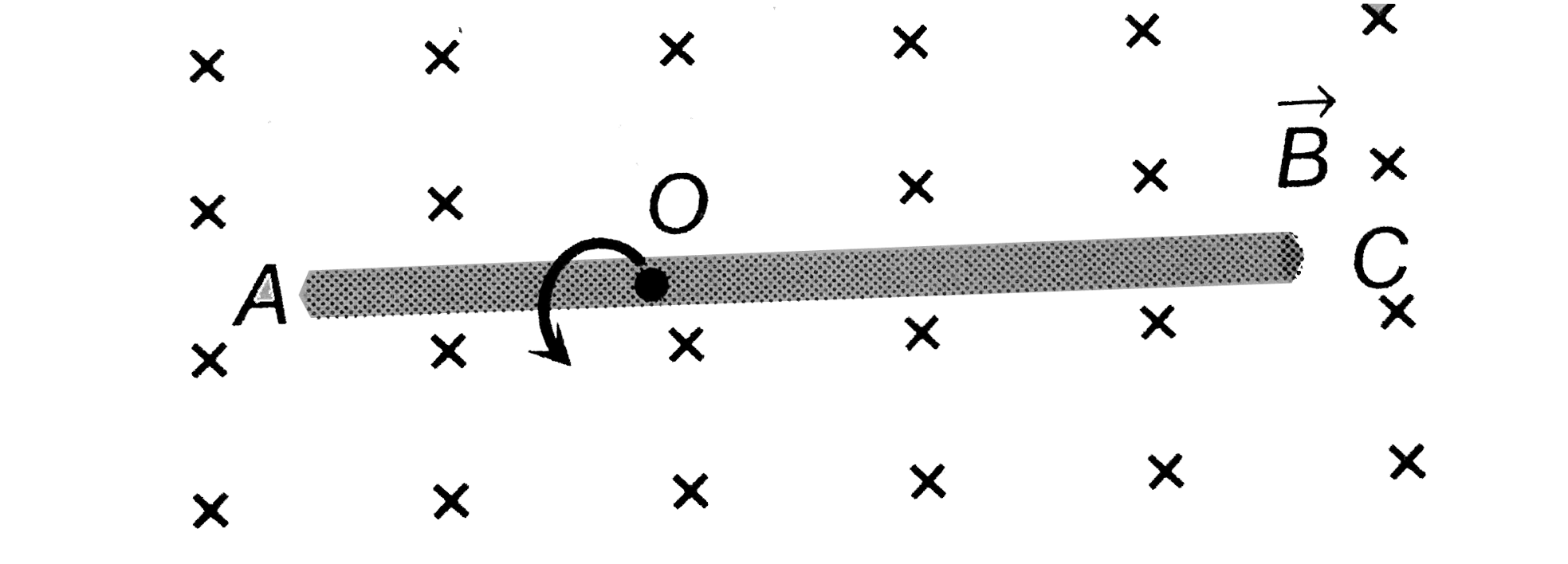
View SolutionA conducting rod AC of length 4l is rotated about point O in a uniform magnetic field →B directed into the plane of the paper. AO=landOC=3l. Find VA−VC.

View SolutionA conducting circular loop of radius r is rotated about its diameter at a constant angular velocity ω in a magnetic field B perpendicular to the axis of rotation. In what position of the loop is the induced emf zero?
View SolutionA conducting rod AC of length 4l is rotate about a point O in a uniform magnetic field →B directed into the paper. AO=l and OC=3l. Then
View SolutionA wooden stick of length 3l is rotated about an end with constant angular velocity ω in a uniform magnetic field B perpendicular to the plane of motion. If the upper one-third of its length is coated with copper, the potential difference across the whole length of the stick is
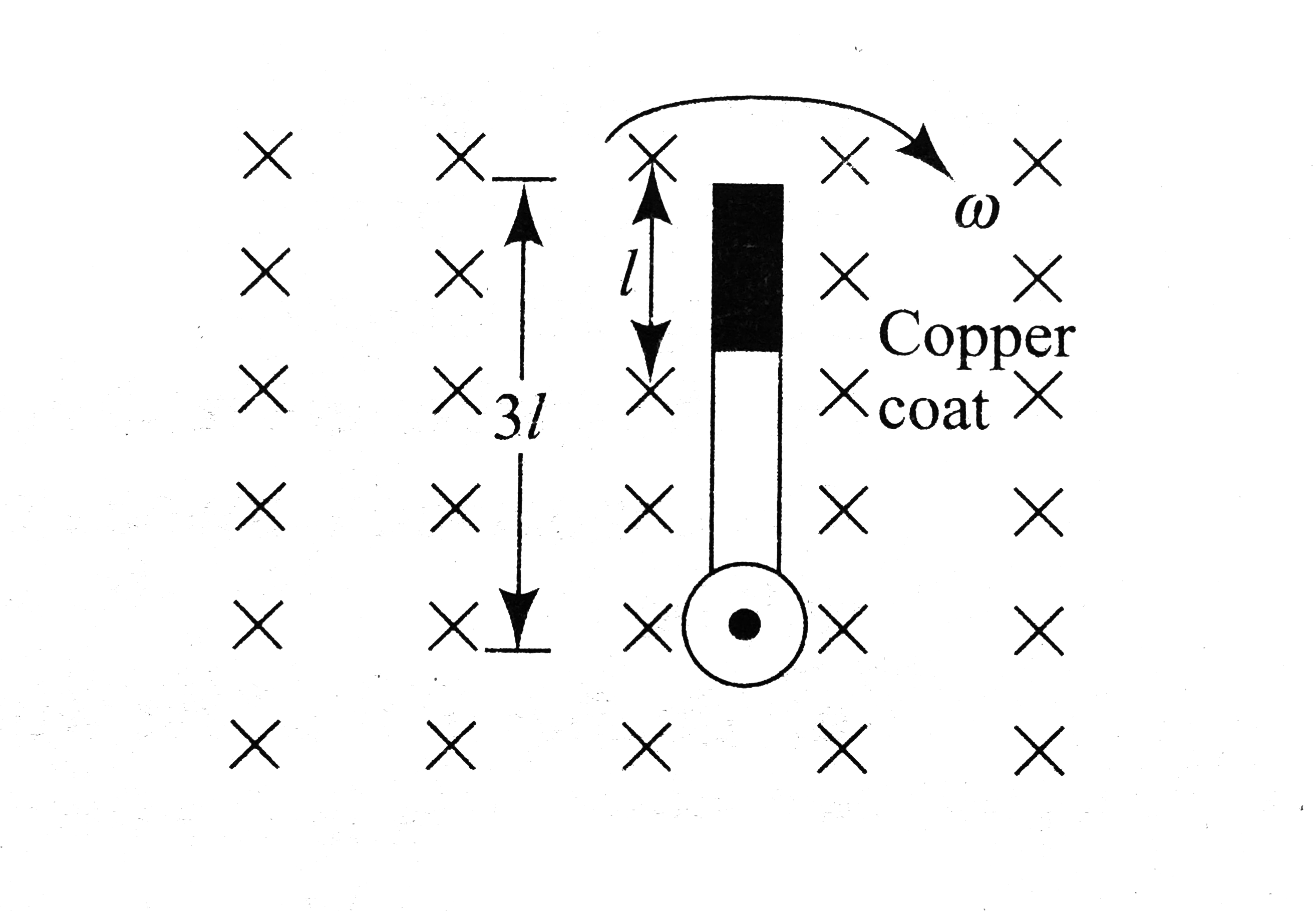
View SolutionA conducting rod of length l is rotating with constant angular velocity ω about point O in a uniform magnetic field B as shown in the figure . What is the emf induced between ends P and Q ?

View SolutionA rod AB moves with a uniform velocity v in a uniform magnetic field as shown in figure

View Solution
