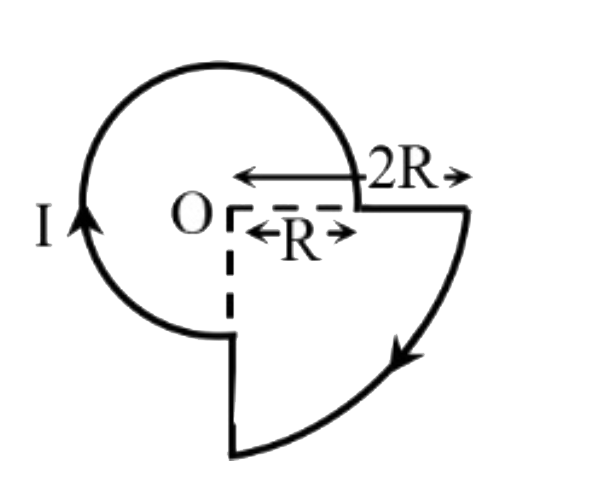
In given figure, the current (/) is flowing through straight wire annd divided equally in two loops as shown in the figure. The magnitude field intensity at center (O) is
Zero
⎛⎜ ⎜⎝μ0/8⎡⎣1r2−1r1⎤⎦⎞⎟ ⎟⎠
⎛⎜ ⎜⎝μ0/4π⎡⎣π2r2−π2r1−1r1⎤⎦⎞⎟ ⎟⎠
⎛⎜ ⎜⎝μ0/4π⎡⎣π2r2−π2r1+πr1⎤⎦⎞⎟ ⎟⎠
To solve the problem of finding the magnetic field intensity at the center (O) due to the current flowing through the wire and the loops, we can follow these steps:
1. Identify the Current Distribution:
The total current I is flowing through a straight wire and is divided equally into two loops. Therefore, the current in each loop is I2.
2. Magnetic Field Due to Each Loop:
For a semicircular loop, the magnetic field at the center can be calculated using the formula:
B=μ0I4R
where R is the radius of the loop.
3. Calculate Magnetic Field for Loop 1 (Radius r1):
The magnetic field at the center O due to the upper half of loop 1 is:
B1=μ0(I2)4r1=μ0I8r1
4. Calculate Magnetic Field for Loop 2 (Radius r2):
Similarly, the magnetic field at the center O due to the upper half of loop 2 is:
B2=μ0(I2)4r2=μ0I8r2
5. Magnetic Field Due to the Straight Wire:
The magnetic field at point O due to the straight wire is given by:
B3=μ0I4πr1
6. Total Magnetic Field at Center O:
The total magnetic field at point O is the vector sum of the magnetic fields due to the two loops and the straight wire. Since the magnetic fields due to the loops are in opposite directions to that of the straight wire, we can write:
Btotal=B3−B1−B2
Substituting the values we calculated:
Btotal=μ0I4πr1−μ0I8r1−μ0I8r2
7. Simplifying the Expression:
To combine these terms, we can factor out μ0I:
Btotal=μ0I(14πr1−18r1−18r2)
Now, finding a common denominator and simplifying gives us the final expression for the total magnetic field intensity at center O.
Final Result:
Btotal=μ0I4π(π2r2−π2r1−1r1)
The total current I is flowing through a straight wire and is divided equally into two loops. Therefore, the current in each loop is I2.
For a semicircular loop, the magnetic field at the center can be calculated using the formula:
B=μ0I4R
where R is the radius of the loop.
The magnetic field at the center O due to the upper half of loop 1 is:
B1=μ0(I2)4r1=μ0I8r1
Similarly, the magnetic field at the center O due to the upper half of loop 2 is:
B2=μ0(I2)4r2=μ0I8r2
The magnetic field at point O due to the straight wire is given by:
B3=μ0I4πr1
The total magnetic field at point O is the vector sum of the magnetic fields due to the two loops and the straight wire. Since the magnetic fields due to the loops are in opposite directions to that of the straight wire, we can write:
Btotal=B3−B1−B2
Substituting the values we calculated:
Btotal=μ0I4πr1−μ0I8r1−μ0I8r2
To combine these terms, we can factor out μ0I:
Btotal=μ0I(14πr1−18r1−18r2)
Now, finding a common denominator and simplifying gives us the final expression for the total magnetic field intensity at center O.
Btotal=μ0I4π(π2r2−π2r1−1r1)
Similar Questions
Knowledge Check
- Question 1 - Select One
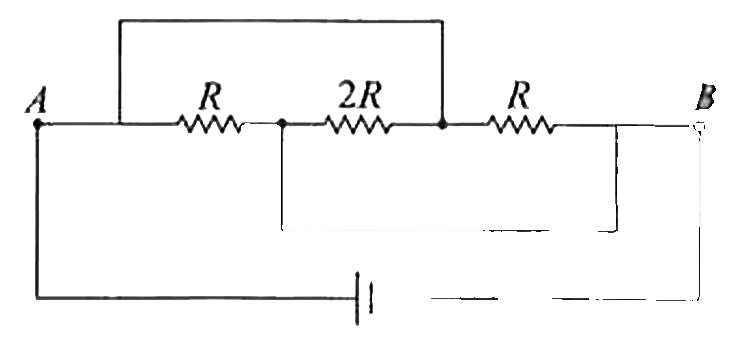
In the circuit shown in figure the current flowing through 25 V cell is
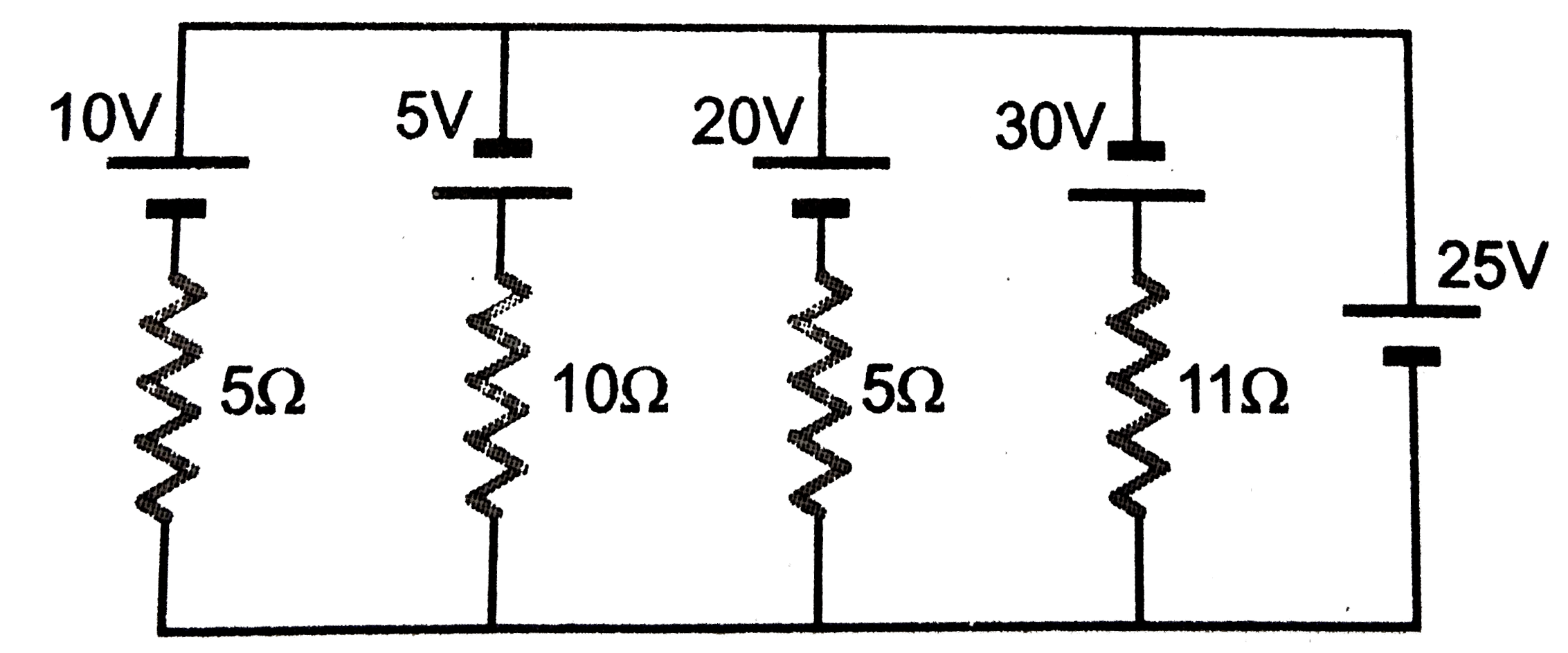 A7.2AB10AC12AD14.2A
A7.2AB10AC12AD14.2A - Question 2 - Select One
In the circuit shown in figure the current flowing through 25 V cell is
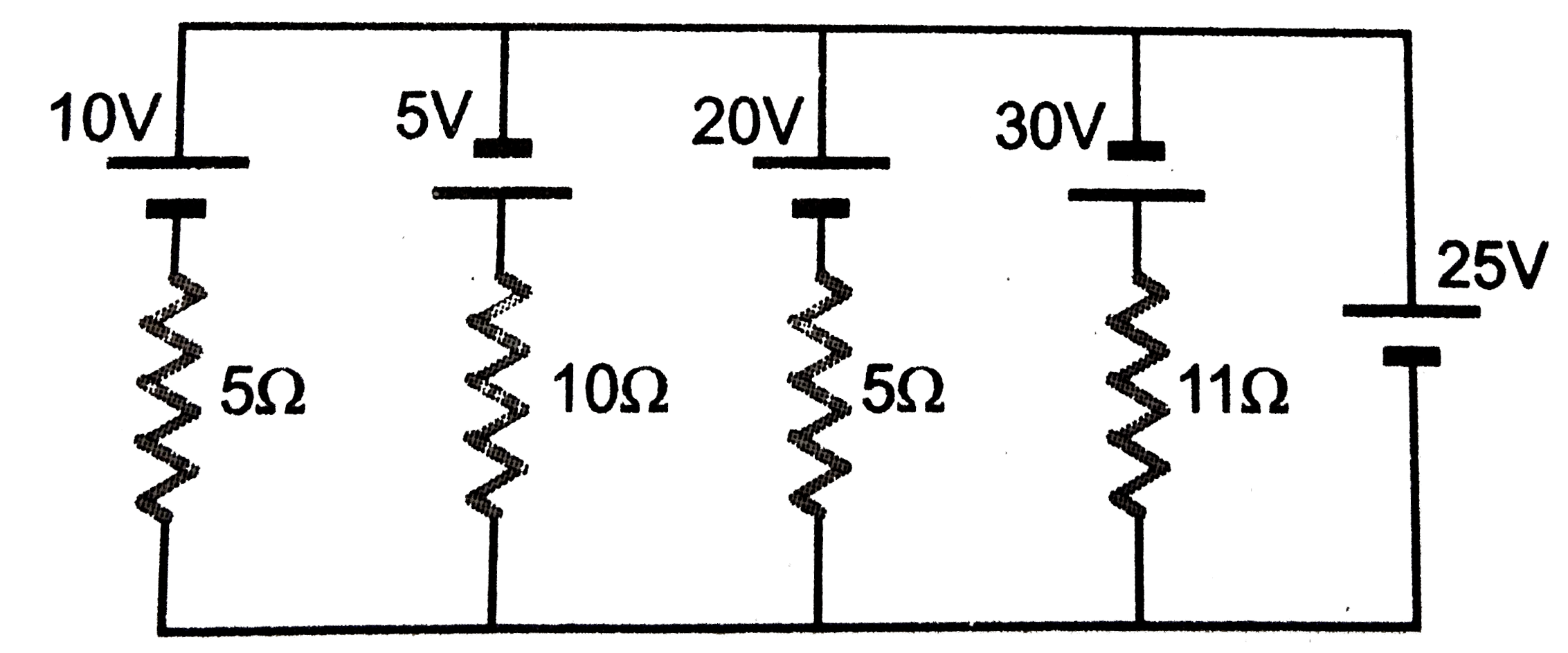 A7.2AB10AC12AD14.2A
A7.2AB10AC12AD14.2A
A current I is flowing through the loop , as shown in the figure . The magnetic field at centre O is
 View Solution
View SolutionA long wire carrying current 'I' is bent into the shape as shown in the figure. The net magnetic field intensity at the centre 'O' is
 View Solution
View SolutionA current - carrying loop is shown in the figure. The magnitude of the magnetic field produced at a point O is
 View Solution
View SolutionA current l flows through a closed loop as shown in figure .The magnetic field at the centre O is
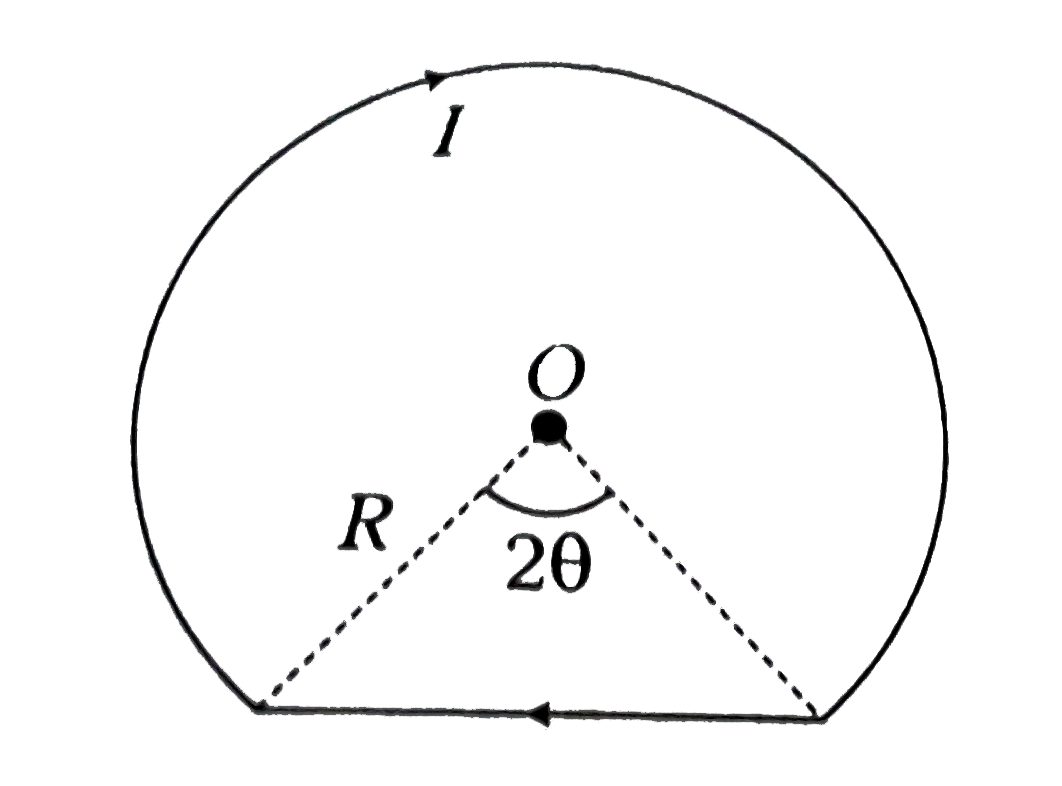 View Solution
View Solutiona straight wire current element is carrying current 100 A as shown in figure. the magnitude of magnetic field at a point P.
 View Solution
View SolutionFind the mutual inductance of a straight long wire and a rectangular loop, as shown in the figure.
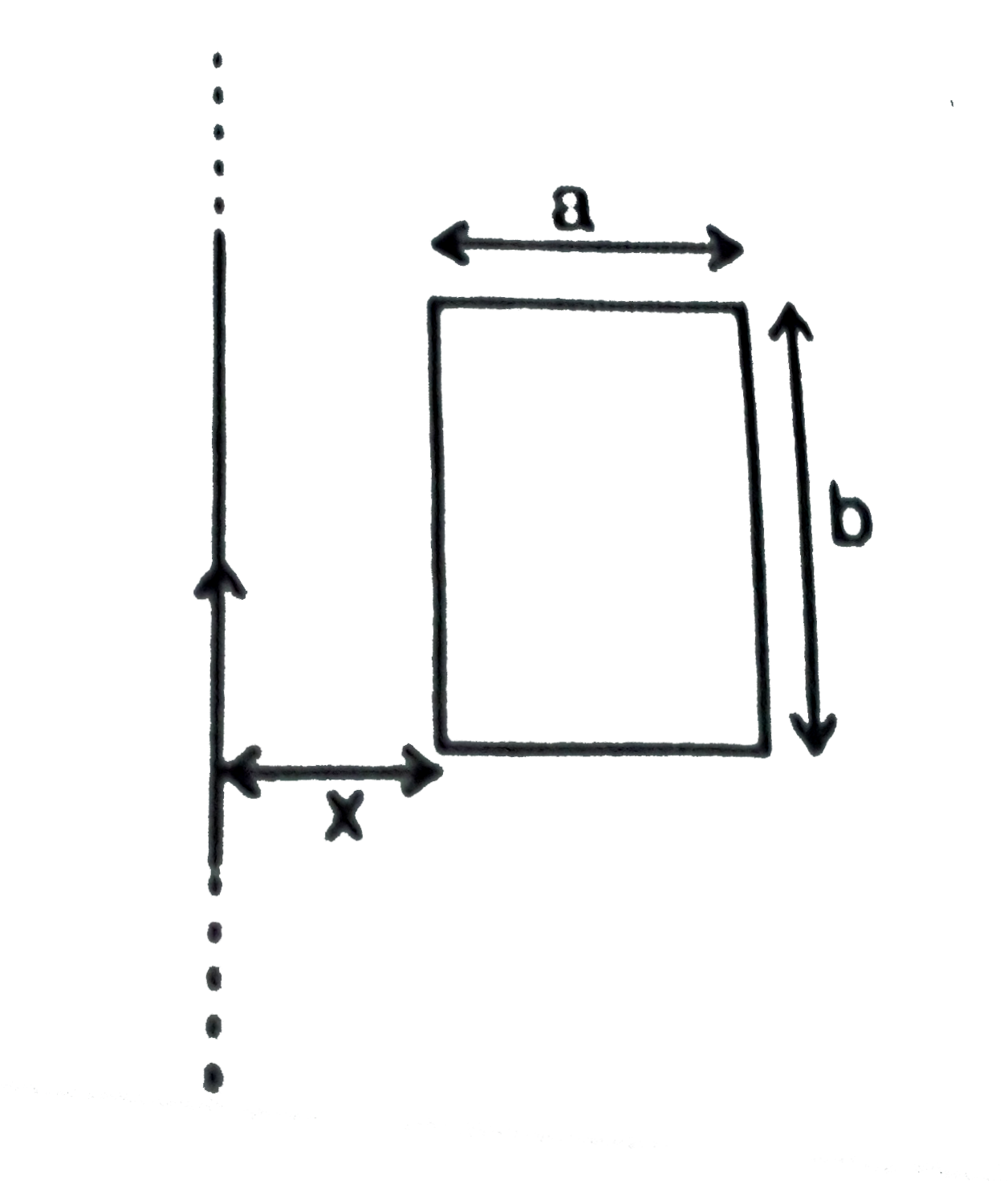 View Solution
View Solution