Two infinite long wire A and B are separated at a and current are I1 and I2 respectively. The distance from wire B where net magnetic field zero is
aI1I1−I2
aI2I1+I2
aI1I1+I2
3aI1I1−I2
To solve the problem of finding the distance from wire B where the net magnetic field is zero, we can follow these steps:
1. Understand the Setup: We have two infinite long wires, A and B, separated by a distance A. Wire A carries a current I1 and wire B carries a current I2.
2. Magnetic Field Due to a Long Wire: The magnetic field B due to an infinite long wire carrying current I at a distance d is given by the formula:
B=μ0I2πd
where μ0 is the permeability of free space.
3. Identify the Point of Interest: Let’s denote the point where the net magnetic field is zero as point X, which is at a distance x from wire B. Consequently, the distance from wire A to point X will be A−x.
4. Calculate Magnetic Fields:
- The magnetic field at point X due to wire A (current I1) is directed into the plane:
BA=μ0I12π(A−x)
- The magnetic field at point X due to wire B (current I2) is directed out of the plane:
BB=μ0I22πx
5. Set the Magnetic Fields Equal: For the net magnetic field to be zero, the magnitudes of the two magnetic fields must be equal:
BA=BB
Therefore, we can write:
μ0I12π(A−x)=μ0I22πx
6. Cancel Common Terms: The μ0 and 2π terms can be canceled from both sides:
I1A−x=I2x
7. Cross-Multiply: Cross-multiplying gives:
I1x=I2(A−x)
8. Expand and Rearrange: Expanding the right side:
I1x=I2A−I2x
Rearranging gives:
I1x+I2x=I2A
(I1+I2)x=I2A
9. Solve for x: Finally, we can solve for x:
x=I2AI1+I2
Final Answer:
The distance from wire B where the net magnetic field is zero is:
x=I2AI1+I2
B=μ0I2πd
where μ0 is the permeability of free space.
- The magnetic field at point X due to wire A (current I1) is directed into the plane:
BA=μ0I12π(A−x)
- The magnetic field at point X due to wire B (current I2) is directed out of the plane:
BB=μ0I22πx
BA=BB
Therefore, we can write:
μ0I12π(A−x)=μ0I22πx
I1A−x=I2x
I1x=I2(A−x)
I1x=I2A−I2x
Rearranging gives:
I1x+I2x=I2A
(I1+I2)x=I2A
x=I2AI1+I2
The distance from wire B where the net magnetic field is zero is:
x=I2AI1+I2
Similar Questions
Two parallel infinite wires separated by distance d carry currents as shown in figure,
_2019_CBT5_E01_052_Q01.png)
The distance from a third infinite wire be kept parallel to wire carrying current I1, the wire such that it stays in equilibrium is
View SolutionAssertion Two infinitely long wires A and B carry unequal currents both in inward direction.

Then, there is only point (excluding the ponts at infinity), where net magnetic field is zero.
Reason That point lies between points A and B.
View SolutionTwo long wires carrying current are kept crossed ( not joined at ) . The locus where magnetic field is zero is -
View SolutionCurrents of 10 A and 2A are passed through two parallel wires A and B respectuvely, in opposite direction.If the wire A is infinitely long on the wire B is 2 2m then the find the force acting on the conductor B which is situated at 10 cm distance from A
View SolutionA cylindrical long wire of radius R carries a current I uniformly distributed over the cross sectional area of the wire. The magnetic field at a distance x from the surface inside the wire is
View SolutionTwo long, straight wires, one above the other, are separated by a distance 2a and are parallel to the x-axis. Let the y-axis be in the plane of the wires in the direction form the lower wire to the upper wire. Each wire carries current I in the +x-direction. What are the magnitude and direction of the net magnetic field of the two wires at a point in the plane of wires:
(a) midway between them?
(b) at a distance a above the upper wire?
(c) at a distance a below the lower wire?
View SolutionTwo straight infinitely long and thin parallel wires are spaced 0.2m apart and carry a current of 10A each. Find the magnetic field at a point distance 0.1m from both wires in the two cases when the currents are in the (a) same and (b) opposite directions.
View SolutionTwo straight infinitely long and thin parallel wires are spaced 0.1m apart and carry a current of 10A each. Find the magnetic field at a point distance 0.1m from both wires in the two cases when the currents are in the (a) same and (b) opposite directions.
View SolutionTwo infinitely long, thin, insulated, straight wires lie in the x-y plane along the x- and y- axis respectively. Each wire carries a current I, respectively in the positive x-direction and positive y-direction. The magnetic field will be zero at all points on the straight line:
View SolutionA metallic rod of mass m and resistance R is sliding over the 2 conducting frictionless rails as shown in Fig. An infinitely long wire carries a current I0. The distance of the rails from the wire are b and a respectively.
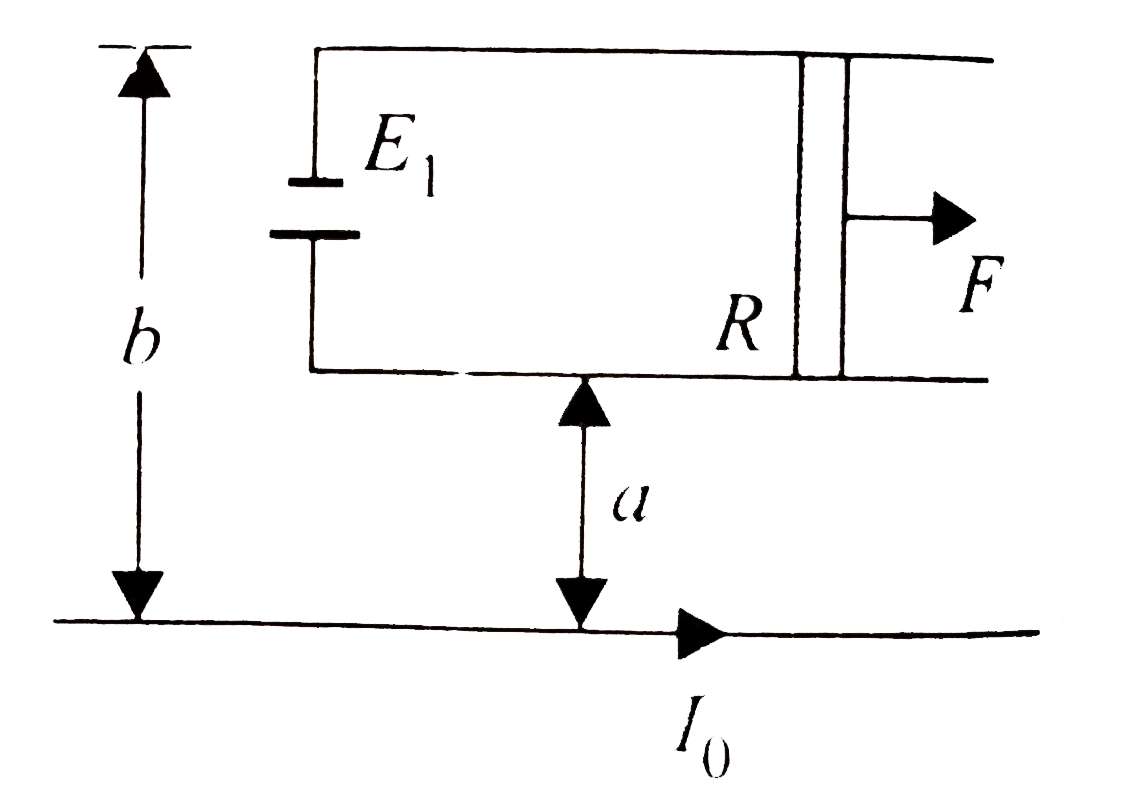
Find the value of current in the circuit if the rod slides with constant velocity v0
View Solution
