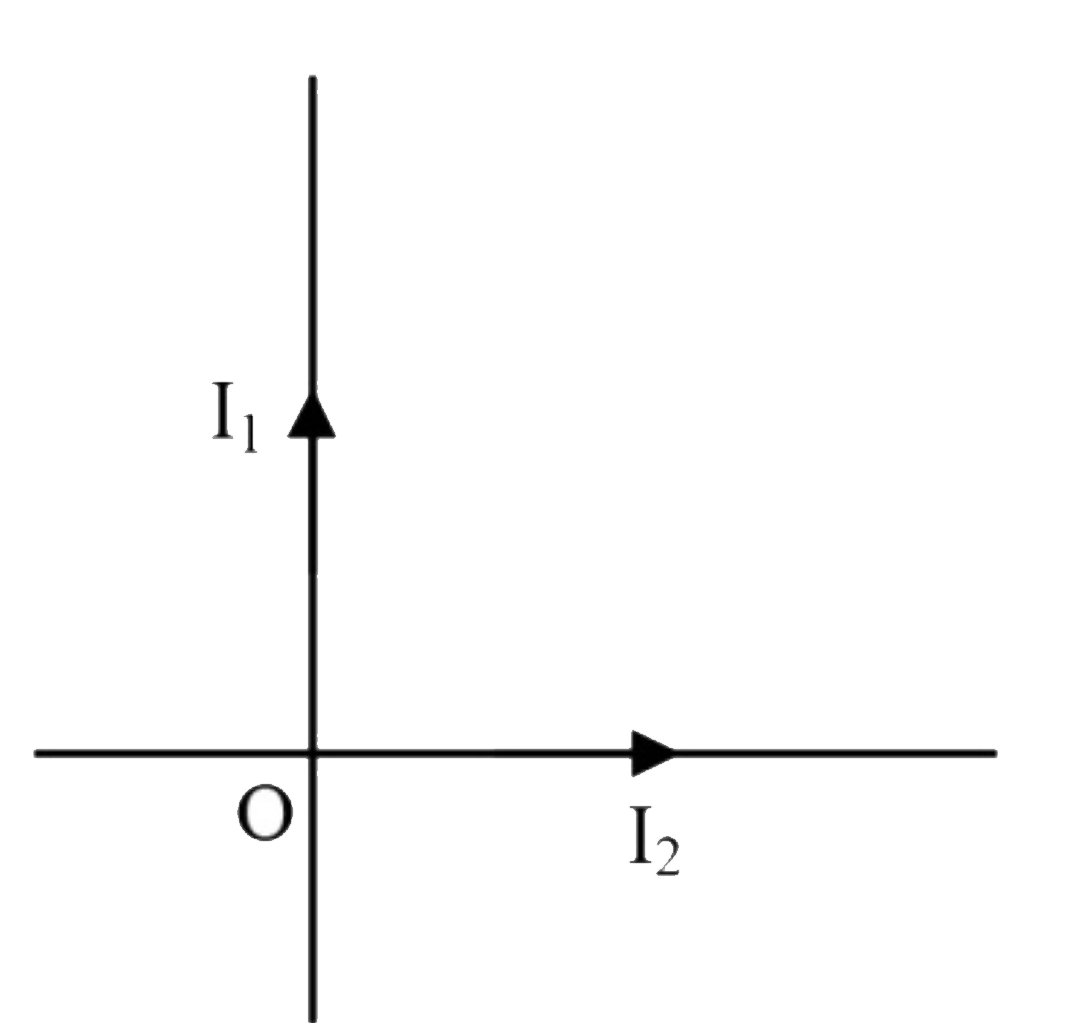
Two infinite long wire A and B are separated at a and current are I1 and I2 respectively. The distance from wire B where net magnetic field zero is
aI1I1−I2
aI2I1+I2
aI1I1+I2
3aI1I1−I2
To find the distance from wire B where the net magnetic field is zero, we can follow these steps:
Step 1: Understand the setup
We have two infinitely long parallel wires, A and B, separated by a distance A. Wire A carries a current I1 and wire B carries a current I2. We need to find the point along the line connecting the two wires where the magnetic fields due to both wires cancel each other out.
Step 2: Determine the direction of the magnetic fields
The magnetic field produced by a long straight wire carrying current I at a distance r is given by the formula:
B=μ0I2πr
where μ0 is the permeability of free space.
- If the currents in both wires are in the same direction, the magnetic fields will be in opposite directions between the wires, and the point where they cancel will be outside the segment between the two wires.
- If the currents are in opposite directions, the magnetic fields will be in the same direction between the wires, and the point where they cancel will be inside the segment between the two wires.
Step 3: Set up the equation for the magnetic fields
Assuming the currents are in opposite directions, let x be the distance from wire B where the net magnetic field is zero. The distance from wire A to this point will then be A−x.
The magnetic field due to wire A at distance A−x is:
B1=μ0I12π(A−x)
The magnetic field due to wire B at distance x is:
B2=μ0I22πx
Step 4: Set the magnetic fields equal to each other
For the net magnetic field to be zero:
B1=B2
Substituting the expressions for B1 and B2:
μ0I12π(A−x)=μ0I22πx
Step 5: Simplify the equation
Cancel out μ0 and 2π from both sides:
I1A−x=I2x
Step 6: Cross-multiply to solve for x
Cross-multiplying gives:
I1x=I2(A−x)
Expanding this:
I1x=I2A−I2x
Step 7: Rearrange the equation
Rearranging the terms gives:
I1x+I2x=I2A
(I1+I2)x=I2A
Step 8: Solve for x
Now, divide both sides by (I1+I2):
x=I2AI1+I2
Conclusion
Thus, the distance from wire B where the net magnetic field is zero is:
x=I2AI1+I2
We have two infinitely long parallel wires, A and B, separated by a distance A. Wire A carries a current I1 and wire B carries a current I2. We need to find the point along the line connecting the two wires where the magnetic fields due to both wires cancel each other out.
The magnetic field produced by a long straight wire carrying current I at a distance r is given by the formula:
B=μ0I2πr
where μ0 is the permeability of free space.
- If the currents are in opposite directions, the magnetic fields will be in the same direction between the wires, and the point where they cancel will be inside the segment between the two wires.
Assuming the currents are in opposite directions, let x be the distance from wire B where the net magnetic field is zero. The distance from wire A to this point will then be A−x.
B1=μ0I12π(A−x)
B2=μ0I22πx
For the net magnetic field to be zero:
B1=B2
Substituting the expressions for B1 and B2:
μ0I12π(A−x)=μ0I22πx
Cancel out μ0 and 2π from both sides:
I1A−x=I2x
Cross-multiplying gives:
I1x=I2(A−x)
Expanding this:
I1x=I2A−I2x
Rearranging the terms gives:
I1x+I2x=I2A
(I1+I2)x=I2A
Now, divide both sides by (I1+I2):
x=I2AI1+I2
Thus, the distance from wire B where the net magnetic field is zero is:
x=I2AI1+I2
Topper's Solved these Questions
Similar Questions
Two long current carrying wires A and B separated by 20 cm are carrying currents of 10 A and 20 A respectively in the opposite directions. Find the magnitude and direction of magnitic field at a point 10 em from both the wires.
View SolutionThere are two parallel current carrying wires X and Y as shown in figure. Find the distance of a point from wire X, where the resultant magnetic field is zero.
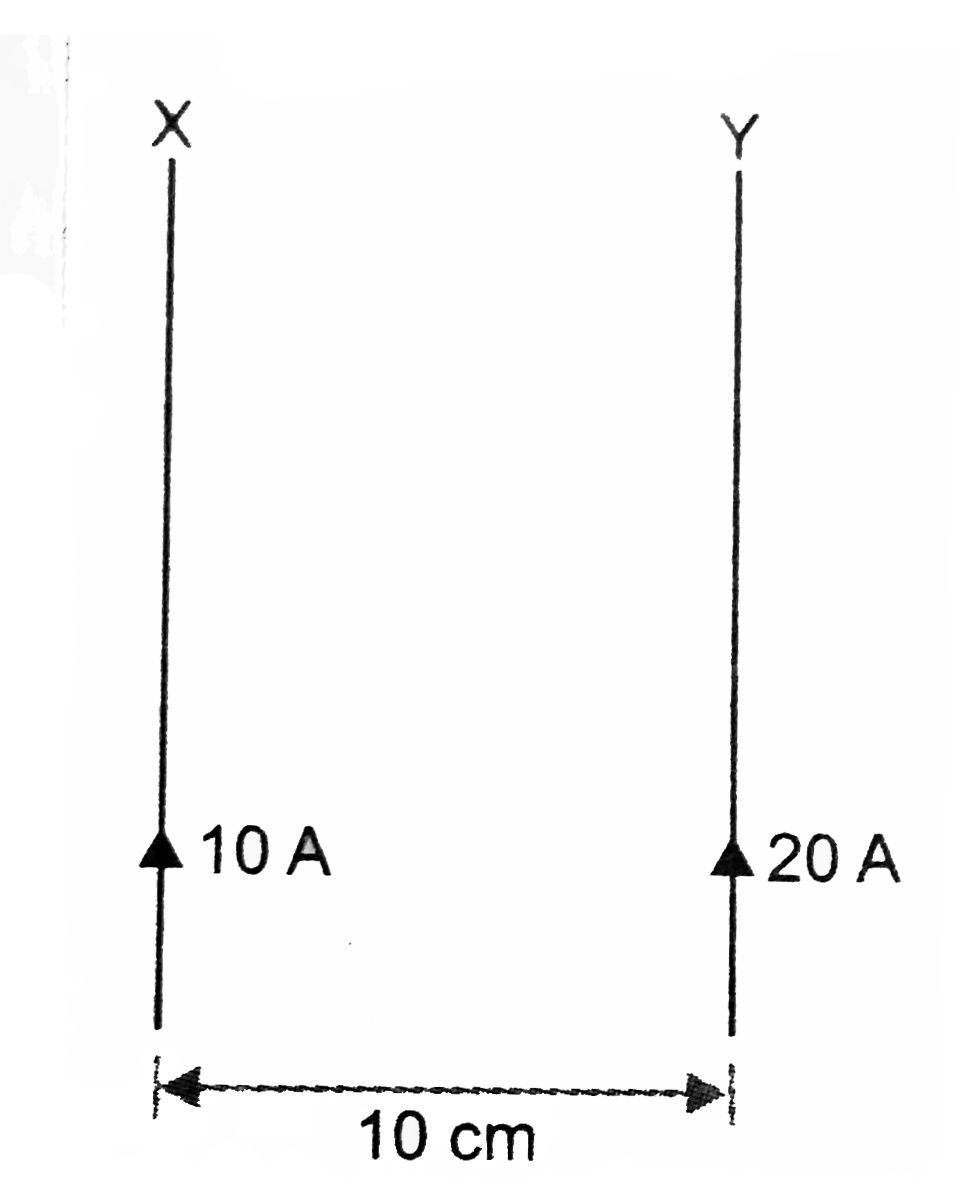
View Solution
Knowledge Check
Two long wire carrying current 2i and i are placed along co-ordinate axes x and y respectively. The locus of point where magnetic field is zero is
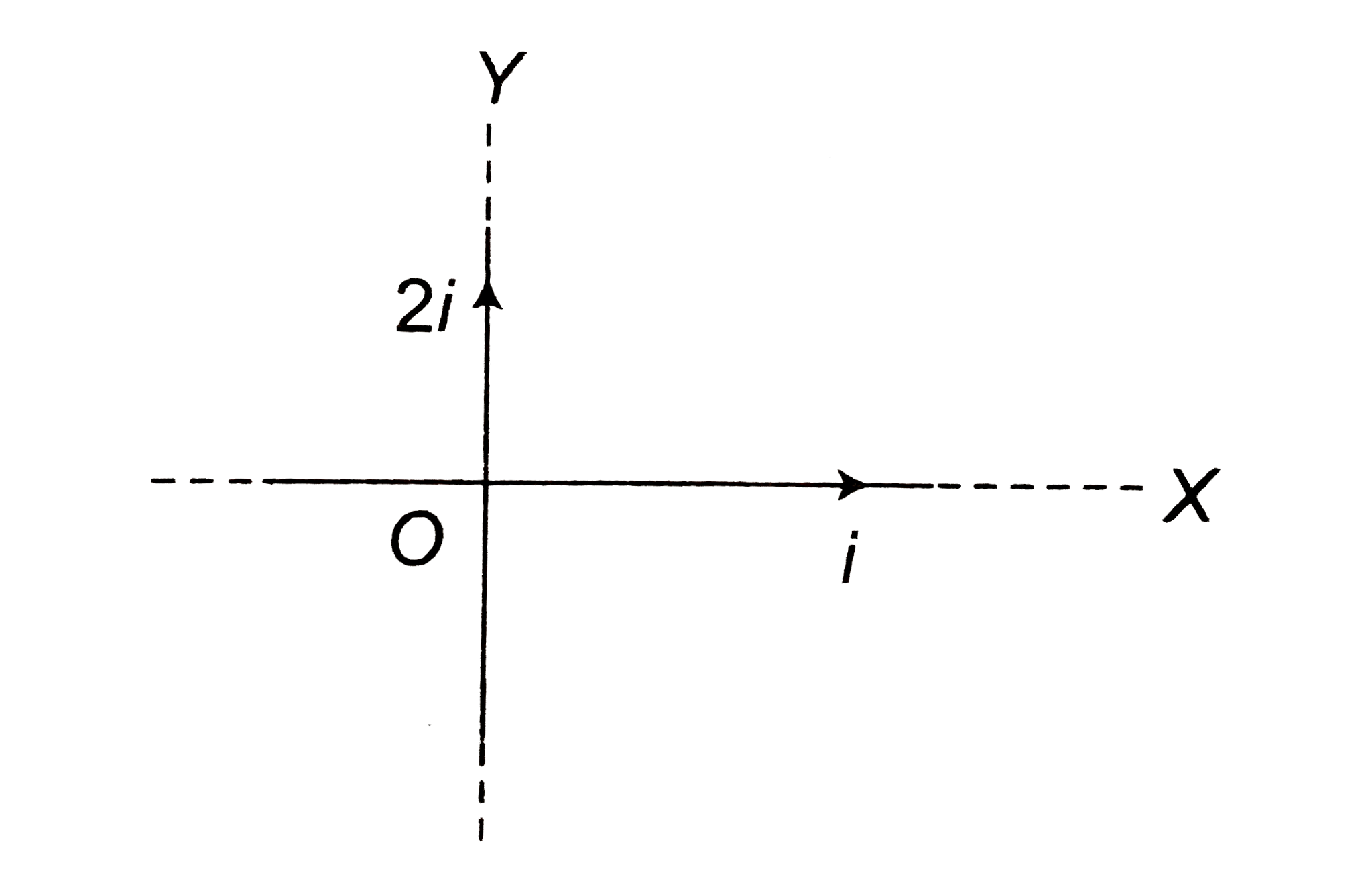 A2y−x=0Bx−2y=0Cy−x=0Dy=0
A2y−x=0Bx−2y=0Cy−x=0Dy=0Two infinitely long parallel wires carry currents of magnitudeI1 and I2 and are at a distance 4 cm apart. The magnitude of the net magnetic field is found to reach a non-zero minimum values between the two wires and 1 cm away from the first wire. The ratio of the two currents and their mutual direction is
AI2I1=9, antiparallelBI2I1=9, parallelCI2I1=3, antiparallelDI2I1=3, parallelTwo infinitely long wires each carrying current I along the same direction are made into the geometry as shown in the figure. The magnetic field at the point P is
 Aμ0IπrBμ0Ir(1π+14)CZeroDμ0I2πr
Aμ0IπrBμ0Ir(1π+14)CZeroDμ0I2πr
In the figure shown two infinitely long parallel straight current carry wires are spearated by a distance d. the current in each wire is I. Points A and B are in the plane of the wires. Find the ratio of the magnetic field BA A and Bb at B.

View SolutionThere are two infinite long parallel straight current carrying wires, A and B separated by a distance r. Figure. The current in each wire is I. The ratio of magnitude of magnetic field at point P and Q when points P and Q lie in the plane of wires is:
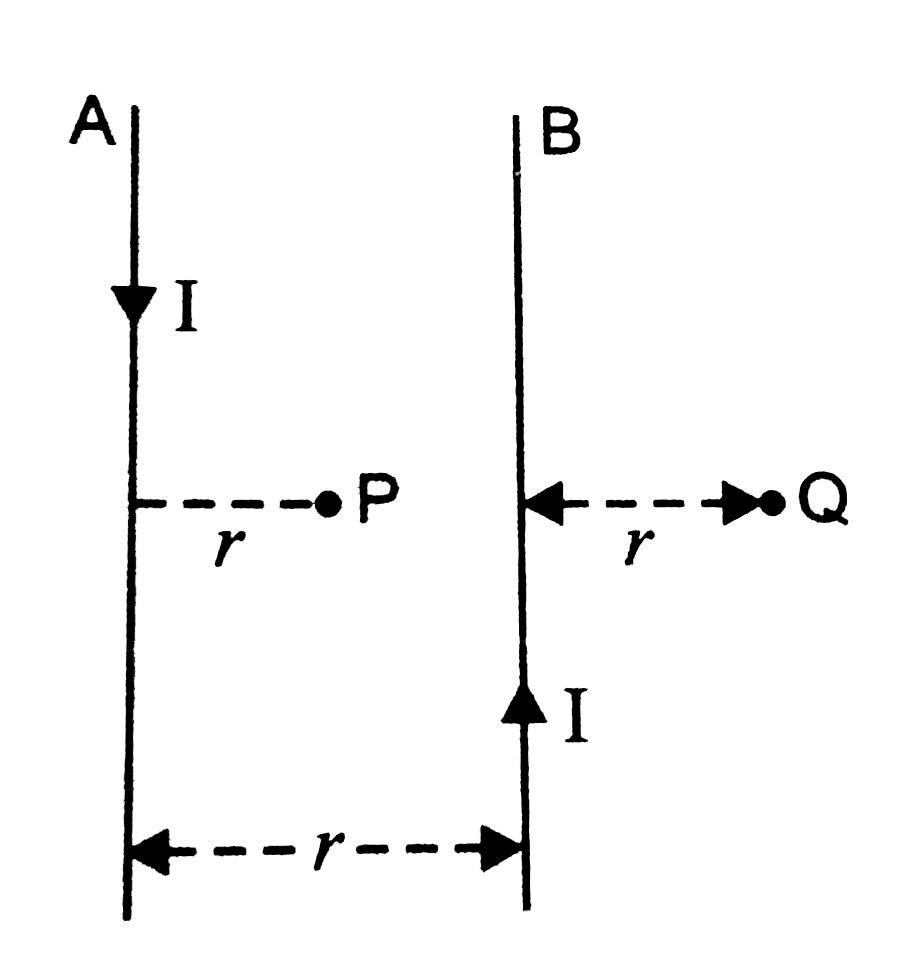
View SolutionTwo long wires carrying current are kept crossed ( not joined at ) . The locus where magnetic field is zero is -
View SolutionTwo parallel infinite wires separated by distance d carry currents as shown in figure,
_2019_CBT5_E01_052_Q01.png)
The distance from a third infinite wire be kept parallel to wire carrying current I1, the wire such that it stays in equilibrium is
View SolutionAssertion Two infinitely long wires A and B carry unequal currents both in inward direction.

Then, there is only point (excluding the ponts at infinity), where net magnetic field is zero.
Reason That point liews between points A abnd B.
View Solution
