A wire of length 1rn along x-axis carries a current 2A , is placed inside the field of →B=(3.0ˆj+4.0ˆk) tesla, then force exerted on the wire is
6ˆk+8ˆj
6ˆk−8ˆj
8ˆk−6ˆj
8ˆk−6ˆj
To find the force exerted on a wire carrying a current in a magnetic field, we can use the formula:
→F=I→L×→B
Where:
- →F is the force,
- I is the current,
- →L is the length vector of the wire,
- →B is the magnetic field vector.
Step 1: Identify the given values
- Length of the wire, L=1m (along the x-axis)
- Current, I=2A
- Magnetic field, →B=3^j+4^kT
Step 2: Write the length vector
Since the wire is along the x-axis, the length vector can be written as:
→L=1^im
Thus, the product I→L becomes:
I→L=2×1^i=2^iA m
Step 3: Calculate the cross product
Now we need to calculate the cross product →F=I→L×→B:
→F=2^i×(3^j+4^k)
Using the distributive property of the cross product:
→F=2^i×3^j+2^i×4^k
Calculating each term:
1. ^i×^j=^k
2. ^i×^k=−^j
So we get:
→F=6^k−8^j
Step 4: Write the final answer
Thus, the force exerted on the wire is:
→F=−8^j+6^kN
- →F is the force,
- I is the current,
- →L is the length vector of the wire,
- →B is the magnetic field vector.
- Length of the wire, L=1m (along the x-axis)
- Current, I=2A
- Magnetic field, →B=3^j+4^kT
Since the wire is along the x-axis, the length vector can be written as:
→L=1^im
Thus, the product I→L becomes:
I→L=2×1^i=2^iA m
Now we need to calculate the cross product →F=I→L×→B:
→F=2^i×(3^j+4^k)
Using the distributive property of the cross product:
→F=2^i×3^j+2^i×4^k
Calculating each term:
1. ^i×^j=^k
2. ^i×^k=−^j
→F=6^k−8^j
Thus, the force exerted on the wire is:
→F=−8^j+6^kN
Similar Questions
A wire of length L carries a current i along the x-axis. A magnetic field B=B0(ˆi+ˆj+ˆk) exists in the space. Find the magnitude of the magnetic force acting on the wire.
View SolutionA straight wire of length 0.5 metre and carrying a current of 1.2 ampere is placed in a uniform magnetic field of induction 2 tesla. If the magnetic field is perpendicular to the length of the wire , the force acting on the wire is
View SolutionA wire of length a'a carries a current I along the y-axis.A magnetic field exists given by
B=B0(3ˆi+2ˆj+ˆk)T
Calculate magnetic force in vector from and its magnitude
View SolutionA wire bent in the form a right angled triangle PQR, carries a current 1A. It is placed in a region of a uniform magnetic field B=0.2T. If PR=1m, the net force on the wire is

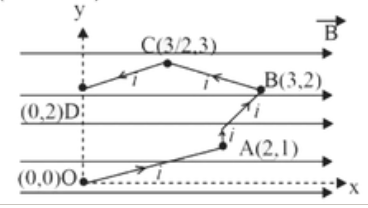
View SolutionA uniform magnetic field →B of magnitude 0.2 T exists in the plane of paper from left to right. A conducting wire, bent in an irregular manner, and carrying a current i , equal to 5A is placed in the plane of paper as shown in figure. Force acting on the wire (in Newton) is
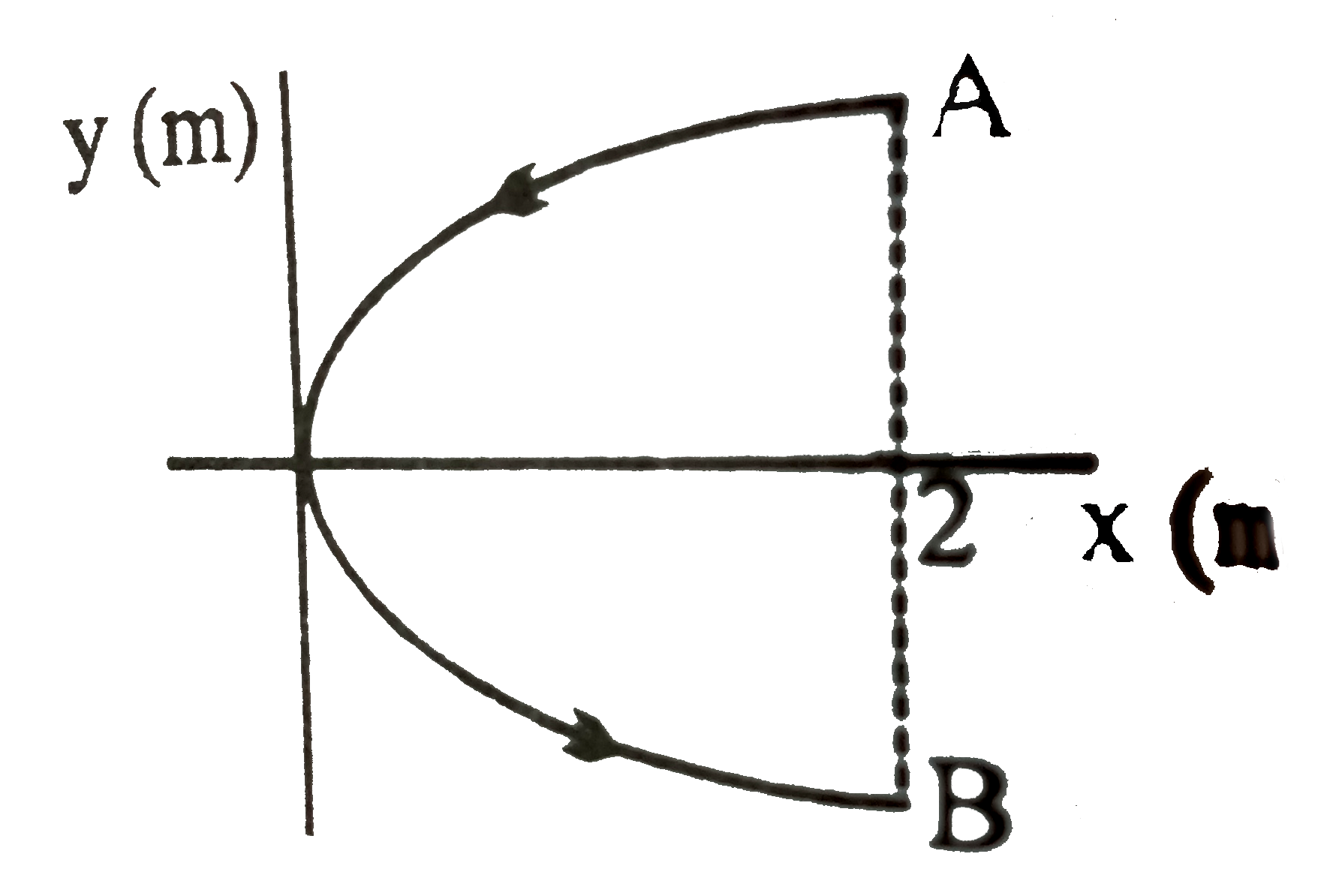
View SolutionA conducting wire bent in the from of a parabola y2=2x carries a current i=2A as shown in figure This wire is placed in a unifrom magnetic field
→B=−4ˆk Tesla The magnetic force on the wire is (newton)
 .
.
View SolutionA wire of length 1 m placed in x-z plane carries current of 1 amp. The coefficient of friction between wire and the surface is 0.2 and mass of the wire is 2. The magnetic field of strengh 2 T exists along position y direction . Then choose the correct statment .
View SolutionAn infinitely long straight wire carrying a current I1 is partially surrounded by a loop as shown in Fig. The loop has a length L, radius R, and carries a current I2 The axis of the loop coincides with the wire. Calculate the force exerted on the loop.

View SolutionThree infinitely long wires, each carrying a current 1A, are placed such that one end of each wire is at the origin, and, one of these wires is along x-axis, the other along y-axis and the third along z-axis. Magnetic induction at point (-2 m, 0, 0) due to the system of these wires can be expressed as
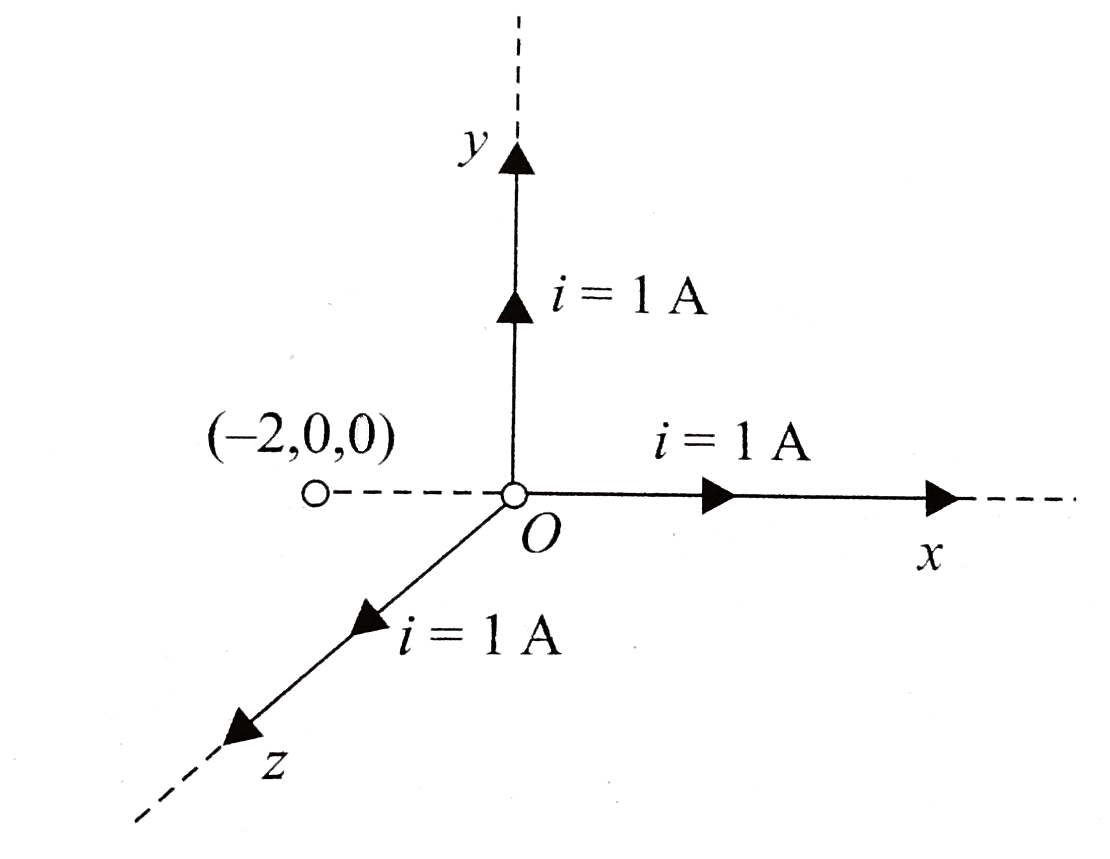
View SolutionA wire along the x-axis carries a current of 3.50A in the negative direction. Calculate the force (expressed in term of unit vectors) on a 1.00cm sectioin of the wire exerted by these magnetic fiels.
a. B=−(0.65T)ˆjb.B=+(0.56T)hatk c. B=−(0.31T)ˆj
d. B=0.33Tˆi−(0.28t)ˆk e. B=+(0.74T)ˆj−0(0.36T)ˆk
View Solution