A wire of length a'a carries a current I along the y-axis.A magnetic field exists given by
B=B0(3ˆi+2ˆj+ˆk)T
Calculate magnetic force in vector from and its magnitude
To solve the problem of finding the magnetic force on a wire carrying a current in a magnetic field, we will follow these steps:
Step 1: Identify the Given Values
We have:
- Current I
- Length of the wire L=a^j (since the wire is along the y-axis)
- Magnetic field B=B0(3^i+2^j+^k) T
Step 2: Use the Formula for Magnetic Force
The magnetic force F on a current-carrying wire is given by the formula:
F=IL×B
where × denotes the cross product.
Step 3: Substitute the Values into the Formula
Substituting the values we have:
F=I(a^j)×(B0(3^i+2^j+^k))
Step 4: Calculate the Cross Product
Now, we will calculate the cross product:
F=Ia(^j×(B0(3^i+2^j+^k)))
This simplifies to:
F=IaB0(^j×(3^i)+^j×(2^j)+^j×(^k))
Calculating each term:
- ^j×^i=−^k (since ^j crosses ^i in a clockwise direction)
- ^j×^j=0
- ^j×^k=^i
Thus, we have:
F=IaB0(−3^k+0+^i)
This simplifies to:
F=IaB0(^i−3^k)
Step 5: Write the Final Vector Form of the Force
The magnetic force in vector form is:
F=IaB0^i−3IaB0^k
Step 6: Calculate the Magnitude of the Force
To find the magnitude of the force, we use:
|F|=√(IaB0)2+(−3IaB0)2
This simplifies to:
|F|=√(IaB0)2+9(IaB0)2=√10(IaB0)2=√10IaB0
Final Answer
The magnetic force in vector form is:
F=IaB0^i−3IaB0^k
And the magnitude of the magnetic force is:
|F|=√10IaB0
We have:
- Current I
- Length of the wire L=a^j (since the wire is along the y-axis)
- Magnetic field B=B0(3^i+2^j+^k) T
The magnetic force F on a current-carrying wire is given by the formula:
F=IL×B
where × denotes the cross product.
Substituting the values we have:
F=I(a^j)×(B0(3^i+2^j+^k))
Now, we will calculate the cross product:
F=Ia(^j×(B0(3^i+2^j+^k)))
This simplifies to:
F=IaB0(^j×(3^i)+^j×(2^j)+^j×(^k))
Calculating each term:
- ^j×^i=−^k (since ^j crosses ^i in a clockwise direction)
- ^j×^j=0
- ^j×^k=^i
F=IaB0(−3^k+0+^i)
This simplifies to:
F=IaB0(^i−3^k)
The magnetic force in vector form is:
F=IaB0^i−3IaB0^k
To find the magnitude of the force, we use:
|F|=√(IaB0)2+(−3IaB0)2
This simplifies to:
|F|=√(IaB0)2+9(IaB0)2=√10(IaB0)2=√10IaB0
The magnetic force in vector form is:
F=IaB0^i−3IaB0^k
And the magnitude of the magnetic force is:
|F|=√10IaB0
Topper's Solved these Questions
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Check point
54 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Taking it together
75 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Level 2 Subjective
5 Videos
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - MCQ_TYPE
1 Videos
Similar Questions
A wire of length l carries a current I along the x-asis. A magnetic field exists which is given as →B=B0(→i+→j+→k) T. find the magnitude of the magnetic force acting on the wire.
View SolutionA wire of length L carries a current i along the x-axis. A magnetic field B=B0(ˆi+ˆj+ˆk) exists in the space. Find the magnitude of the magnetic force acting on the wire.
View SolutionA wire of length 1rn along x-axis carries a current 2A , is placed inside the field of →B=(3.0ˆj+4.0ˆk) tesla, then force exerted on the wire is
View SolutionA uniform magnetic field exists in the space B=B1ˆi+B2ˆj−B3ˆk. Find the magnetic flux through an area S, if the area S is in yz - plane.
View SolutionThe figure shows a loop of wire carrying a current i as shown. There exists a uniform magnetic field along x-axis given by →B=B0ˆi. If the length of each side is a, then
View SolutionA charge q moves with a velocity 2m/s along x- axis in a unifrom magnetic field B=(ˆi+2ˆj+3ˆk) tesla.
View SolutionA wire lying along y-axis from y=0 to y=1m carries a current of 2mA in the negative y-direction. The wire lies in a non uniform magnetic fiedl given by B=(0.3Tm)yˆi+(0.4Tm)yˆj. The magnetic force on the entire wire is
View SolutionA magnet of magnetic moment 50ˆiAm2 is placed along the x=axis in a uniform magnetic field →B=(0.5ˆi+3.0ˆj)T . What are the net force and torque experienced by the dipole ?
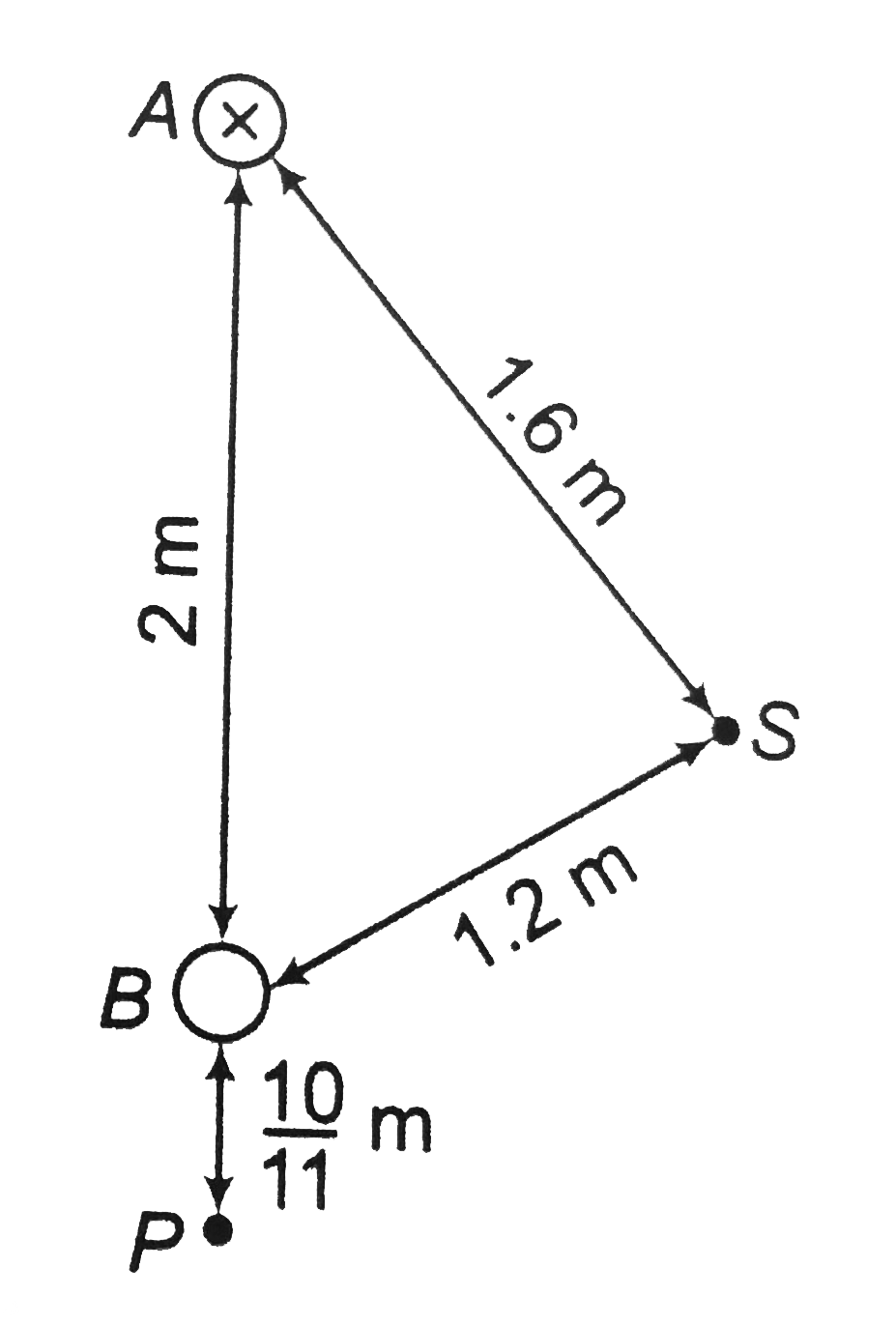
View SolutionTwo long straight parallel wieres are 2m apart, perpendicular to the plane of the paper. The wire A carries a current of 9.6A, directed into the plane of the paper. The wire B carries a current such that the magnetic field of induction at the point P, at a distance of 1011 m from the wire B, is zero. find
a. the magnitude and directiion of the current in B.
b. the magnitude of the magnetic field of induction of the pont S.
c. the force per unit length on the wire B.
View SolutionA semicircular wire of radius 5.0 cm carries a current of 5.0 A. A magnetic field B of magnitude 0.50 T exists along the perpendicular to the plane of the wire. Find the magnitude of the magnetic force acting on the wire.
View Solution
