The incorrect relation as per Ampere circuital law is
∮→B.−→dL=μ0∑l
∮→H.−→dL=∑l
∮→H.−→dL=μ0∑l
Both (1) & (2)
To determine the incorrect relation as per Ampere's Circuital Law, we need to understand what the law states and how it is applied.
1. Understanding Ampere's Circuital Law:
Ampere's Circuital Law states that the line integral of the magnetic field B around a closed loop is equal to the permeability of free space (μ₀) multiplied by the total current (I) passing through the loop. Mathematically, this is expressed as:
∮B⋅dl=μ0Ienc
where Ienc is the current enclosed by the path.
2. Identifying the Components:
- The left side of the equation, ∮B⋅dl, represents the line integral of the magnetic field.
- The right side, μ0Ienc, represents the product of the permeability of free space and the total current enclosed by the path.
3. Analyzing Possible Relations:
We need to evaluate various relations that could be presented in the question to identify which one does not conform to Ampere's Circuital Law.
4. Checking Each Relation:
- Correct Relation: If a relation states ∮B⋅dl=μ0Ienc, it is correct as it directly follows from Ampere's Circuital Law.
- Incorrect Relation: If a relation states something like ∮B⋅dl≠μ0Ienc or involves an incorrect interpretation of the current or the magnetic field, it would be incorrect.
5. Conclusion:
After evaluating the possible relations, the one that does not align with Ampere's Circuital Law will be identified as the incorrect relation.
Final Answer:
The incorrect relation as per Ampere's Circuital Law is any statement that misrepresents the relationship between the line integral of the magnetic field and the enclosed current, such as stating that ∮B⋅dl≠μ0Ienc.
---
Ampere's Circuital Law states that the line integral of the magnetic field B around a closed loop is equal to the permeability of free space (μ₀) multiplied by the total current (I) passing through the loop. Mathematically, this is expressed as:
∮B⋅dl=μ0Ienc
where Ienc is the current enclosed by the path.
- The left side of the equation, ∮B⋅dl, represents the line integral of the magnetic field.
- The right side, μ0Ienc, represents the product of the permeability of free space and the total current enclosed by the path.
We need to evaluate various relations that could be presented in the question to identify which one does not conform to Ampere's Circuital Law.
- Correct Relation: If a relation states ∮B⋅dl=μ0Ienc, it is correct as it directly follows from Ampere's Circuital Law.
- Incorrect Relation: If a relation states something like ∮B⋅dl≠μ0Ienc or involves an incorrect interpretation of the current or the magnetic field, it would be incorrect.
After evaluating the possible relations, the one that does not align with Ampere's Circuital Law will be identified as the incorrect relation.
The incorrect relation as per Ampere's Circuital Law is any statement that misrepresents the relationship between the line integral of the magnetic field and the enclosed current, such as stating that ∮B⋅dl≠μ0Ienc.
Similar Questions
Incorrect relation is
View SolutionAmpere's circuital law is given by
View SolutionState Ampere.s circuital law.
View SolutionAccording to Ampere's circuital law
View SolutionConsidering the case of a parallel plate capacitor being charged, show how one is required to generalize Ampere's circuital law to include the term due to displacment current.
View SolutionWrite equation for Ampere's circuital law for the Amperial loop as shown below
(Traverse in the direction shown by arrow mark buton it )
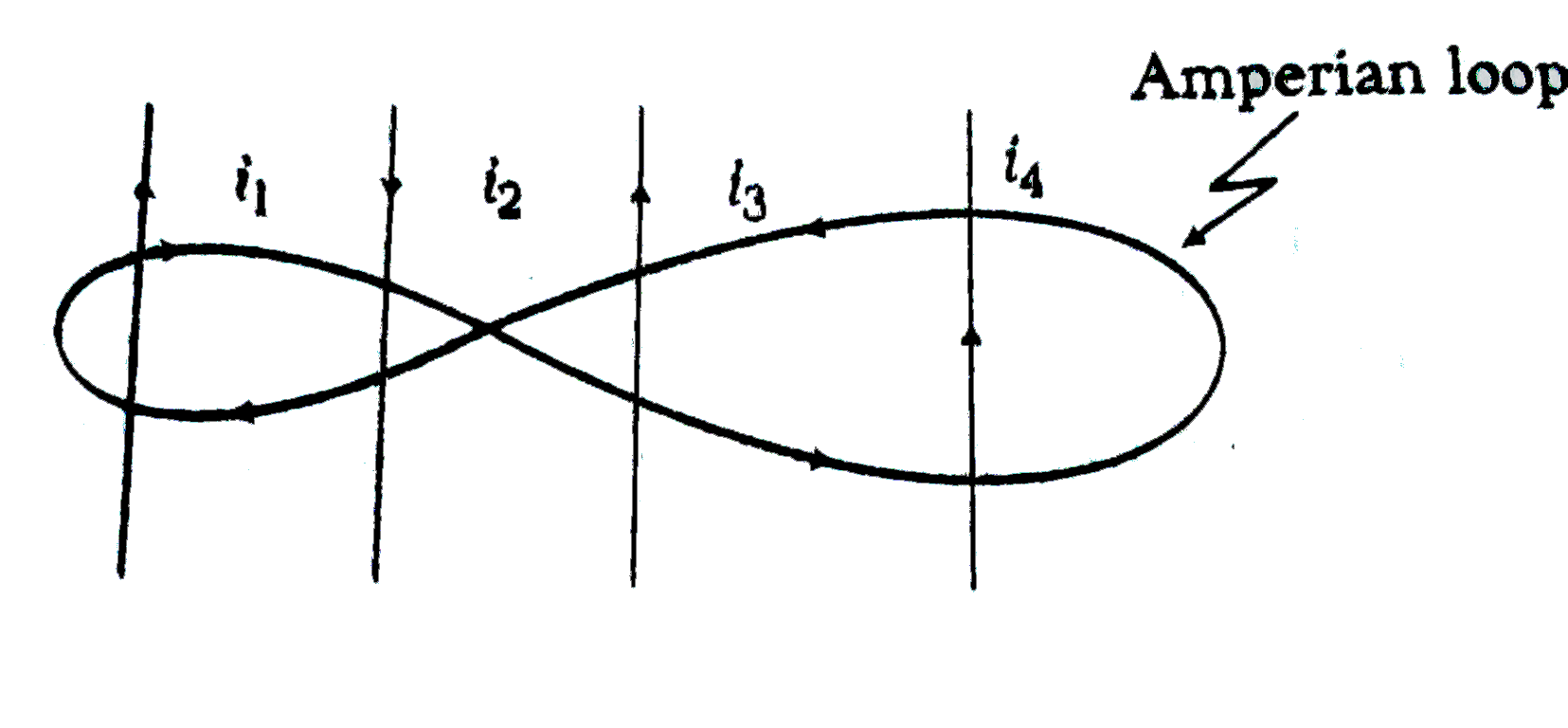
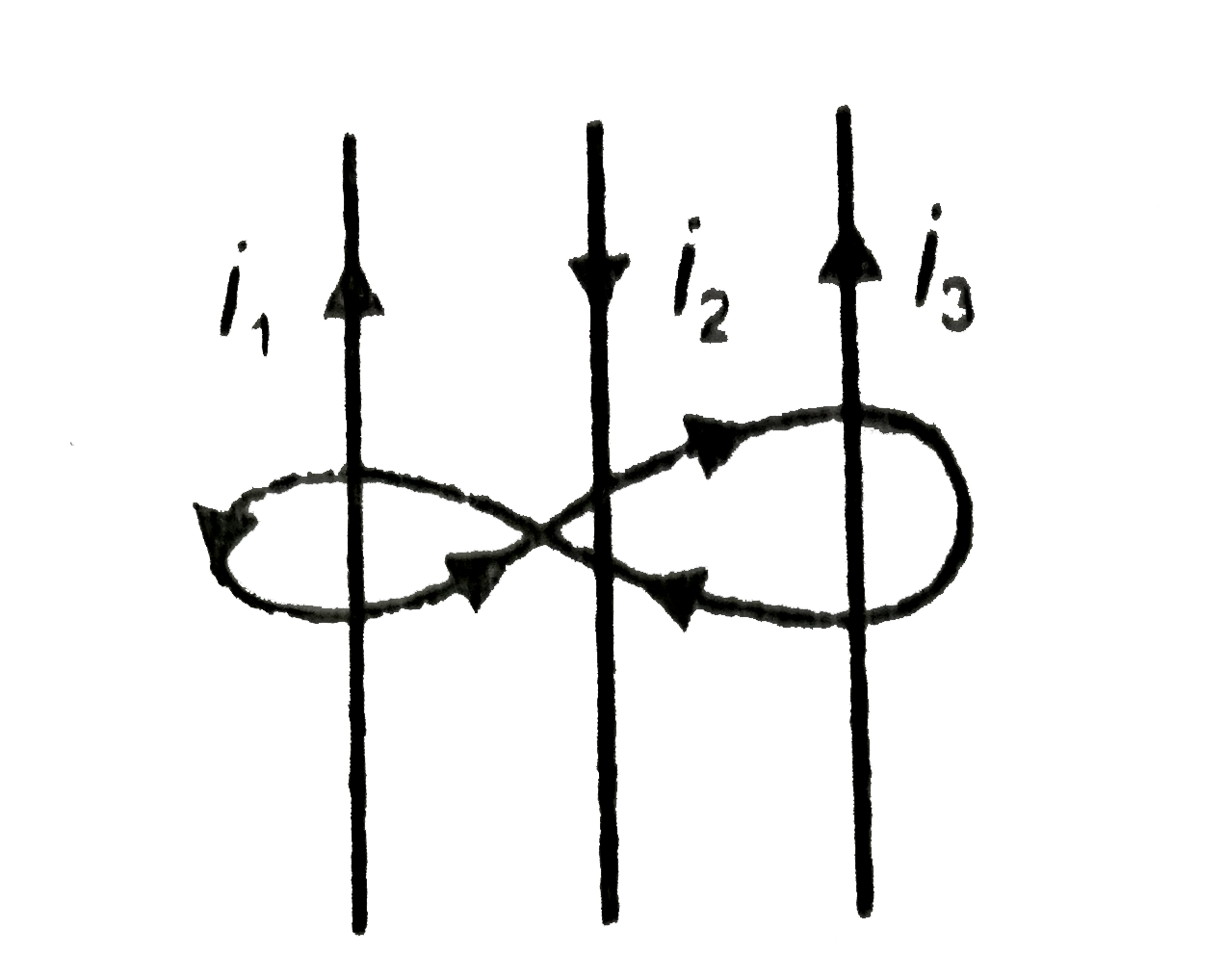
View SolutionWrite equation for Ampere's circuital law for the Amperian loop shown (traversed in the direction shown by arrow marks put on it)
View Solutionwrite the expression for the generalized form of Ampere's circuital law. Discuss its significance and describe briefly how the concept of dislacement current is explained through charing/discharging of a capacitor in an electric circuit.
View SolutionWhich of the following is incorrect in relation to an adapter molecule ?
View SolutionA: Ampere circuital law is not independent of the Biot- Savart's law.
R: Ampere's Circuital law can be derived from the Blot Savart law.
View Solution
