A mass m is connected to a massless rod of length l( and is free to rotate in vertical plane about hinged end of rod. If rod is released from horizontal position and mass "m" collides inelastically at lowest position with identical mass m, as shown in the figure, then the maximum height attained by combined mass will be
l/4
l/2
3l/4
l/8
Step by step video & image solution for A mass m is connected to a massless rod of length l( and is free to rotate in vertical plane about hinged end of rod. If rod is released from horizontal position and mass "m" collides inelastically at lowest position with identical mass m, as shown in the figure, then the maximum height attained by combined mass will be by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A uniform rod of length l and mass m is free to rotate in a vertical plane about A as shown in Fig. The rod initially in horizontal position is released. The initial angular acceleration of the rod is

View SolutionTwo point masses m are connected the light rod of length l and it is free to rotate in vertical plane as shown in figure. Calculate the minimum horizontal velocity is given to mass so that it completes the circular motion in vertical lane.
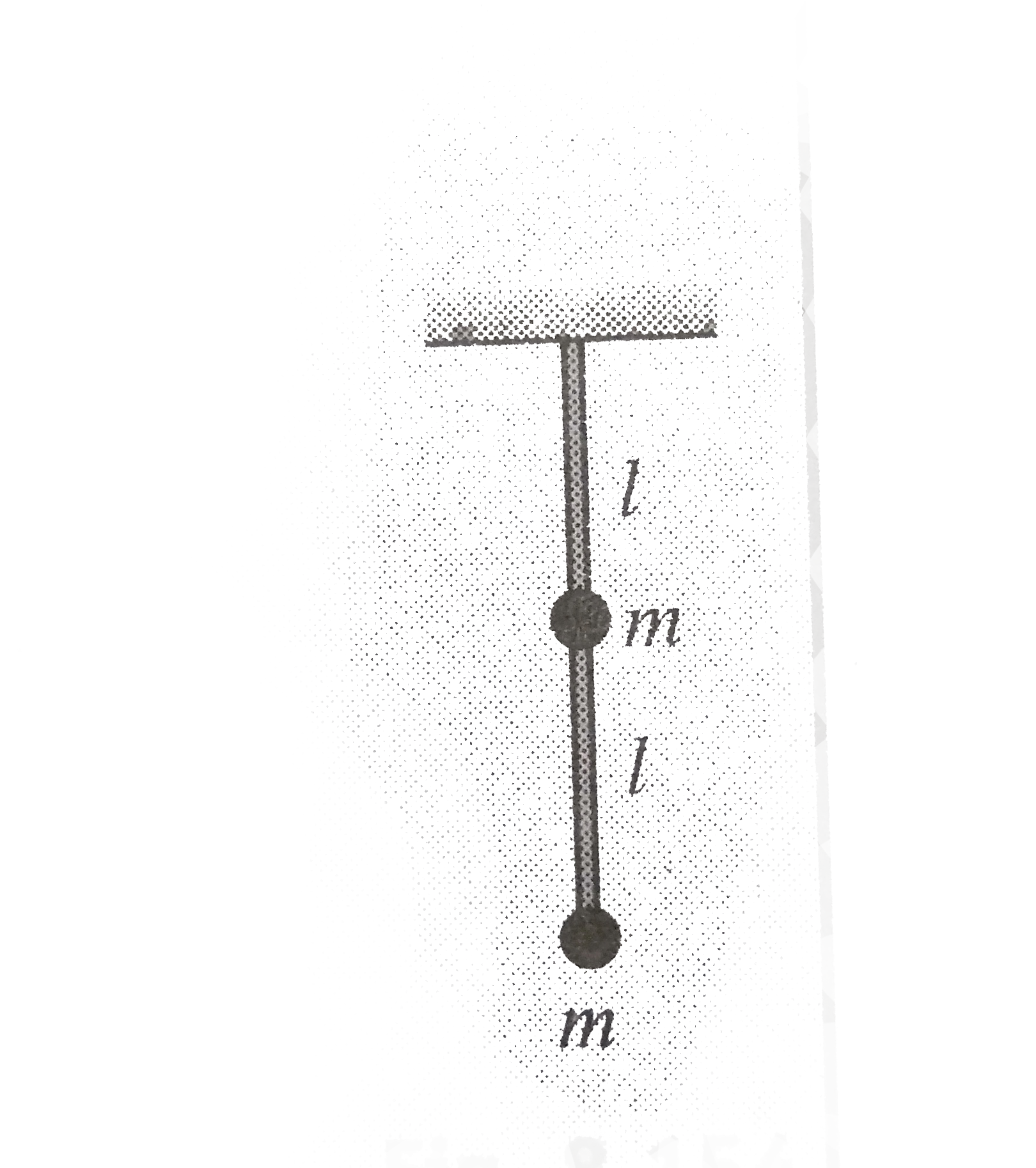
View SolutionA uniform rod of mass m and length L is free to rotate in the vertical plane about a horizontal axis passing through its end. The rod initially in horizontal position is released. The initial angular acceleration of the rod is:

View SolutionA unifrom rod of length l and mass m is free to rotate in a vertical plane about A, Fig. The rod initially in horizontal position is released. The initial angular acceleration of the rod is (MIof rod aboutAisml23)
View SolutionA L shaped rod of mass M is free to rotate in a vertical plane about axis A A as shown in figure. Maximum angular acceleration of rod is

View SolutionA rigid rod of mass m & length l is pivoted at one of its ends. If it is released from its horizontal position, find the speed of the centre of mass of the rod when it becomes vertical.
View SolutionA thin uniform rod of mass M and length L is free to rotate in vertical plane about a horizontal axis passing through one of its ends. The rod is released from horizontal position shown in the figure. Calculate the shear stress developed at the centre of the rod immediately after it is released. Cross sectional area of the rod is A. [For calculation of moment of inertia you can treat it to very thin]

View Solution
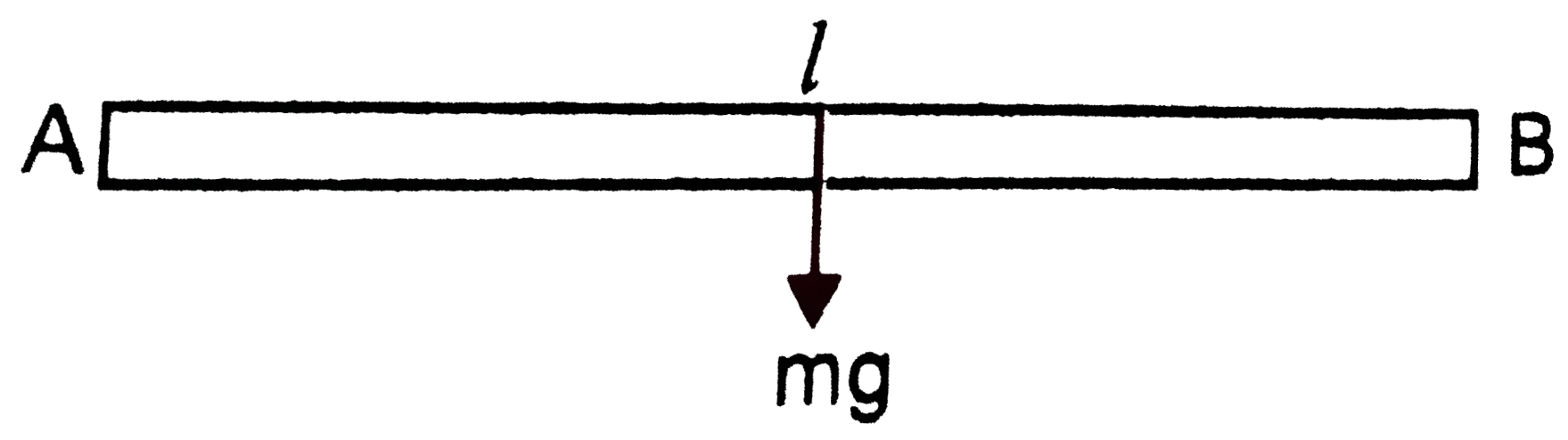
A uniform rod of length L and mass m is free to rotate about a frictionless pivot at one end as shown in figure. The rod is held at rest in the horizontal position and a coin of mass m is placed at the free end. Now the rod is released The reaction on the coin immediately after the rod starts falling is
View SolutionA uniform thin rod of length l and mass m is hinged at a distance l/4 from one of the end and released from horizontal position as shown in Fig. The angular velocity of the rod as it passes the vertical position is

View SolutionTwo particles each of mass m are attached at end points of a massless rod AB of length l. Rod is hinged at point C as shown. Rod is released from rest from horizontal position. At the instant when rod reaches its vertical position as shown, which of the following is / are correct:

View Solution
