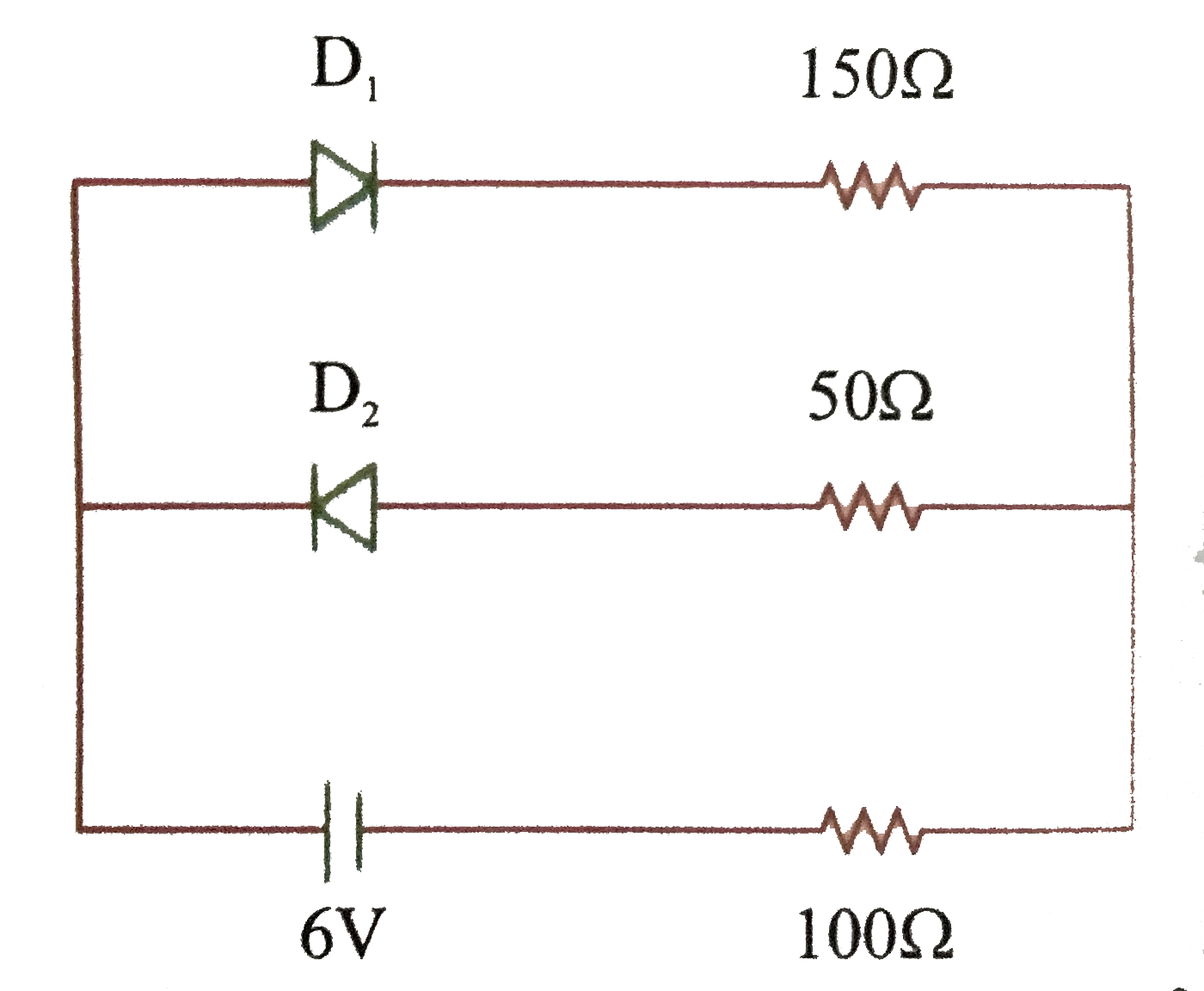
The circuit shown in figure contains two diodes each with a forward resistance of 50Ω and infinite reverse resistance.If the battery voltage is 6 v ,then the current through the 100Ω resistance is
0.04A
0.02A
0.2A
0.15A
The correct Answer is:B
To solve the problem, we need to analyze the circuit with the two diodes and the resistors. Here’s a step-by-step solution:
Step 1: Identify the configuration of the diodes
- The circuit contains two diodes, D1 and D2.
- D1 is connected in forward bias because the positive terminal of the battery is connected to the anode of D1.
- D2 is connected in reverse bias because the positive terminal of the battery is connected to the cathode of D2.
Hint: Check the orientation of the diodes with respect to the battery to determine if they are in forward or reverse bias.
Step 2: Determine the effective resistance in the circuit
- Since D1 is forward biased, it has a forward resistance of 50Ω.
- D2, being reverse biased, behaves like an open circuit and does not contribute to the current.
- The total resistance in the circuit consists of the forward resistance of D1 (50Ω) and the 100Ω resistor in series.
Hint: Remember that in a series circuit, you can simply add the resistances.
Step 3: Calculate the total resistance
- The total resistance (R_total) in the circuit is:
Rtotal=RD1+R100=50Ω+100Ω=150Ω
Hint: Ensure you only include resistances that are in the path of the current.
Step 4: Apply Ohm's Law to find the current
- According to Ohm's Law, the current (I) can be calculated using the formula:
I=VR
- Here, V = 6V (the battery voltage) and R = 150Ω (the total resistance calculated in the previous step).
Hint: Make sure to use the correct values for voltage and resistance in the formula.
Step 5: Calculate the current
- Plugging in the values:
I=6V150Ω=0.04A
Hint: Double-check your arithmetic to ensure accuracy in the calculation.
Step 6: Determine the current through the 100Ω resistor
- Since the current in a series circuit is the same through all components, the current through the 100Ω resistor (I100) is also 0.04A.
Hint: Remember that in a series circuit, the current remains constant throughout all components.
Final Answer
The current through the 100Ω resistance is 0.04 A.
---
- The circuit contains two diodes, D1 and D2.
- D1 is connected in forward bias because the positive terminal of the battery is connected to the anode of D1.
- D2 is connected in reverse bias because the positive terminal of the battery is connected to the cathode of D2.
- Since D1 is forward biased, it has a forward resistance of 50Ω.
- D2, being reverse biased, behaves like an open circuit and does not contribute to the current.
- The total resistance in the circuit consists of the forward resistance of D1 (50Ω) and the 100Ω resistor in series.
- The total resistance (R_total) in the circuit is:
Rtotal=RD1+R100=50Ω+100Ω=150Ω
- According to Ohm's Law, the current (I) can be calculated using the formula:
I=VR
- Here, V = 6V (the battery voltage) and R = 150Ω (the total resistance calculated in the previous step).
- Plugging in the values:
I=6V150Ω=0.04A
- Since the current in a series circuit is the same through all components, the current through the 100Ω resistor (I100) is also 0.04A.
The current through the 100Ω resistance is 0.04 A.
Similar Questions
The circuit shown in figure (1) Contains two diodes each with a forward resistance of 50ohm and with infinite reverse resistance. If the battery voltage is 6V, the current through the 100ohm resistance is.
 .View Solution
.View SolutionThe circuit shown in the figure contains two diodes each with a forward resistance of 50Ω and with infinite backward resistance. If the batter of 6 V is connected in the circuit, then the current through the 100Ω resistance is
View Solution
Knowledge Check
- Question 1 - Select One
The circuit shown in the figure contains two diodes each with a forward resistance of 30 Ω and with infinite backward resistance. If the battery is 3 V, the current through the 50 Ω resistance (in ampere) is
 AzeroB0.01C0.02D0.03
AzeroB0.01C0.02D0.03
The circuit showm below contains two ideal diodes, each with a forward resistance of 50Ω. If the battery voltage is 6 V, the current through the 100Ω resistance ( in Amperes) is:
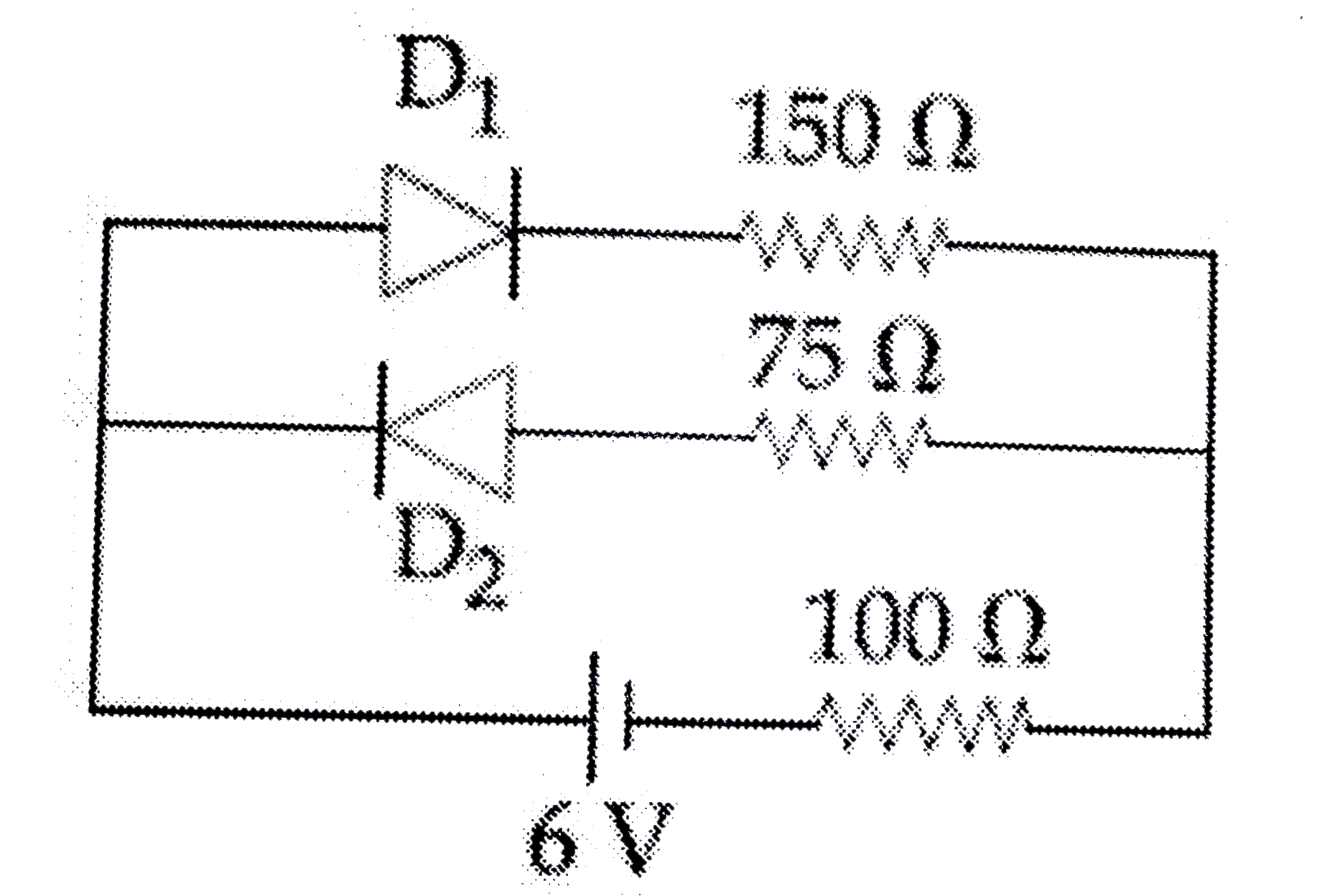 View Solution
View SolutionIn the circuit shown in figure resistance of each wire is r. Net resistance across
 View Solution
View SolutionIn the figure, the reverse breakdown voltage of a Zener diode is 5.6V, then the current IZ through the diode is
 View Solution
View SolutionThe circuit shown in the figure above consists of eight resistors, each with resistance R, and a battery with terminal voltage V and negligible internal resistance. The current flowing through the battery is n4VR, then n is
 View Solution
View SolutionIn the circuit shown in figure, each resistance is Net resistance between points A and B is
 View Solution
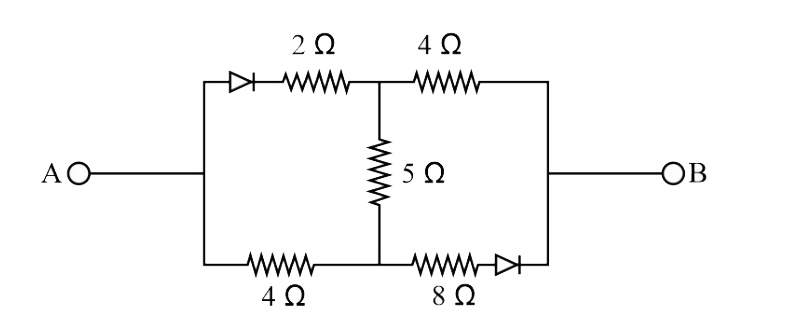
View SolutionThe part of a circuit shown in the figure consists of two ideal diodes and a few resistors. The equivalent resistance of the circuit between A and B is
 View Solution
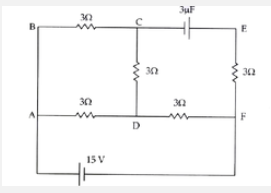
View SolutionIn the circuit shown in the figure, find the total resistance of the circuit and current in CD arm.
 View Solution
View Solution

