A population of organism growing in a habitat with limited resources
shows exponential growth
does not show any competition between individuals
shoes asymptote when population density reaches carrying capacity
is described by equation N_t=N_0e^(er)
To answer the question about a population of organisms growing in a habitat with limited resources, we can break down the process of population growth into several key steps:
1. Understanding Lag Phase:
- When a new population is introduced to a habitat, it initially experiences a lag phase. During this phase, the organisms are adjusting to their new environment, and their growth is slow.
Hint: Think of this phase as a time for the organisms to acclimatize and establish themselves.
2. Exponential Growth Phase:
- After the lag phase, the population enters the exponential growth phase. This occurs when resources are abundant, and the organisms can reproduce rapidly. The population size increases significantly during this phase.
Hint: Remember that exponential growth happens when there are plenty of resources available.
3. Resource Limitation and Competition:
- As the population continues to grow, resources (such as food, space, and water) become limited. This leads to competition among individuals for the available resources. The competition intensifies as the population density increases.
Hint: Consider how limited resources can lead to struggles among individuals in the population.
4. Carrying Capacity:
- The carrying capacity (K) is the maximum population size that the environment can sustain indefinitely. Once the population reaches this capacity, the growth rate stabilizes, and the population size levels off.
Hint: Think of carrying capacity as the "ceiling" for population growth due to resource limitations.
5. Asymptote:
- When the population reaches its carrying capacity, the growth curve becomes stabilized, which is referred to as the asymptote. At this point, the population size does not increase significantly, and the number of individuals remains relatively constant over time.
Hint: Visualize the growth curve leveling off as it approaches the carrying capacity.
6. Equation for Population Growth:
- The growth of the population can be described mathematically by the equation dndt=rN(1−NK), where:
- n = number of individuals in the population
- r = intrinsic growth rate
- K = carrying capacity
- This equation reflects how population growth slows as it approaches the carrying capacity.
Hint: Familiarize yourself with the components of the equation to understand how they relate to population dynamics.
Conclusion:
In summary, a population of organisms growing in a habitat with limited resources initially experiences a lag phase, followed by exponential growth, competition for resources, and eventually stabilizes at the carrying capacity, forming an asymptote in the growth curve. The equation governing this growth can be expressed in terms of the population size and carrying capacity.
- When a new population is introduced to a habitat, it initially experiences a lag phase. During this phase, the organisms are adjusting to their new environment, and their growth is slow.
- After the lag phase, the population enters the exponential growth phase. This occurs when resources are abundant, and the organisms can reproduce rapidly. The population size increases significantly during this phase.
- As the population continues to grow, resources (such as food, space, and water) become limited. This leads to competition among individuals for the available resources. The competition intensifies as the population density increases.
- The carrying capacity (K) is the maximum population size that the environment can sustain indefinitely. Once the population reaches this capacity, the growth rate stabilizes, and the population size levels off.
- When the population reaches its carrying capacity, the growth curve becomes stabilized, which is referred to as the asymptote. At this point, the population size does not increase significantly, and the number of individuals remains relatively constant over time.
- The growth of the population can be described mathematically by the equation dndt=rN(1−NK), where:
- n = number of individuals in the population
- r = intrinsic growth rate
- K = carrying capacity
- This equation reflects how population growth slows as it approaches the carrying capacity.
In summary, a population of organisms growing in a habitat with limited resources initially experiences a lag phase, followed by exponential growth, competition for resources, and eventually stabilizes at the carrying capacity, forming an asymptote in the growth curve. The equation governing this growth can be expressed in terms of the population size and carrying capacity.
Topper's Solved these Questions
Similar Questions
A population growing in a habitat with limited resources shows four phases of growth in the following sequence:
View SolutionAssertion : A population growing in a habitat with limited resources shows initially a lag phase, followed by phase of accelerated and deceleration and finally as asymptote, when the population density reaches the carrying capacity.
Reason : In Verhulst-Pearl Logistic growth, plot of N (population density) at time (t) results in a sigmoid curve.
View Solution
Knowledge Check
The figure below depicts life-histroy strategies for three plant species (a,b and c) along 3 axes : strength of competition with other organisms, level of distrubance in the habitat, and level of environmental stress in the habitat. Species a grows in habitats where competition among species b grown in habitats with and stress are low. Species b grows in habitats with high environmental stress but with low interspecies competition. Species c grows in highly disturbed habitats with low enviornmental stress.
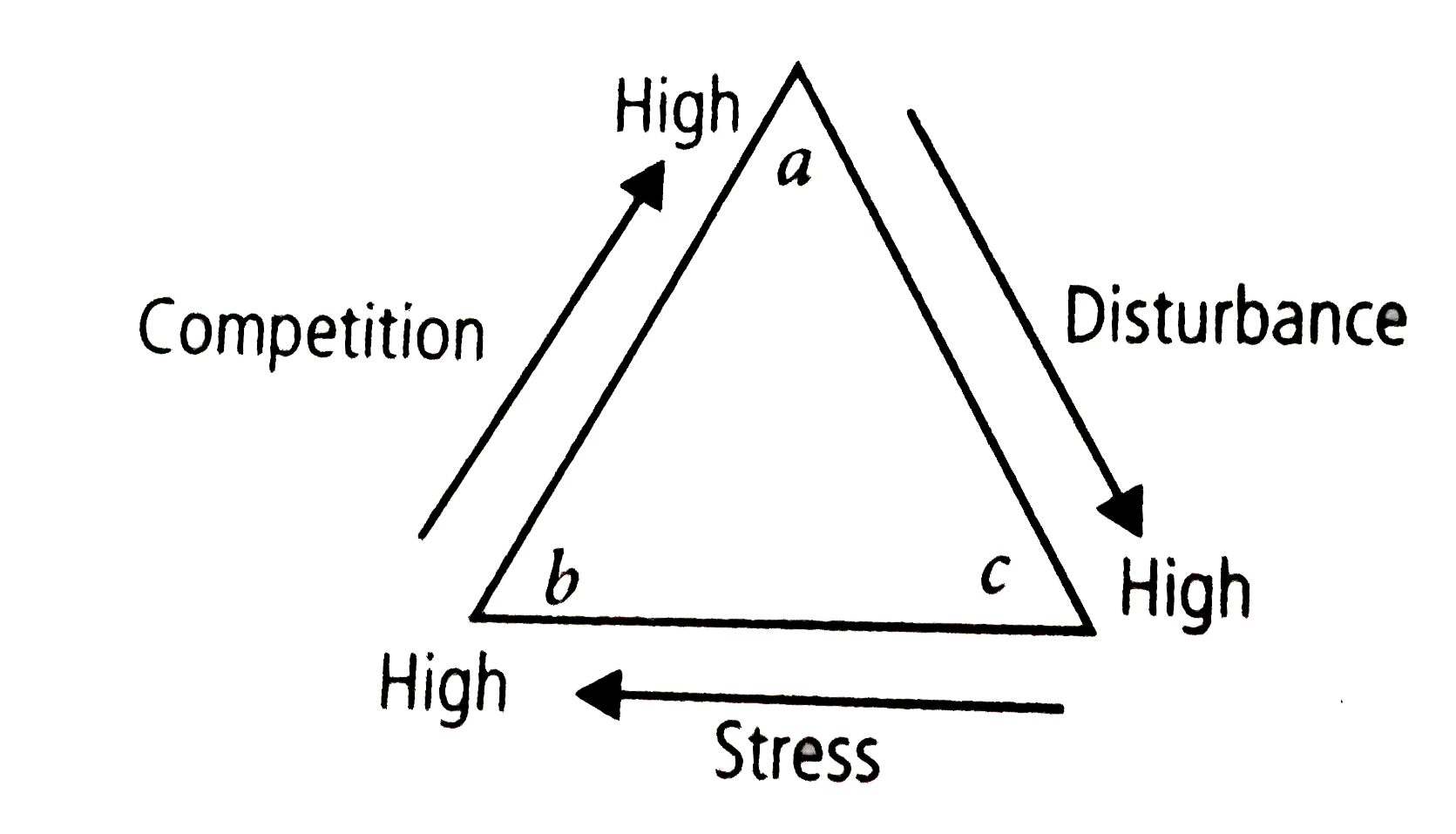 Which of the statements below is/are correct ?
Which of the statements below is/are correct ?
I. Characteristics of "a-type" plants are faster growth rate and short-lived leaves.
II. Desert annual plants are "b-type" species. they have rapid growth and produce large amount of seeds in a short time after rains.
III. Most plants belonging to "c-type" species would be herbaceous while "a-type" and "b-types" species are likely to be trees or shrubs.AOnly IIBI and IICI and IIIDII and III
which of the following option is true for verhulst Pearl logistic growth?
(A)population growth is decreased by the equation dNdt=rN[KK−N].
(B) r' represents biotic potential.
(C) applicable to a population growing in habitat with limited resources.
(D)K represents carrying capacity
View SolutionPlants growing in dry habitat are
View SolutionConservation of organisms in natural habitat is called
View SolutionResource partitioning in an environment with limited resources and interbreeding species leads to
View SolutionLargest population of organisms of any type on earth is of
View SolutionDifferent populations of the same organism present in particular geographical area are called:
View SolutionA; living organisms can exist alone
R: A population is a group of organisms of entirely different species occupying a particular area.
View Solution
