A force F=−Kx2(x≠0) acts on a particle along the X - axis. Find the work done by the force in displacing the particle from x + a to x = + 2 a . Take K as a positive constant .
Here f=−Kx2,x=+a→x=+2a
⇒W=∫2aaFdx=∫2aa−Kx2dx=∫2aa−Kx−2dx
=∫a2a+Kx−2dx=K(X−2+1−2+1)a2a
[∴∫xndx=Xn+1n+1]
=K[−1x]a2a=−K[1a−12a]∴W=−K2a
Similar Questions
A force F=−kx2(x≠0) acts on a particle in x-direction. Find the work done by this force in displacing the particle from. x=+a to x=+2a. Where, k is a positive constant.
View SolutionA force F=−kx2(x≠0) acts on a particle in x-direction. Find the work done by this force in displacing the particle from. x=+a to x=2a. Here, k is a positive constant.
View Solution
Knowledge Check
A force F=−kx2(x≠0) acts on a particle in x-direction. Find the work done by this force in displacing the particle from. x=+a to x=2a. Here, k is a positive constant.
A−k2aB−kaC−2kaD−akA force F acting on a particle varies with the position x as shown in the graph. Find the work done by the force in displacing the particle from x=−a to x=+2a.
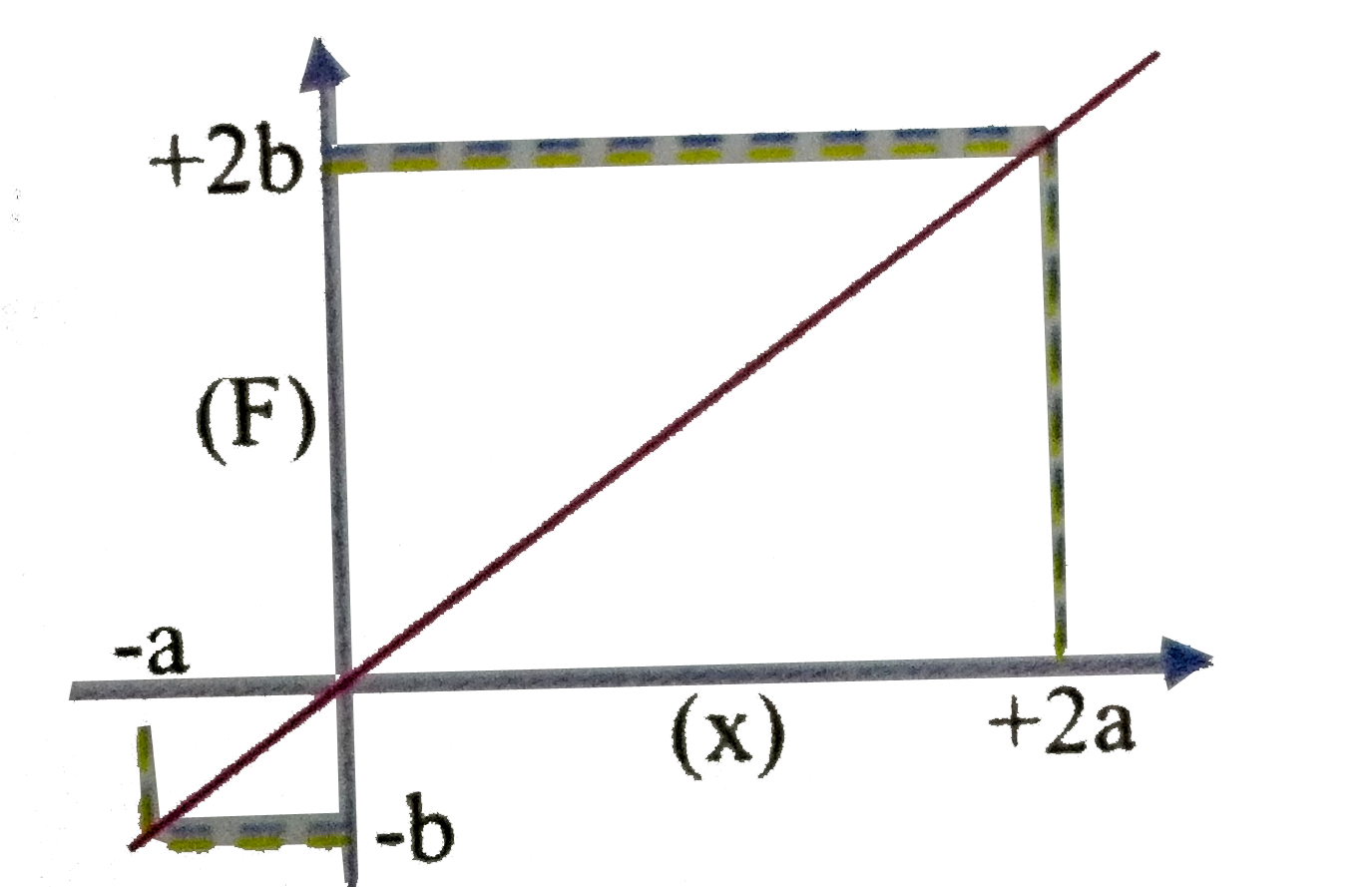 .A3ab2B4ab2C23abD24ab
.A3ab2B4ab2C23abD24abA force of F=(0.5x+12)N acts on a particle. If x is in metre, calculate the work done by the force during the displacement of the particle from x = 0 to x = 4 m
A128 JB80 JC64 JD52 J
A force F acting on a particle varies with the position x as shown in figure. Find the work done by this force in displacing the particle from
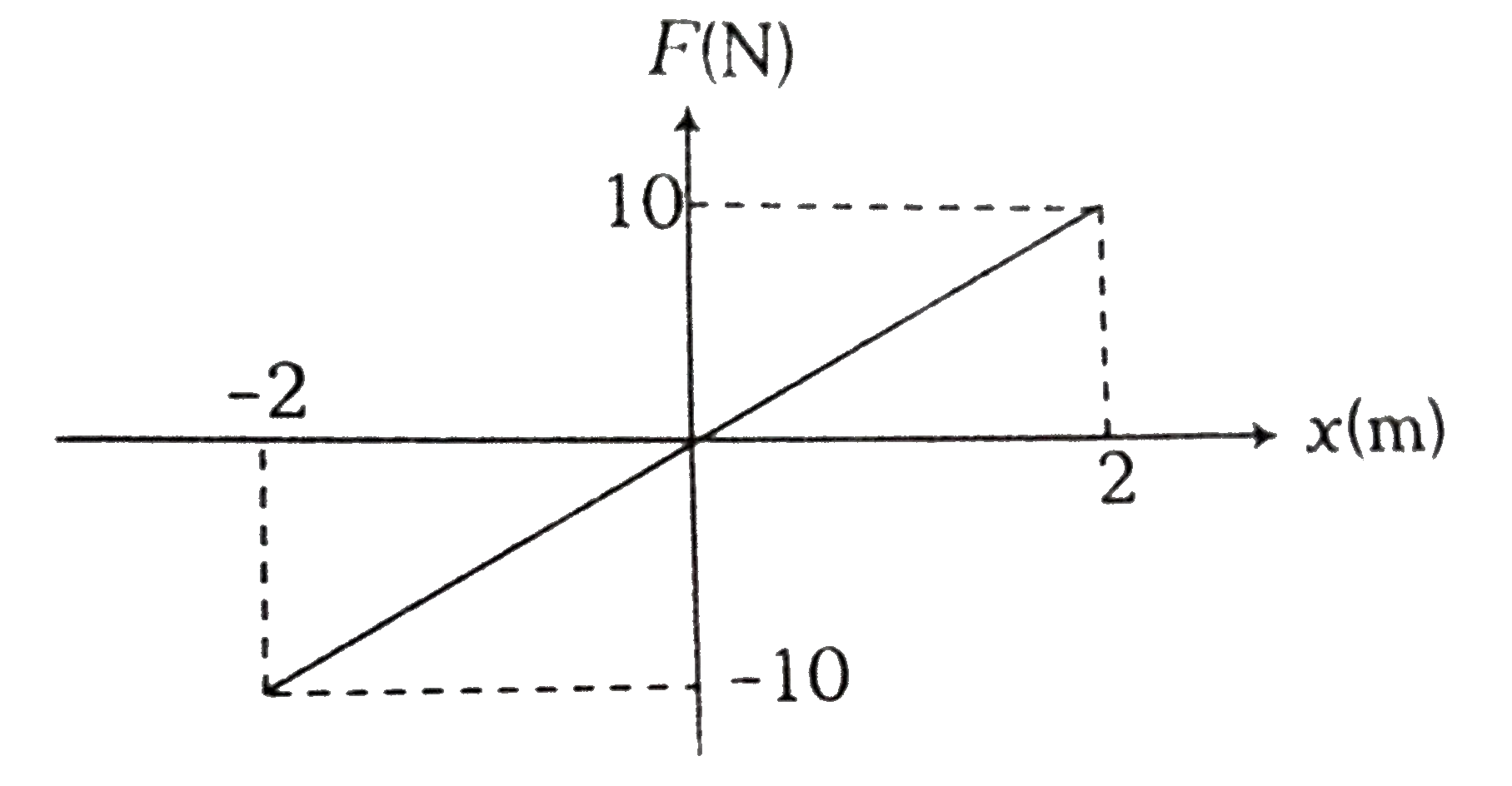
View SolutionA force F acting on a particle varies with the position x as shown in figure. Find the work done by this force in displacing the particle from

View SolutionIf force F=(2x+3x2)N is applied on a particle along x = axis, then find the work done by it during motion of particle from x = 0 to x = 2 m.
View SolutionIf force F=(2x+3x2)N is applied on a particle along x = axis, then find the work done by it during motion of particle from x = 0 to x = 2 m.
View SolutionA force F=Kx2 acts on a particle at an angle of 60° with the x–axis. the work done in displacing the particle from x1 to x2 will be –
View Solution
