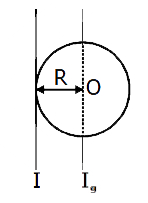
Find the moment of inertia of a sphere about a tangent to the sphere, given the moment of inertia of the sphere about any of its diameters to be $2 M R^{2} / 5$ . Where M is the mass of the sphere and R is the radius of the sphere.

Text Solution

Verified by Experts

Moment of inertia of sphere about any diameter = $\frac{2}{5} M R^{2}$
Applying theorem of parallel axes,
Moment of inertia of sphere about a tangent to the sphere = $\frac{2}{5} M R^{2} + M {(R)}^{2}$
$= \frac{7}{5} M R^{2}$ .

Updated on:21/07/2023

Find the moment of inertia of a sphere about a tangent to the sphere, while the mass of the sphere is M and the radius of the sphere is R.
A $\frac{2}{5} M R^{2}$
B $\frac{6}{5} M R^{2}$
C $\frac{4}{5} M R^{2}$
D $\frac{7}{5} M R^{2}$
If temperature increases, the moment of inertia of a solid sphere about its diameter
Aincreases
Bdecreases
Cremains unchanged
Dbecomes negative
With the increase in temperate, moment of inertia of a solid sphere about the diameter.
Adecreases
Bincreases
Cdoes not change
Dnone of these