At time t, the distance s of a particle moving in a straight line is given by s=4t2+2t. Find the average velocity between t= 2sec and t= 8 sec.Solution in Telugu
The correct Answer is:−38units/sec.
Step by step video, text & image solution for At time t, the distance s of a particle moving in a straight line is given by s= 4t^2+ 2t. Find the average velocity between t= 2sec and t= 8 sec. by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - VIKRAM PUBLICATION ( ANDHRA PUBLICATION)CHAPTER - APPLICATION OF DERIVATIVESEXERCISE - Exercise-10(f)12videos
APPLICATION OF DERIVATIVES
- BOOK - VIKRAM PUBLICATION ( ANDHRA PUBLICATION)CHAPTER - APPLICATION OF DERIVATIVESEXERCISE - Exercise-10(g)16videos
APPLICATION OF DERIVATIVES
- BOOK - VIKRAM PUBLICATION ( ANDHRA PUBLICATION)CHAPTER - APPLICATION OF DERIVATIVESEXERCISE - Exercise-10(d)8videos
APPLICATION OF DERIVATIVES
- BOOK - VIKRAM PUBLICATION ( ANDHRA PUBLICATION)CHAPTER - ADDITION OF VECTORS EXERCISE - Exercise - 4 (b)11videos
ADDITION OF VECTORS
- BOOK - VIKRAM PUBLICATION ( ANDHRA PUBLICATION)CHAPTER - DIFFERENTIATIONEXERCISE - Exercise-9(d)15videos
DIFFERENTIATION
Similar Questions
Verify Rolle's theorem for the functions (x2−1)(x−2) on [-1,2]. Find the point in the interval where the derivative vanishes.
05:13View SolutionWithout using the derivative, show that
The function f(x)=3x+7 is strictly increasing on R03:29View SolutionFind the angle between the curves x+y+2=0andx2+y2−10y=0
01:50View SolutionFind the vector equation of the line passing through the point 2¯i+3¯j+¯k and parallel to the vector 4¯i−2¯j+3¯k
01:45View SolutionIf y=2x+34x+5 then find y''.
03:40View SolutionA particle is moving in a straight line such that its distance s at any time t is given by s=t44−2t3+4t2−7. Find when its velocity is maximum and acceleration minimum.
View SolutionA particle moving along a straight line has the relation s=t3+2t+3, connecting the distance s describe by the particle in time t. Find the velocity and acceleration of the particle at t=4 sec.
08:33View SolutionPosition of a particle moving along a straight line is given by x=2t^(2)+t . Find the velocity at t = 2 sec.
01:01View Solutionएक कण सरल रेखा में गति कर रहा है । t समय पर कण द्वारा चली गई दुरी x निम्न संबंध द्वारा दी जाती है -
x=4t2+2t
समय t=12 पर कण का वेग ज्ञात कीजिए ।01:19View Solutionஆதிப்புள்ளியிலிருந்து t வினாடிகளுக்குப் பிறகு ஒரு துகள் உள்ள தூரத்தின் அளவு s=2t2+3t மீட்டர் எனும்படி நேர்க்கோட்டில் ஒரு துகள் நகர்கிறது. t=3 மற்றும் t = 6 வினாடிகளுக்கிடையே உள்ள சராசரி திசைவேகம் என்ன?
03:55View SolutionThe velocity and time graph for a particle moving in a straight line s shown in the figure. Then, the average velocity between t=4 s and t=6 s is _____
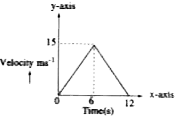 02:35View Solution
02:35View SolutionA particle is moving in a straight line such that its distance s at any time t is given by s=t44−2t3+4t2−7. Find when its velocity is maximum and acceleration minimum.
04:16View SolutionA particle is moving in a straight line such that its distance s at any time t is given by s=t44−2t3+4t2−7. Find when its velocity is maximum
02:35View SolutionA particle is moving in a straight line such that its distance at any time 't' is given by s=t^4/4-2t^3+4t^2+7 then its accelertation is minimum at t=
03:29View SolutionAt time t, the distance s of a particle moving in a straight line is given by s=4t2+2t. Find the average velocity between t= 2sec and t= 8 sec.
01:52View Solution

