What adjustments would you make for tuning a stringed instrument for it to emit a note of a desired frequency?
To tune a stringed instrument to emit a note of a desired frequency, you can follow these steps:
Step 1: Understand the Relationship Between Frequency, Tension, and Length
The frequency of a vibrating string is influenced by two main factors: the tension in the string and the length of the string.
- Tension: The frequency is directly proportional to the tension. This means that if you increase the tension of the string, the frequency will also increase.
- Length: The frequency is inversely proportional to the length of the string. If you increase the length of the string, the frequency will decrease, and if you decrease the length, the frequency will increase.
Step 2: Adjust the Tension of the String
To achieve the desired frequency:
- Use the tuning pegs or mechanisms on the instrument to increase or decrease the tension of the string.
- If the note is too low, tighten the string (increase tension).
- If the note is too high, loosen the string (decrease tension).
Step 3: Change the Length of the String
If adjusting the tension alone does not achieve the desired frequency:
- Change the vibrating length of the string by using a capo or by pressing down on the string at different frets (for instruments like a guitar).
- Shortening the length (by pressing down) will increase the frequency, while lengthening it will decrease the frequency.
Step 4: Fine-Tuning
- After making the adjustments, play the string to check if the frequency matches the desired note.
- Repeat the adjustments as necessary until the desired frequency is achieved.
Summary
To tune a stringed instrument to the desired frequency, you can:
1. Adjust the tension of the string using the tuning pegs.
2. Change the length of the string by pressing down on the frets or using a capo.
3. Fine-tune by checking the sound and making further adjustments.
---
The frequency of a vibrating string is influenced by two main factors: the tension in the string and the length of the string.
- Length: The frequency is inversely proportional to the length of the string. If you increase the length of the string, the frequency will decrease, and if you decrease the length, the frequency will increase.
To achieve the desired frequency:
- Use the tuning pegs or mechanisms on the instrument to increase or decrease the tension of the string.
- If the note is too low, tighten the string (increase tension).
- If the note is too high, loosen the string (decrease tension).
If adjusting the tension alone does not achieve the desired frequency:
- Change the vibrating length of the string by using a capo or by pressing down on the string at different frets (for instruments like a guitar).
- Shortening the length (by pressing down) will increase the frequency, while lengthening it will decrease the frequency.
- After making the adjustments, play the string to check if the frequency matches the desired note.
- Repeat the adjustments as necessary until the desired frequency is achieved.
To tune a stringed instrument to the desired frequency, you can:
1. Adjust the tension of the string using the tuning pegs.
2. Change the length of the string by pressing down on the frets or using a capo.
3. Fine-tune by checking the sound and making further adjustments.
Topper's Solved these Questions
- SOUNDBOOK - ICSECHAPTER - SOUNDEXERCISE - EXERCISE -7(B)( MULTIPLE CHOICE TYPE)
2 Videos
- SOUNDBOOK - ICSECHAPTER - SOUNDEXERCISE - EXERCISE -7(C )
47 Videos
- SOUNDBOOK - ICSECHAPTER - SOUNDEXERCISE - EXERCISE -7(A) (NUMERICALS )
14 Videos
- SIMPLE MACHINES BOOK - ICSECHAPTER - SIMPLE MACHINES EXERCISE - DIAGRAM BASED MCQ
5 Videos
- SPECIMEN PAPER (SOLVED)BOOK - ICSECHAPTER - SPECIMEN PAPER (SOLVED)EXERCISE - SECTION II
78 Videos
Similar Questions
What do you mean by pure tone? Which instrument can produce it?
View SolutionA tuning fork of frequency 256 Hz produces 4 beats per second when sounded with a stringed instrument. What is the frequency produced by the instrument?
View SolutionThe diagram in Fig. shows three ways in which a string of length I in an instrument can vibrate.
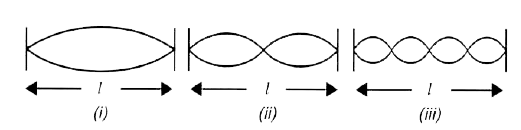
What is the ratio of frequency of vibrations in diagrams (i) and (ii) ?
View SolutionAn open pipe is 85 cm long. If the velocity of sound is 340 ms−1, find the frequency of the fundamental note of the pipe. What would be the length of a closed pipe which produces a fundamental note of the same frequency?
View SolutionAn open pipe produces fundamental note. All of a sudden one of its ends is closed. If again fundamental note is emitted, the frequency of the note will be :
View SolutionA siren emitting a sound of frequency 1000HZ moves away from you towards a cliff at a speed of 10m/s .
(a) What is the frequency of the sound you hear coming directly from the sirven ?
(b) What is the frequency of sounds you hear reflected off the cliffb ?
(c) What beat frequency would you hear ? Take the speed of sound in air as 330m/s .
View SolutionA siren emitting a sound of frequency 2000 Hz moves away from you towards a cliff at a speed of 8 m/s.
(a) What is the frequency of the sound you hear coming directly from the siren.
(b) What is the frequency of sound you hear reflected off the cliff. Speed of sound in air is 330ms.
View SolutionThe diagram in Fig. shows three ways in which a string of length I in an instrument can vibrate.
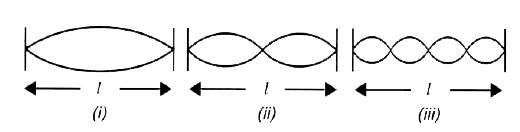
Which vibration has a frequency four times that of the first?
View SolutionAn ac generator G with an adjustable frequency of oscillation is used in the circuit, as shown.
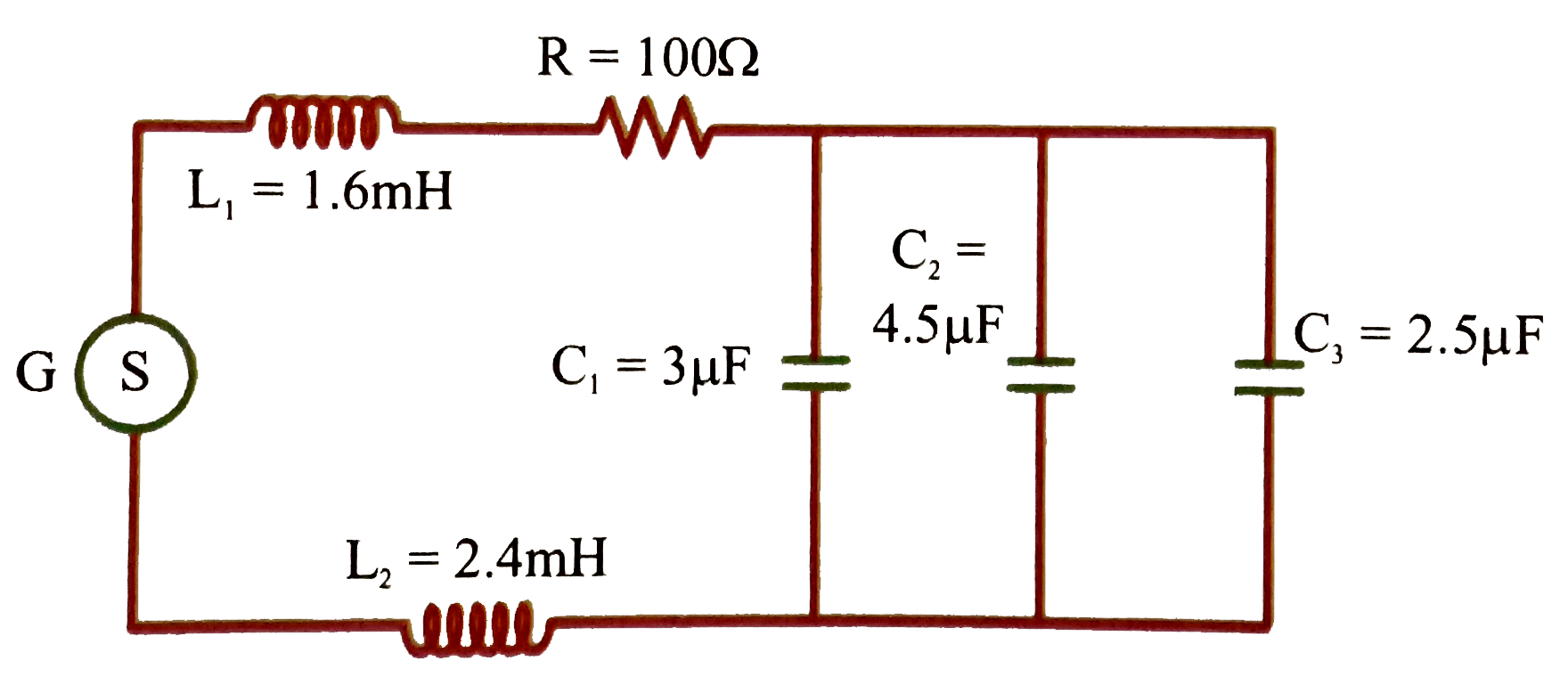
To increase resonant frequency of the circuit, some of the changes in the circuit are carried out. Which changes would certainly result in the increase in resonnatn frequency ?
View SolutionAn ac generator G with an adjustable frequency of oscillation is used in the circuit, as shown.

To increase resonant frequency of the circuit, some of the changes in the circuit are carried out. Which changes would certainly result in the increase in resonant frequency ?
View Solution
