A battery of voltage 12 V sends a current of 400 mA to an appliance. After a long continuous use, the current drops to 320 mA and the appliance does not operate. Find :
the terminal voltage of the battery when the appliance stops operating,
To solve the problem, we need to find the terminal voltage of the battery when the appliance stops operating. Here are the steps to arrive at the solution:
1. Identify Given Values:
- Initial voltage of the battery (V) = 12 V
- Initial current (I) = 400 mA = 0.4 A
- Current after a long use (I1) = 320 mA = 0.32 A
2. Calculate the Resistance of the Appliance:
- Using Ohm's Law, we can find the resistance (R) of the appliance when the current was 400 mA.
- The formula is V=I×R.
- Rearranging gives us R=VI=12 V0.4 A=30Ω.
3. Calculate the Terminal Voltage When Current Drops:
- When the current drops to 320 mA, we can use the same resistance to find the new terminal voltage (V1).
- Using Ohm's Law again, we have:
V1=I1×R
- Substituting the values:
V1=0.32 A×30Ω=9.6 V
4. Conclusion:
- The terminal voltage of the battery when the appliance stops operating is 9.6 V.
- Initial voltage of the battery (V) = 12 V
- Initial current (I) = 400 mA = 0.4 A
- Current after a long use (I1) = 320 mA = 0.32 A
- Using Ohm's Law, we can find the resistance (R) of the appliance when the current was 400 mA.
- The formula is V=I×R.
- Rearranging gives us R=VI=12 V0.4 A=30Ω.
- When the current drops to 320 mA, we can use the same resistance to find the new terminal voltage (V1).
- Using Ohm's Law again, we have:
V1=I1×R
- Substituting the values:
V1=0.32 A×30Ω=9.6 V
- The terminal voltage of the battery when the appliance stops operating is 9.6 V.
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:ICSEChapter:CURRENT ELECTRICITYExercise:EXERCISE-8(A)
Explore 43 Videos
- CURRENT ELECTRICITYBook:ICSEChapter:CURRENT ELECTRICITYExercise:EXERCISE-8(A) ( MULTIPLE CHOICE TYPE)
Explore 2 Videos
- CALORIMETRYBook:ICSEChapter:CALORIMETRYExercise:EXERCISE-11(B) (NUMERICALS)
Explore 15 Videos
- ELECTRO-MAGNETISM Book:ICSEChapter:ELECTRO-MAGNETISM Exercise:EXERCISE-10 (C) NUMERICALS
Explore 1 Video
Similar Questions
A battery of voltage 12 V sends a current of 400 mA to an appliance. After a long continuous use, the current drops to 320 mA and the appliance does not operate. Find :
the voltage drop,
View SolutionA battery of voltage 12 V sends a current of 400 mA to an appliance. After a long continuous use, the current drops to 320 mA and the appliance does not operate. Find :
the internal resistance of the battery.
View Solution
Knowledge Check
A battery of emf 15 V and internal resistance of 4Ω is connected to a resistor. If the current in the circuit is 2A and the circuit is closed. Resistance of the resistor and terminal voltage of the battery will be
A2.5Ω,6VB3.5Ω,6VC2.5Ω,7VD3.5Ω,7VA battery having 12V emf and internal resistance 3Ω is connected to a resistor. If the current in the circuit is 1A, then the resistance of resistor and lost voltage of the battery when circuit is closed will be
A7Ω,7VB8Ω,8VC9Ω,9VD9Ω,10V
A battery of voltage 12 V sends a current of 400 mA to an appliance. After a long continuous use, the current drops to 320 mA and the appliance does not operate. Find :
the resistance of the appliance,
View SolutionA battery of emf 10 V and internal resistance 3Ω is connected to a resistor. If the current in the circuit is 0.5 A, what is the resistance of the resistors ? What is the terminal voltage of the battery when the circuit is closed ?
View SolutionAn ideal voltmeter V is connected to a 2.0Ω resistor and a battery with emf 5.0V and internal resistance 0.5Ω as shown in figure
(a) What is the current in the 2.0Ω resistor?
(b) What is the terminal voltage of the battery?
(c) What is the reading of the voltmeter?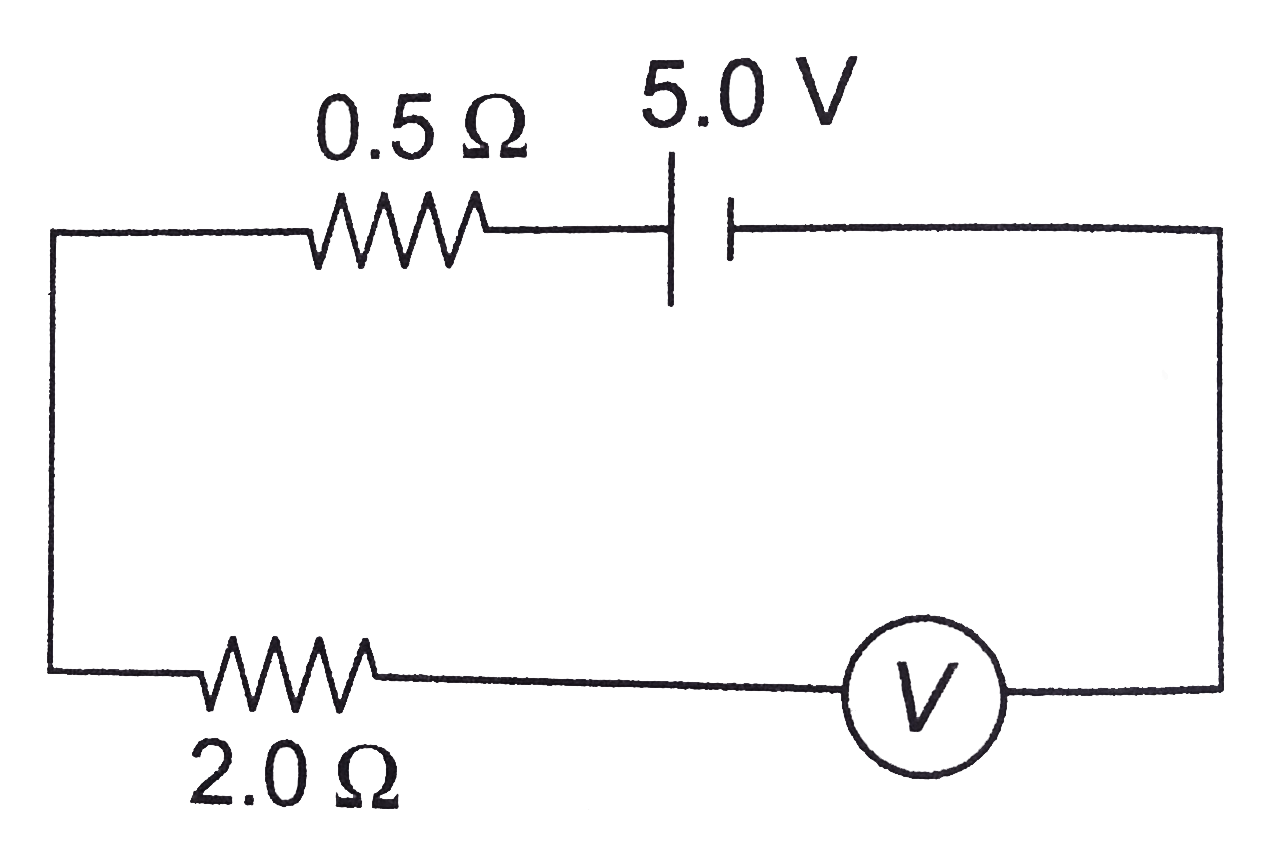
View SolutionA battery of emf 2.0 V and internal resistance 0.50(Ω)supplies a current of 100 mA. Find (a) the potential defference across the terminals of the battary and (b) the thermal energy develop in the battery in 10 s.
View SolutionA car has a fresh storage battery of emt 12V and internal resistance 5.0×10−2Ω. If the starter moter draws a current of 90A, what is the terminal voltage of the battery when the starter is on?
(b) After long use, the internal resistance of the storange battery increase to 500Ω. What maximum current can be drawn from the battery? Assume the emt of the battery to remain unchanged.
(c) If the discharged battery is changed by an external emf source, is the terminal voltage of the battery during changing greater of less than is emf 12V?
View SolutionIn the given circuit the voltage drop across the diode is 0.8 V, if the diode can withstand current upto maximum of 30 mA, then find the maximum voltage of the battery
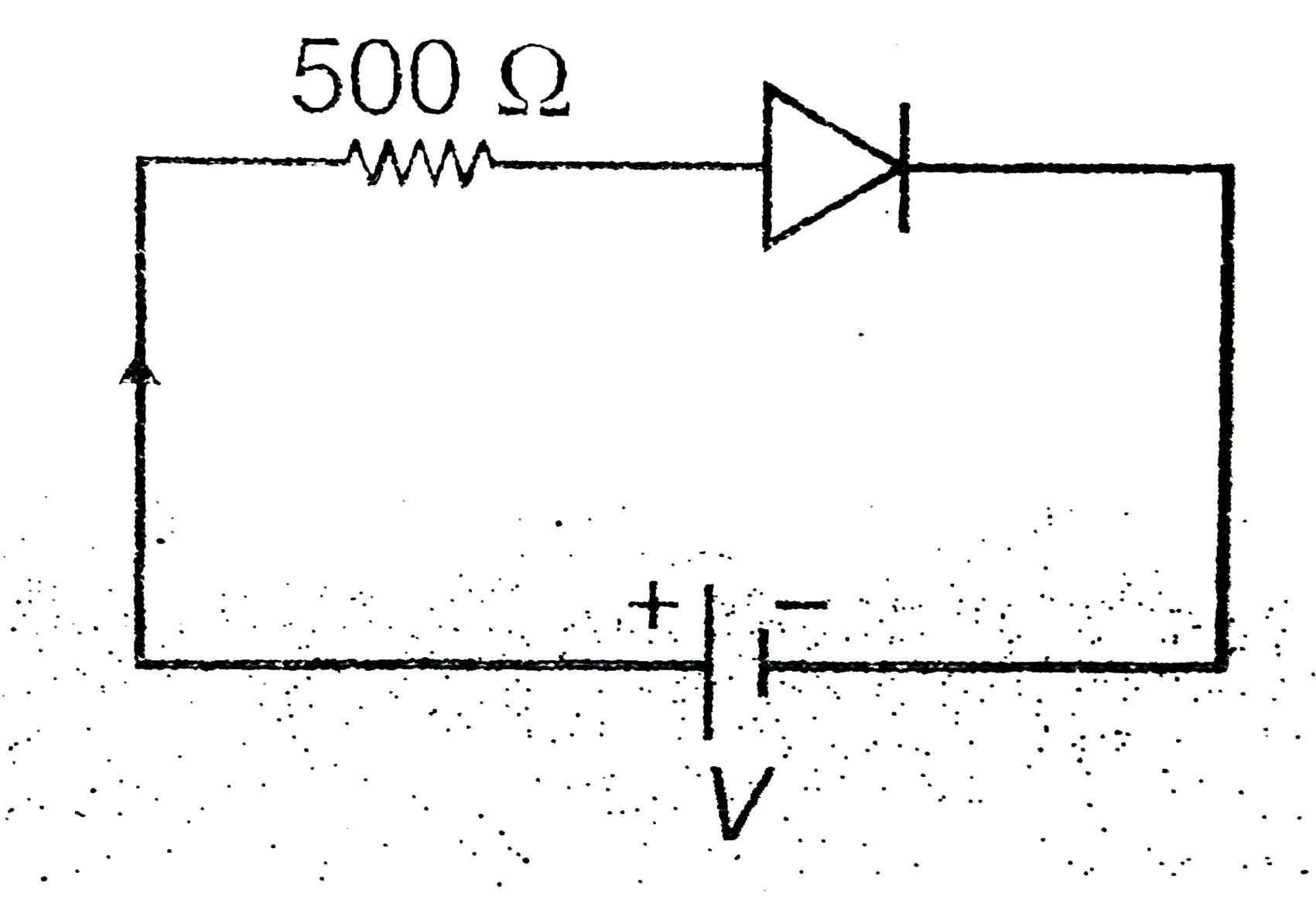
View Solution
