ABC is an equilateral triangle, P is a point in BC such that BP : PC =2 : 1.
Prove that : 9AP2=7AB2
The correct Answer is:9AP2=7AB2
To prove that 9AP2=7AB2 in the given equilateral triangle ABC with point P on side BC such that BP:PC=2:1, we can follow these steps:
Step 1: Define the lengths
Let BP=2x and PC=x. Therefore, the total length of BC is:
BC=BP+PC=2x+x=3x
Step 2: Identify the lengths of the sides of the triangle
Since ABC is an equilateral triangle, all sides are equal. Thus:
AB=AC=BC=3x
Step 3: Draw the altitude from point A to side BC
Let M be the midpoint of BC. Since M is the midpoint, we have:
BM=MC=BC2=3x2=1.5x
Step 4: Determine the lengths of segments
Since P divides BC in the ratio 2:1, we can find the lengths:
MP=BM−BP=1.5x−2x=−0.5x(not applicable, we need to find the correct segment)
Instead, we can find PM:
PM=PC−MC=x−1.5x=−0.5x(this indicates we need to adjust our segments)
We can also find PM as:
PM=1.5x−x=0.5x
Step 5: Apply the Pythagorean theorem in triangles ABM and AMP
For triangle ABM:
AB2=AM2+BM2
Substituting the known values:
(3x)2=AM2+(1.5x)2
9x2=AM2+2.25x2
AM2=9x2−2.25x2=6.75x2
For triangle AMP:
AP2=AM2+MP2
Substituting the known values:
AP2=AM2+(0.5x)2
AP2=6.75x2+0.25x2=7x2
Step 6: Relate AP2 to AB2
Now, substituting back into the equation:
9AP2=9(7x2)=63x2
And for AB2:
AB2=9x2
Thus:
9AP2=7AB2
63x2=7(9x2)=63x2
Conclusion
Therefore, we have proved that:
9AP2=7AB2
Let BP=2x and PC=x. Therefore, the total length of BC is:
BC=BP+PC=2x+x=3x
Since ABC is an equilateral triangle, all sides are equal. Thus:
AB=AC=BC=3x
Let M be the midpoint of BC. Since M is the midpoint, we have:
BM=MC=BC2=3x2=1.5x
Since P divides BC in the ratio 2:1, we can find the lengths:
MP=BM−BP=1.5x−2x=−0.5x(not applicable, we need to find the correct segment)
Instead, we can find PM:
PM=PC−MC=x−1.5x=−0.5x(this indicates we need to adjust our segments)
We can also find PM as:
PM=1.5x−x=0.5x
For triangle ABM:
AB2=AM2+BM2
Substituting the known values:
(3x)2=AM2+(1.5x)2
9x2=AM2+2.25x2
AM2=9x2−2.25x2=6.75x2
AP2=AM2+MP2
Substituting the known values:
AP2=AM2+(0.5x)2
AP2=6.75x2+0.25x2=7x2
Now, substituting back into the equation:
9AP2=9(7x2)=63x2
And for AB2:
AB2=9x2
Thus:
9AP2=7AB2
63x2=7(9x2)=63x2
Therefore, we have proved that:
9AP2=7AB2
Topper's Solved these Questions
Similar Questions
In an equilateral triangle ABC, D is a point on side BC such that BD=13BC. Prove that 9AD2=7AB2.
View SolutionIn the following figure, ABC is an equilateral triangle and P is any point in AC, prove that :
(i) BP>PA
(ii) BP>PC
View SolutionIn the following figure, ABC is an equilateral triangle and P is any point in AC, prove that :
(i) BP>PA
(ii) BP>PC

View SolutionABC is an equilateral triangle where AB = a and P is any point in its plane such that PA = PB + PC. Then PA2+PB2+PC2a2 is
View SolutionIn an equilateral triangle ABC the side BC is trisected at D . Prove that 9 AD2=7 AB2
View SolutionIn an equilateral triangle ABC, BE is perpendicular to side CA. Prove that:
AB2+BC2+CA2=4BE2
View SolutionABC is a triangle in which AB=ACandD is a point on AC such that BC2=AC×CD.Prove that BD=BC.
View SolutionIn the figure, given below, ABCD is a parallelogram. P is a point on BC such that BP : PC = 1: 2. DP produced meets AB produced at Q. Given the area of triangle CPQ=20cm2
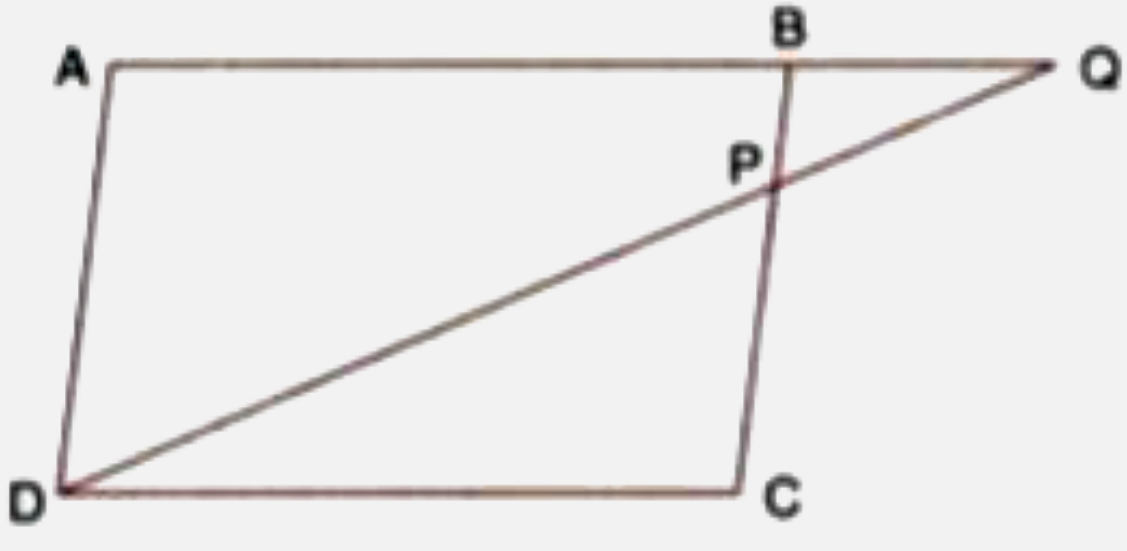
Calculate :
area of triangle CDP.
View SolutionIn the figure, given below, ABCD is a parallelogram. P is a point on BC such that BP : PC = 1: 2. DP produced meets AB produced at Q. Given the area of triangle CPQ=20cm2

Calculate :
area of parallelogram ABCD.
View SolutionIn an isosceles triangle ABC, AB = AC and D is a point on BC produced. Prove that :
AD2=AC2+BD.CD
View Solution