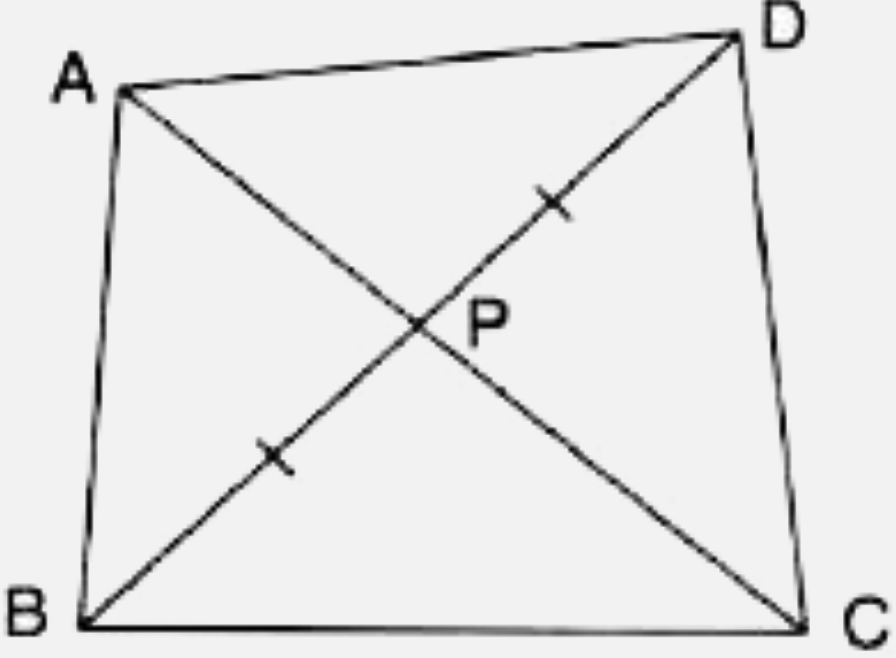
P is the mid-point of diagonal AC of quadrilateral ABCD. Prove that the quadrilaterals ABPD and CBPD are equal in area.
To prove that the areas of quadrilaterals ABPD and CBPD are equal, we will follow these steps:
Step 1: Identify the Given Information
We have a quadrilateral ABCD with diagonal AC. P is the midpoint of diagonal AC, which means:
AP=PC
Step 2: Establish that BP is a Median
Since P is the midpoint of AC, line segment BP acts as a median in triangle ABC. By the property of medians, we know that a median divides a triangle into two triangles of equal area. Therefore, we have:
Area of △ABP=Area of △BPC
Let's denote this area as A1:
A1=Area of △ABP=Area of △BPC
Step 3: Establish that DP is a Median
Similarly, in triangle ADC, since P is the midpoint of AC, line segment DP acts as a median. Thus, we also have:
Area of △ADP=Area of △DPC
Let's denote this area as A2:
A2=Area of △ADP=Area of △DPC
Step 4: Relate Areas to Quadrilaterals
Now, we can express the areas of the quadrilaterals ABPD and CBPD in terms of the areas of the triangles:
- The area of quadrilateral ABPD can be expressed as:
Area of ABPD=Area of △ABP+Area of △ADP=A1+A2
- The area of quadrilateral CBPD can be expressed as:
Area of CBPD=Area of △BPC+Area of △DPC=A1+A2
Step 5: Conclude the Proof
Since both quadrilaterals ABPD and CBPD have the same area:
Area of ABPD=Area of CBPD
Thus, we have proven that the areas of quadrilaterals ABPD and CBPD are equal.
We have a quadrilateral ABCD with diagonal AC. P is the midpoint of diagonal AC, which means:
AP=PC
Since P is the midpoint of AC, line segment BP acts as a median in triangle ABC. By the property of medians, we know that a median divides a triangle into two triangles of equal area. Therefore, we have:
Area of △ABP=Area of △BPC
Let's denote this area as A1:
A1=Area of △ABP=Area of △BPC
Similarly, in triangle ADC, since P is the midpoint of AC, line segment DP acts as a median. Thus, we also have:
Area of △ADP=Area of △DPC
Let's denote this area as A2:
A2=Area of △ADP=Area of △DPC
Now, we can express the areas of the quadrilaterals ABPD and CBPD in terms of the areas of the triangles:
- The area of quadrilateral ABPD can be expressed as:
Area of ABPD=Area of △ABP+Area of △ADP=A1+A2
Area of CBPD=Area of △BPC+Area of △DPC=A1+A2
Since both quadrilaterals ABPD and CBPD have the same area:
Area of ABPD=Area of CBPD
Thus, we have proven that the areas of quadrilaterals ABPD and CBPD are equal.
Topper's Solved these Questions
- CHAPTERWISE REVISION (STAGE 1) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 1) EXERCISE - Circle
6 Videos
- CHAPTERWISE REVISION (STAGE 1) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 1) EXERCISE - Statistics
9 Videos
- CHAPTERWISE REVISION (STAGE 1) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 1) EXERCISE - Rectillinear figures
24 Videos
- CHAPTER REVISION (STAGE 2) BOOK - ICSECHAPTER - CHAPTER REVISION (STAGE 2) EXERCISE - DISTANCE FORMULA
12 Videos
- CHAPTERWISE REVISION (STAGE 3) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 3) EXERCISE - DISTANCE FORMULA
11 Videos
Similar Questions
In trapezium ABCD, side AB is parallel to side DC. Diagonals AC and BD intersect at point P. Prove that triangles APD and BPC are equal in area.
View SolutionO' is any point on diagonal AC of a parallelogram ABCD. Prove that :
area of ΔAOD= area of ΔAOB
View SolutionIf the quadrilateral formed by joining the mid points of the adjacent sides of quadrilateral ABCD is a rectangle, show that the diagonals AC and BD intersect at right angle.
View SolutionIf the diagonals of a quadrilateral bisect each other, then the quadrilateral is a parallelogram.
View SolutionThe diagonals of a quadrilateral ABCD are mutually perpendicular . Prove that the quadrilateral formed by joining the mid-points of its consecutive sides is a reactangle.
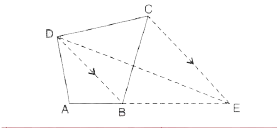
View SolutionIn the following figure, CE is drawn parallel to diagonal DB of the quadrilateral ABCD which meets AB produced ar point E.
Prove that ΔADE and quadrilateral ABCD are equal in area.
View SolutionE, F, G and H are the mid-points of the sides of a parallelogram ABCD. Show that area of quadrilateral EFGH is half of the area of parallelogram ABCD.
View SolutionIn quadrilateral ABCD, diagonal BD is bisected by the diagonal AC. Prove that : ΔABCandΔADC are equal in area.
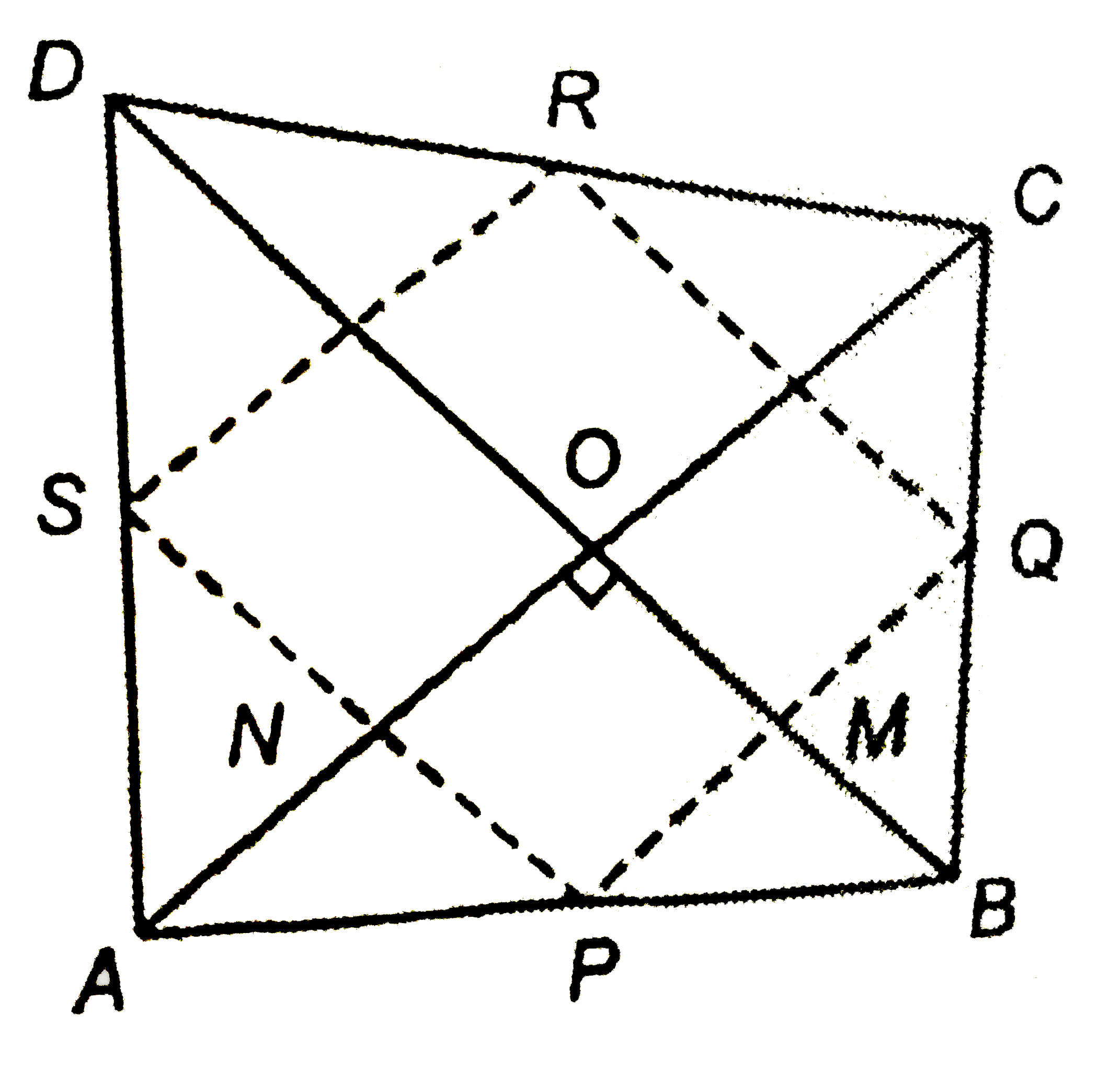
View SolutionP, Q, R and S are respectively the mid-points of sides AB, BC, CD and DA of quadrilateral ABCD in which AC=BD and AC⊥BD. Prove that PQRS is a square.
View SolutionABCD is a rhombus and P, Q, R and S are wthe mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rectangle.
View Solution
