In triangle ABC, D is mid-point of AB and P is any point on BC. If CQ parallel to PD meets AB at Q, prove that: 2× area (ΔBPQ)= area (ΔABC)
Step by step video & image solution for In triangle ABC, D is mid-point of AB and P is any point on BC. If CQ parallel to PD meets AB at Q, prove that: 2 xx " area " (Delta BPQ) = " area "(Delta ABC) by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CHAPTERWISE REVISION (STAGE 1) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 1) EXERCISE - Circle
6 Videos
- CHAPTERWISE REVISION (STAGE 1) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 1) EXERCISE - Statistics
9 Videos
- CHAPTERWISE REVISION (STAGE 1) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 1) EXERCISE - Rectillinear figures
24 Videos
- CHAPTER REVISION (STAGE 2) BOOK - ICSECHAPTER - CHAPTER REVISION (STAGE 2) EXERCISE - DISTANCE FORMULA
12 Videos
- CHAPTERWISE REVISION (STAGE 3) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 3) EXERCISE - DISTANCE FORMULA
11 Videos
Similar Questions
In Δ ABC, D is the mid-point of AB and P is any point on BC. If CQ∣∣PD meets AB and Q (shown in figure), then prove that
ar(ΔBPQ)=12ar(ΔABC).
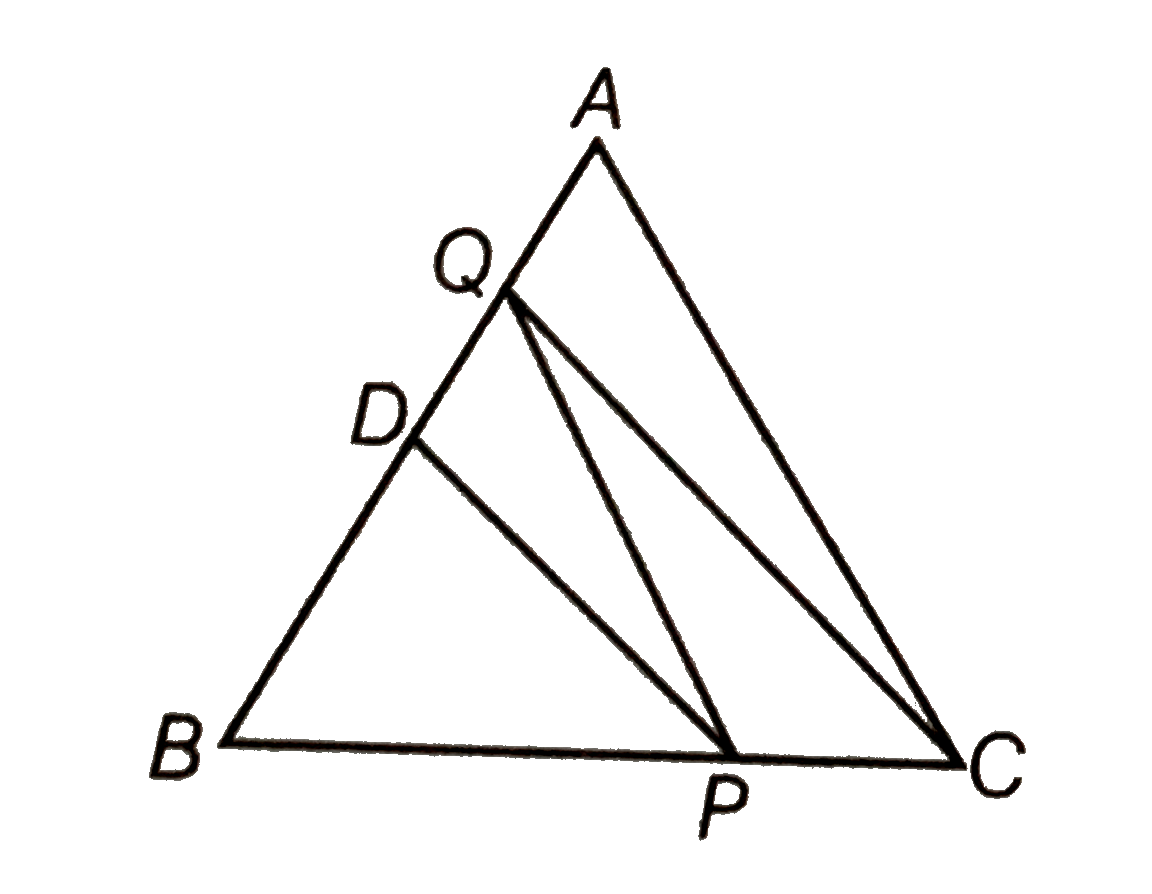
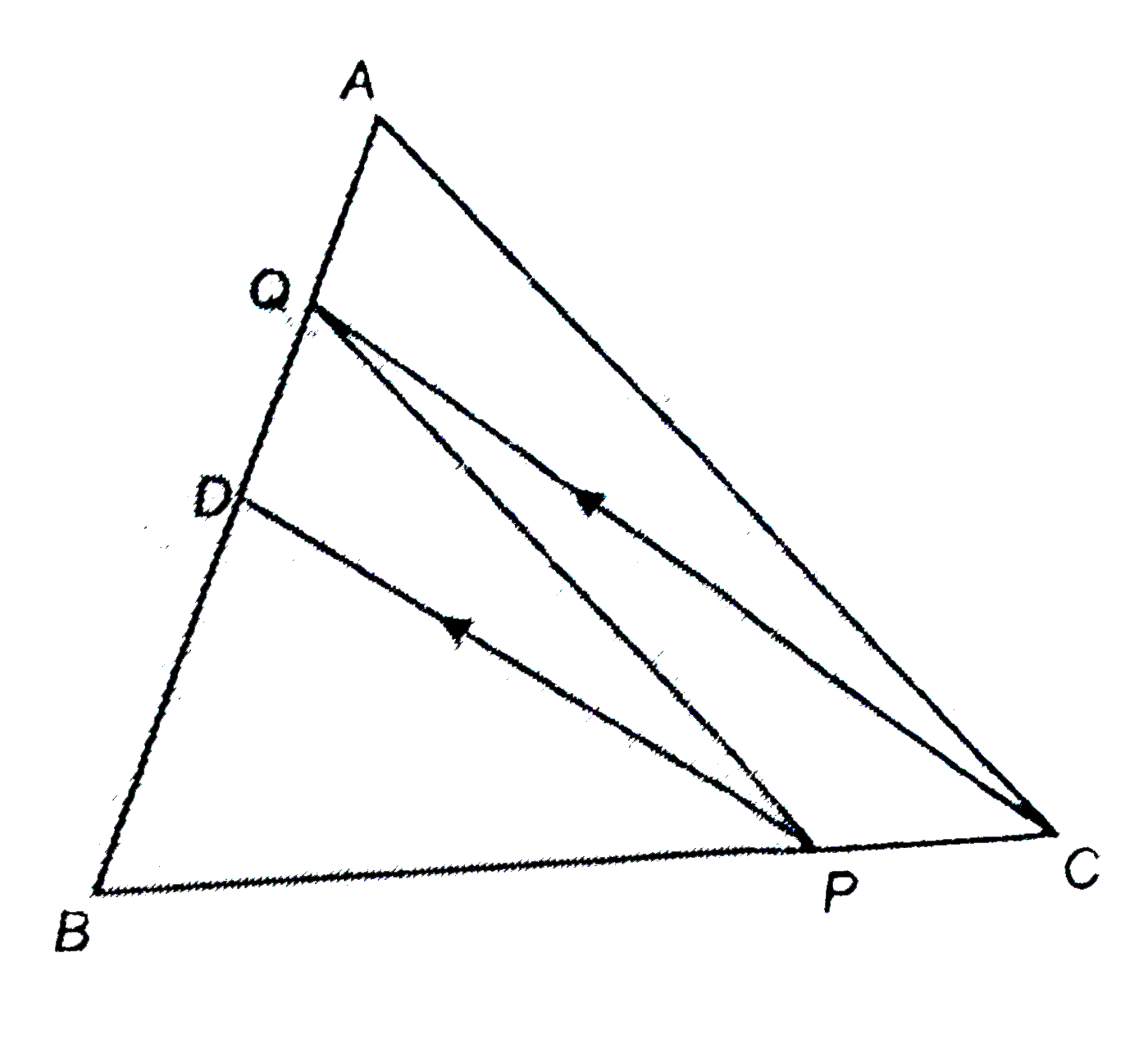
View SolutionIn the adjoining figure, D is the mid-point of side AB of ΔABC and P be any point on side BC. If CQ∣∣PD, then prove that:
area of ΔBPQ=12× area of ΔABC
View SolutionIn ΔABC ,D is a point in side AB and E is a point in AC. If DE is parallel to BC, and BE and CD intersect each other at point 0, prove that:
area (ΔACD)= area (ΔABE)
View SolutionIn ΔABC ,D is a point in side AB and E is a point in AC. If DE is parallel to BC, and BE and CD intersect each other at point 0, prove that:
area (ΔOBD)= area (ΔOCE)
View SolutionD is the mid-point of side AB of the triangle ABC.E is the mid-point of CD and F is the mid-point of AE. Prove that 8× area of (ΔAFD)= area of ΔABC
View SolutionIn triangle ABC,D is the midpoint of AB, E is the midpoint of DB and F is the midpoint of BC. If the area of ΔABC is 96, the area of ΔAEF is
View SolutionIn triangle ABC, AB>AC and D is a point in side BC. Show that : AB>AD.
View SolutionIn triangle ABC, AB>AC and D is a point in side BC. Show that : AB>AD.
View SolutionIn triangle ABC, D is mid-point of AB and CD is perpendiicular to AB. Bisector of ∠ABC meets CD at E and AC at F. Prove that:
F is equidistant from AB and BC.
View SolutionIn triangle ABC, M is mid-point of AB, N is mid-point of AC and D is any point in base BC. Use Intercept Theorem to show that MN bisects AD.
View Solution