Construct a parallelogram ABCD in which AC = 6.5 cm , BD = 7 cm , diagonals AC and BD intersects each other at angle 45∘
To construct the parallelogram ABCD with the given conditions, follow these steps:
1. Draw Line Segment BD:
- Draw a line segment BD that measures 7 cm. Label the endpoints as B and D.
Hint: Use a ruler to measure and draw a straight line of 7 cm.
2. Find the Midpoint O of BD:
- Locate the midpoint O of the line segment BD. This can be done by measuring 3.5 cm from either B or D.
Hint: Since the diagonals bisect each other, O will be the point where diagonals AC and BD intersect.
3. Construct Angle 45°:
- At point O, use a protractor to measure and draw a line at an angle of 45° to the line segment BD.
Hint: Make sure the angle is measured from the line BD to ensure it is accurate.
4. Extend Line AC:
- Extend the line you just drew from point O in both directions. This line represents diagonal AC.
Hint: Label the extended line as AC, ensuring it is straight.
5. Measure Half of AC:
- Since AC = 6.5 cm, calculate half of AC, which is 3.25 cm.
Hint: Half of the diagonal is important for marking points A and C.
6. Mark Points A and C:
- Using a compass, measure 3.25 cm. Place the compass point on O and mark two points on the line AC, one on each side of O. Label these points as A and C.
Hint: Ensure that the total distance between A and C is exactly 6.5 cm.
7. Join Points to Form Parallelogram:
- Now, join points A to B, B to D, D to C, and C to A to complete the parallelogram ABCD.
Hint: Use a ruler to ensure all lines are straight and accurately connected.
Final Result:
You have now constructed the parallelogram ABCD with the diagonals AC = 6.5 cm and BD = 7 cm, intersecting at a 45° angle.
- Draw a line segment BD that measures 7 cm. Label the endpoints as B and D.
- Locate the midpoint O of the line segment BD. This can be done by measuring 3.5 cm from either B or D.
- At point O, use a protractor to measure and draw a line at an angle of 45° to the line segment BD.
- Extend the line you just drew from point O in both directions. This line represents diagonal AC.
- Since AC = 6.5 cm, calculate half of AC, which is 3.25 cm.
- Using a compass, measure 3.25 cm. Place the compass point on O and mark two points on the line AC, one on each side of O. Label these points as A and C.
- Now, join points A to B, B to D, D to C, and C to A to complete the parallelogram ABCD.
You have now constructed the parallelogram ABCD with the diagonals AC = 6.5 cm and BD = 7 cm, intersecting at a 45° angle.
Topper's Solved these Questions
- CHAPTERWISE REVISION (STAGE 3) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 3) EXERCISE - AREA
5 Videos
- CHAPTERWISE REVISION (STAGE 3) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 3) EXERCISE - CIRCLE
7 Videos
- CHAPTERWISE REVISION (STAGE 3) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 3) EXERCISE - RECTILINEAR FIGURES
6 Videos
- CHAPTERWISE REVISION (STAGE 1) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 1) EXERCISE - Graphical solution
10 Videos
- CIRCLEBOOK - ICSECHAPTER - CIRCLEEXERCISE - EXERCISE 17(D)
12 Videos
Similar Questions
Construct a rhombus ABCD in which
AC = 5.6 cm and BD = 6.3 cm
View SolutionFind the area of a parallelogram ABCD in which AB = 8 cm, BC = 15 cm and diagonal AC = 17 cm.
View SolutionConstruct a ΔABC in which AB = 6.3 cm, AC = 4.5 cm and ∠A=45∘.
View SolutionConstructed a parallelogram ABCD, when :
AB=5.8cm, diagonal AC=8.2cm and diagonal BD=6.2cm.
View SolutionConstructed a parallelogram ABCD, when :
AB=6.0cm,AD=5.0cmand∠A=45∘
View SolutionConstruct a parallelogram ABCD in which diagonal AC = 6-3 cm, diagonal BD = 7cm and the acute angles between the diagonals is 45°
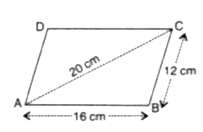
View SolutionIn parallelogram ABCD, AB = 16 cm, BC = 12 cm and diagonal AC = 20 cm. Find the area of the parallelogram.
View SolutionConstructed a parallelogram ABCD, when :
Base BC=5.6cm, diagonal BD=6.5cm and altitude = 3.2cm.
View SolutionConstructed a parallelogram ABCD, when :
AB=4.4cm,AD=6.2cmandAC=4.8cm.
View SolutionConstruct a quadrilateral in which AB=5.4cm,BC=2.5cm,CD=4cm,AC=6.5cmandBD=5cm
View Solution
