In parallelogram ABCD , AB = (3x- 4) cm, BC = ( y- 1) cm , CD = ( y+ 5) cm and AD = (2x+ 5) cm. find the ratio AB : BC.
Find the values of x and y.
The correct Answer is:41:35;x=15andy=36
To solve the problem step by step, we will use the properties of a parallelogram, where opposite sides are equal.
Step 1: Set up the equations based on the properties of the parallelogram.
In parallelogram ABCD:
- AB=CD
- AD=BC
Given:
- AB=3x−4 cm
- BC=y−1 cm
- CD=y+5 cm
- AD=2x+5 cm
From the properties:
1. AB=CD gives us the equation:
3x−4=y+5
2. AD=BC gives us the equation:
2x+5=y−1
Step 2: Simplify the equations.
From Equation 1:
3x−4=y+5
Rearranging gives:
3x−y−9=0(Equation 3)
From Equation 2:
2x+5=y−1
Rearranging gives:
2x−y+6=0(Equation 4)
Step 3: Solve the system of equations.
We have two equations:
1. 3x−y−9=0 (Equation 3)
2. 2x−y+6=0 (Equation 4)
To eliminate y, we can subtract Equation 4 from Equation 3:
(3x−y−9)−(2x−y+6)=0
This simplifies to:
3x−y−9−2x+y−6=0
Combining like terms gives:
x−15=0
Thus, we find:
x=15
Step 4: Substitute x back into one of the equations to find y.
Using Equation 3:
3(15)−y−9=0
Calculating gives:
45−y−9=0
This simplifies to:
36−y=0⇒y=36
Step 5: Find the ratio AB:BC.
Now we can find the ratio:
AB=3x−4=3(15)−4=45−4=41 cm
BC=y−1=36−1=35 cm
Thus, the ratio AB:BC is:
ABBC=4135
Final Answers:
- Values: x=15, y=36
- Ratio AB:BC=41:35
---
- AB=CD
- AD=BC
- AB=3x−4 cm
- BC=y−1 cm
- CD=y+5 cm
- AD=2x+5 cm
1. AB=CD gives us the equation:
3x−4=y+5
2. AD=BC gives us the equation:
2x+5=y−1
3x−4=y+5
Rearranging gives:
3x−y−9=0(Equation 3)
2x+5=y−1
Rearranging gives:
2x−y+6=0(Equation 4)
1. 3x−y−9=0 (Equation 3)
2. 2x−y+6=0 (Equation 4)
(3x−y−9)−(2x−y+6)=0
This simplifies to:
3x−y−9−2x+y−6=0
Combining like terms gives:
x−15=0
Thus, we find:
x=15
3(15)−y−9=0
Calculating gives:
45−y−9=0
This simplifies to:
36−y=0⇒y=36
AB=3x−4=3(15)−4=45−4=41 cm
BC=y−1=36−1=35 cm
Thus, the ratio AB:BC is:
ABBC=4135
- Values: x=15, y=36
- Ratio AB:BC=41:35
Topper's Solved these Questions
- CHAPTERWISE REVISION (STAGE 3) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 3) EXERCISE - CONSTRUCTIONS OF POLYGONS
4 Videos
- CHAPTERWISE REVISION (STAGE 3) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 3) EXERCISE - AREA
5 Videos
- CHAPTERWISE REVISION (STAGE 3) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 3) EXERCISE - PYTHAGORAS THEOREM
5 Videos
- CHAPTERWISE REVISION (STAGE 1) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 1) EXERCISE - Graphical solution
10 Videos
- CIRCLEBOOK - ICSECHAPTER - CIRCLEEXERCISE - EXERCISE 17(D)
12 Videos
Similar Questions
The perimeter of a parallelogram ABCD = 40 cm , AB = 3x cm, BC = 2x cm and CD = 2( y+1) cm . Find the values of x and y.
View Solution∆ABC ~ ∆DEF. If AB = 4 cm, BC = 3.5 cm, CA = 2.5 cm and DF = 7.5 cm, find the perimeter of ∆DEF
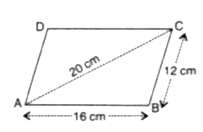
View SolutionIn parallelogram ABCD, AB = 16 cm, BC = 12 cm and diagonal AC = 20 cm. Find the area of the parallelogram.
View SolutionIn the given figure, AB||CDandBC||AD. Find the values of x, y and z

View SolutionConstruct a quadrilateral in which AB=5.4cm,BC=2.5cm,CD=4cm,AC=6.5cmandBD=5cm
View SolutionIn ΔABC,∠ABC=∠DAC,AB=8cm,AC=4cmandAD=5cm.

Find BC and CD.
View SolutionIn the given figure, in ΔABC,DE∣∣BC so that AD= (4x - 3) cm, AE= ( 8x-7) cm, BD= (3x-1) cm and CE= (5x-3) cm . Find the value of x.
View SolutionConstruct a quadrilateral ABCD in which AB=4.4cm,BC=4cm,CD=6.4cm,DA=2.8cmandBD=6.6cm
View SolutionA park is in the shape of quadrilateral ABCD in which AB = 9 cm, BC = 12 cm, CD = 5 cm, AD = 8 cm and ∠C=90∘. Find the area of the park.
View SolutionIn the given figure, ΔABC is similar to ΔDEF,AB=(x−0.5) cm, AC=1.5xcm,DE=9cm,andDF=3xcm. Find the lengths of AB and DF.
View Solution
