ABCD is an isosceles trapezium with AB parallel to DC, AD = BC = 12 cm, ∠A=60∘andDC=16cm. Taking √3=1.732, find
length of side AB.
The correct Answer is:28cm
To find the length of side AB in the isosceles trapezium ABCD, we will follow these steps:
Step 1: Understand the trapezium configuration
We have an isosceles trapezium ABCD where AB is parallel to DC. Given:
- AD=BC=12cm
- DC=16cm
- ∠A=60∘
Step 2: Draw perpendiculars from points D and C to line AB
To find the length of AB, we can drop perpendiculars from points D and C to line AB. Let's denote the foot of the perpendicular from D as point P and from C as point Q. This creates two right triangles, ADP and BCQ.
Step 3: Identify the height and base
In triangles ADP and BCQ:
- The height (DP and CQ) is equal to the length of AD (or BC), which is 12cm.
- We need to find the base lengths AP and BQ.
Step 4: Use trigonometric ratios
Using the cosine function in triangle ADP:
cos(60∘)=APAD
Given AD=12cm and cos(60∘)=12:
12=AP12
Multiplying both sides by 12 gives:
AP=6cm
Step 5: Find BQ using the same reasoning
Since ABCD is an isosceles trapezium, the lengths AP and BQ are equal:
BQ=AP=6cm
Step 6: Calculate the length of AB
Now, we can find the length of AB:
AB=DC+AP+BQ
Substituting the known values:
AB=16+6+6=28cm
Final Answer
The length of side AB is 28cm.
---
We have an isosceles trapezium ABCD where AB is parallel to DC. Given:
- AD=BC=12cm
- DC=16cm
- ∠A=60∘
To find the length of AB, we can drop perpendiculars from points D and C to line AB. Let's denote the foot of the perpendicular from D as point P and from C as point Q. This creates two right triangles, ADP and BCQ.
In triangles ADP and BCQ:
- The height (DP and CQ) is equal to the length of AD (or BC), which is 12cm.
- We need to find the base lengths AP and BQ.
Using the cosine function in triangle ADP:
cos(60∘)=APAD
Given AD=12cm and cos(60∘)=12:
12=AP12
Multiplying both sides by 12 gives:
AP=6cm
Since ABCD is an isosceles trapezium, the lengths AP and BQ are equal:
BQ=AP=6cm
Now, we can find the length of AB:
AB=DC+AP+BQ
Substituting the known values:
AB=16+6+6=28cm
The length of side AB is 28cm.
Topper's Solved these Questions
- CHAPTERWISE REVISION (STAGE 3) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 3) EXERCISE - CO-ORDINATE GEOMETRY
6 Videos
- CHAPTERWISE REVISION (STAGE 3) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 3) EXERCISE - GRAPHICAL SOLUTION
3 Videos
- CHAPTERWISE REVISION (STAGE 3) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 3) EXERCISE - SOLIDS
6 Videos
- CHAPTERWISE REVISION (STAGE 1) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 1) EXERCISE - Graphical solution
10 Videos
- CIRCLEBOOK - ICSECHAPTER - CIRCLEEXERCISE - EXERCISE 17(D)
12 Videos
Similar Questions
Knowledge Check
ABCD is a trapezium with AB parallel to DC. Then the triangle similar to ΔAOB is:
 AΔADBBΔACBCΔCODDΔCOB
AΔADBBΔACBCΔCODDΔCOB
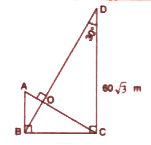
In the given figure, AB⊥BC,DC⊥BC,BD⊥AC,∠D=30∘andDC=60√3 m. Find the length of AB.
View SolutionIn trapezium ABCD, as shown, AB // DC, AD = DC = BC = 20 cm and ∠A=60∘. Find:
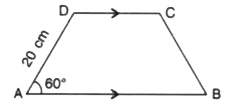
(i) length of AB
View SolutionFind the area of the trapezium ABCD in which AB//DC, AB = 18 cm, ∠B=∠C=90∘, CD = 12 cm and AD = 10 cm.
View SolutionCalculate the area of the quadrilateral ABCD in which
AB =BD =AD = 10 cm , ∠BCD=90∘andCD=8 cm . (Take √3=1.732).

View SolutionConstruct a parallelogram ABCD with ∠A=60∘ and adjacent sides AB = 4 cm and AD = 7 cm.
View SolutionIn trapezium ABCD, as shown, AB // DC, AD = DC = BC = 20 cm and ∠A=60∘. Find:
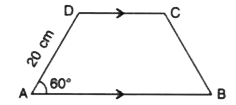
(ii) distance between AB and DC.
View SolutionIn trapezium ABCD, as shown, AB||DC, AD = DC = BC = 20 cm and ∠A=60∘ Find :
 (i) length of AB
(i) length of AB
(ii) distance between AB and DC
View Solution
