If , prove that : .
To prove that ax=by given the equation (a2+b2)(x2+y2)=(ax+by)2, we can follow these steps:
Step 1: Start with the given equation
We start with the equation:
(a2+b2)(x2+y2)=(ax+by)2
Step 2: Expand both sides
Expand the left-hand side:
a2x2+a2y2+b2x2+b2y2
And expand the right-hand side:
(ax+by)2=a2x2+2axy+b2y2
Step 3: Set the expanded forms equal to each other
Now, we set the expanded forms equal to each other:
a2x2+a2y2+b2x2+b2y2=a2x2+2axy+b2y2
Step 4: Rearrange the equation
Subtract a2x2 and b2y2 from both sides:
a2y2+b2x2−2axy=0
Step 5: Rearrange further
Rearranging gives us:
a2y2+b2x2=2axy
Step 6: Recognize the form of a perfect square
Notice that the left-hand side can be rewritten as:
(ay)2+(bx)2−2(ay)(bx)=0
This is the form of a perfect square:
(ay−bx)2=0
Step 7: Solve the equation
From (ay−bx)2=0, we conclude:
ay−bx=0⟹ay=bx
Step 8: Rearranging gives the desired ratio
Dividing both sides by xy gives:
ax=by
Conclusion
Thus, we have proved that:
ax=by
We start with the equation:
(a2+b2)(x2+y2)=(ax+by)2
Expand the left-hand side:
a2x2+a2y2+b2x2+b2y2
And expand the right-hand side:
(ax+by)2=a2x2+2axy+b2y2
Now, we set the expanded forms equal to each other:
a2x2+a2y2+b2x2+b2y2=a2x2+2axy+b2y2
Subtract a2x2 and b2y2 from both sides:
a2y2+b2x2−2axy=0
Rearranging gives us:
a2y2+b2x2=2axy
Notice that the left-hand side can be rewritten as:
(ay)2+(bx)2−2(ay)(bx)=0
This is the form of a perfect square:
(ay−bx)2=0
From (ay−bx)2=0, we conclude:
ay−bx=0⟹ay=bx
Dividing both sides by xy gives:
ax=by
Thus, we have proved that:
ax=by
Topper's Solved these Questions
- RATIO AND PROPORTION (INCLUDING PROPERTIES AND USES)BOOK - ICSECHAPTER - RATIO AND PROPORTION (INCLUDING PROPERTIES AND USES)EXERCISE - Exercise 7(D)
27 Videos
- RATIO AND PROPORTION (INCLUDING PROPERTIES AND USES)BOOK - ICSECHAPTER - RATIO AND PROPORTION (INCLUDING PROPERTIES AND USES)EXERCISE - QUESTIONS
30 Videos
- RATIO AND PROPORTION (INCLUDING PROPERTIES AND USES)BOOK - ICSECHAPTER - RATIO AND PROPORTION (INCLUDING PROPERTIES AND USES)EXERCISE - Exercise 7(B)
17 Videos
- RATIO AND PROPORTIONBOOK - ICSECHAPTER - RATIO AND PROPORTIONEXERCISE - MULTIPLE CHOICE QUESTION
61 Videos
- REFLECTION BOOK - ICSECHAPTER - REFLECTION EXERCISE - QUESTION
1 Videos
Similar Questions
If xa=yb=zcandy2=xz, prove that b=2aca+c
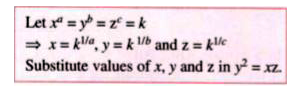
View SolutionIf x+iy=a+iba−ib,prove that x2+y2=1.
View Solutionax−by=a2+b2x+y=2a
View SolutionFactorise : (iv) ax2+b2y−ab2−x2y
View Solution(prove that) If the polar of the points on the circle
x2+y2=a2 with respect to the circle
x2+y2=b2 touches the circle x2+y2=c2
then prove that a, b, c, are in Geometrical
progression.
View SolutionIf y=ax+bx2+c, prove that (2xy1+y)y3=3(xy2+y1)y2.
View SolutionIf ax2+by2=1 cut a'x2+b'y2=1 orthogonally, then
View SolutionIf y2=a2cos2x+b2sin2x then prove that d2ydx2+y=a2b2y3
View SolutionIf x+iy=a+iba−ib prove that x2+y2=1
View SolutionThe foci of hyperbola xy=((a^2 + b^2)/(4))aregivenby(A)x = y = +- ((a^2 + b^2)/(4a))(B)x = y = +- ((a^2 + b^2)/(4b))(C)x = y = +- ((a^2 + b^2)/(2a))(D)x = y = +- ((a^2 + b^2)/(2b))
View Solution
