Find :
tan53∘38'
To find the value of tan53∘38′, we will follow these steps:
Step 1: Convert minutes to degrees
We know that:
- 1 degree = 60 minutes
- Therefore, 1 minute = 160 degrees.
Given 38′ (38 minutes), we convert it to degrees:
38′=3860 degrees
Step 2: Calculate the decimal value of minutes in degrees
Now, we calculate 3860:
3860=0.6333… (approximately 0.63)
Step 3: Add the converted minutes to the degrees
Now, we add this value to the degrees:
53∘38′=53∘+0.6333…∘=53.6333…∘
Step 4: Calculate the tangent of the angle
Now we need to find tan(53.6333…∘). Using a calculator:
tan(53.6333…∘)≈1.35
Final Answer
Thus, the value of tan53∘38′ is approximately:
tan53∘38′≈1.35
---
We know that:
- 1 degree = 60 minutes
- Therefore, 1 minute = 160 degrees.
38′=3860 degrees
Now, we calculate 3860:
3860=0.6333… (approximately 0.63)
Now, we add this value to the degrees:
53∘38′=53∘+0.6333…∘=53.6333…∘
Now we need to find tan(53.6333…∘). Using a calculator:
tan(53.6333…∘)≈1.35
Thus, the value of tan53∘38′ is approximately:
tan53∘38′≈1.35
Topper's Solved these Questions
Similar Questions
y−x curve at an instant for a wave travelling along x−axis on a string is shown. Slope at the point A on the curve, as shown, is tan53∘.
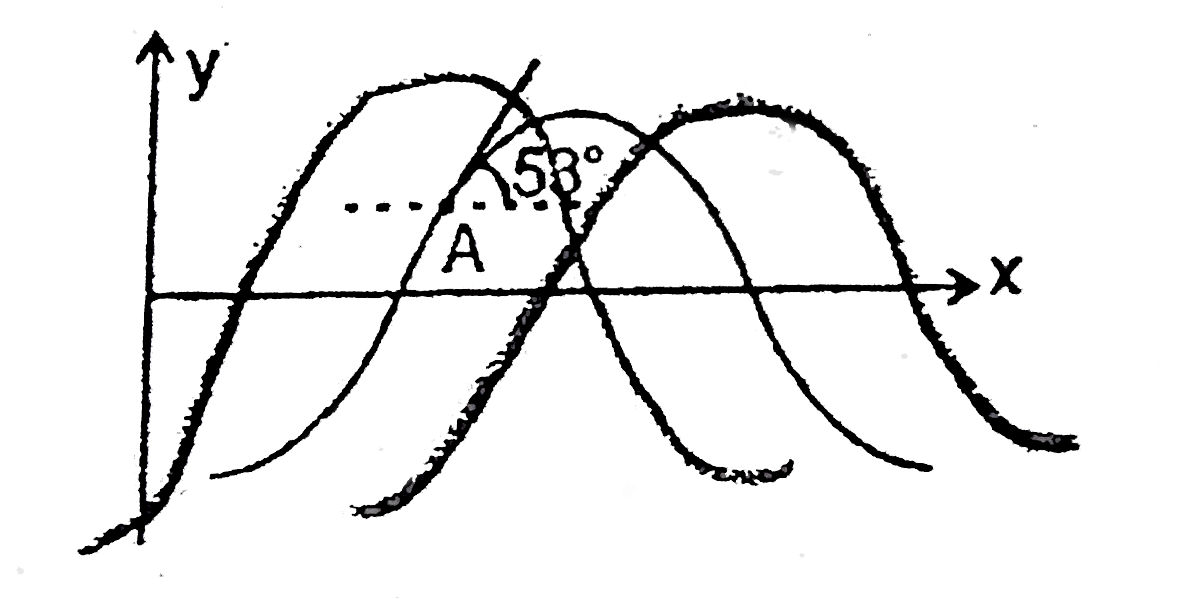
View Solutiony−x curve at an instant for a wave travelling along x−axis on a string is shown. Slope at the point A on the curve, as shown, is tan53∘.
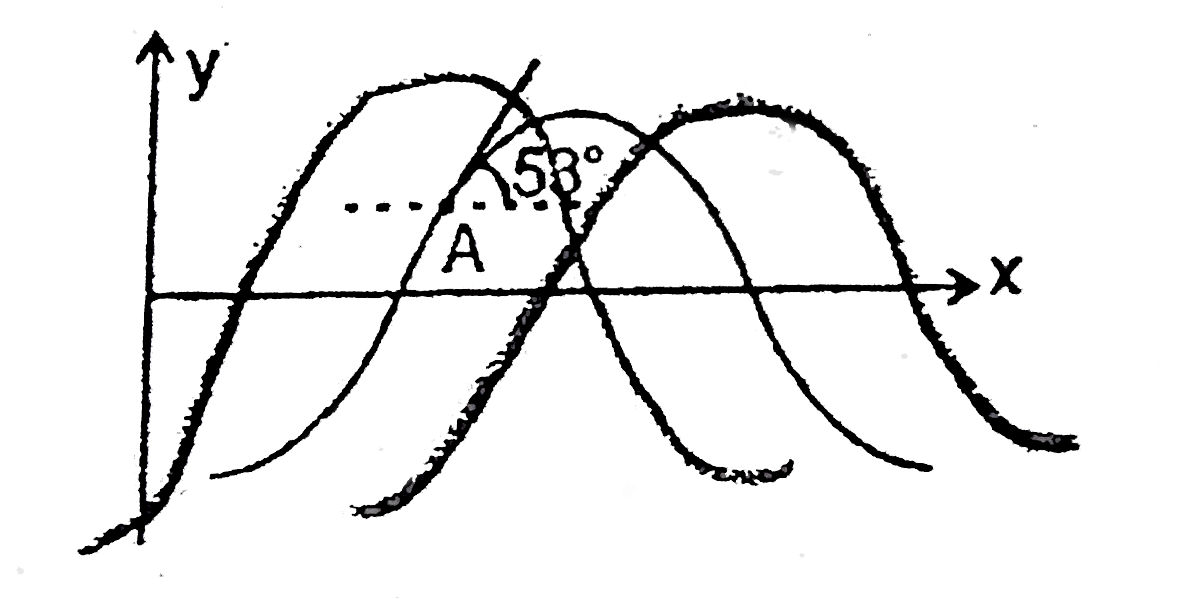
View Solution6cosθ+8sinθ=9, when tan53∘8′=43 and cos25∘50′=910
View SolutionFind the complement of each of the following angles
53∘24'32''
View SolutionEvaluate: 2tan53∘cot37∘−cot80∘tan10∘
View SolutionEvaluate: 2tan53∘cot37∘−cot80∘tan10∘
View SolutionEvaluate without using trigonometric tables :
tan20∘tan40∘tan50∘tan70∘
View SolutionGiven that tanA=15. find the values of tan 2 A, tan 4A and tan(45∘−4A).
View SolutionEvaluate without using trigonometric tables :
tan20.tan40∘tan50∘tan70∘
View SolutionFind (in each case, given below) the value of x, if :
tanx=tan60∘−tan30∘1+tan60∘tan30∘
View Solution
