In the figure, EF || AC, BC = 10 cm, AB = 13 cm and EC = 2 cm, find AF
The correct Answer is:2.6 cm
To solve the problem step by step, we will use the information given and apply Thales' theorem.
Step 1: Understand the Given Information
We have a figure where EF is parallel to AC. The lengths given are:
- BC = 10 cm
- AB = 13 cm
- EC = 2 cm
We need to find the length of AF.
Step 2: Calculate BE
Since EF is parallel to AC, we can find the length of BE using the relation:
BE=BC−EC
Substituting the values:
BE=10cm−2cm=8cm
Step 3: Set Up the Variables
Let:
- AF = x cm
- BF = AB - AF = 13 cm - x cm
Step 4: Apply Thales' Theorem
According to Thales' theorem, the ratios of the segments are equal:
BFAF=BEEC
Substituting the known values:
13−xx=82
This simplifies to:
13−xx=4
Step 5: Cross-Multiply to Solve for x
Cross-multiplying gives:
13−x=4x
Now, rearranging the equation:
13=4x+x
13=5x
Step 6: Solve for x
Dividing both sides by 5:
x=135
Calculating this gives:
x=2.6cm
Step 7: Conclusion
Thus, the length of AF is:
AF=2.6cm
We have a figure where EF is parallel to AC. The lengths given are:
- BC = 10 cm
- AB = 13 cm
- EC = 2 cm
Since EF is parallel to AC, we can find the length of BE using the relation:
BE=BC−EC
Substituting the values:
BE=10cm−2cm=8cm
Let:
- AF = x cm
- BF = AB - AF = 13 cm - x cm
According to Thales' theorem, the ratios of the segments are equal:
BFAF=BEEC
Substituting the known values:
13−xx=82
This simplifies to:
13−xx=4
Cross-multiplying gives:
13−x=4x
Now, rearranging the equation:
13=4x+x
13=5x
Dividing both sides by 5:
x=135
Calculating this gives:
x=2.6cm
Thus, the length of AF is:
AF=2.6cm
Topper's Solved these Questions
- MEASURES OF CENTRAL TENDENCY (MEAN, MEDIAN, QUARTILES AND MODE)BOOK - ICSECHAPTER - MEASURES OF CENTRAL TENDENCY (MEAN, MEDIAN, QUARTILES AND MODE)EXERCISE - EXERCISE 24 (D)
8 Videos
- MATRICESBOOK - ICSECHAPTER - MATRICESEXERCISE - Exercise 9D
25 Videos
- MIXED PRACTICE BOOK - ICSECHAPTER - MIXED PRACTICE EXERCISE - SET B
52 Videos
Similar Questions
In the given figure, if DE || BC, AE = 8 cm, EC = 2 cm and BC = 6 cm, then find DE
View SolutionIn the adjoining figure, AB=8cm,DM=6cmandBC=6cm. Find the length of DN

View SolutionIn the given figure, AB∣∣CD,AB=7cm,BD=25cmandCD=17cm, find the length of side BC.

View SolutionIn the given figure, DE//BC,AE=15cm,EC=9cm,NC=6cmandBN=24cm.
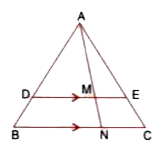
Find lengths of ME and DM.
View SolutionIn the given figure, ∠B=60∘,AB=16 cm and BC=23 cm.

Calculate:
(ii) AC.
View SolutionIf P and Q are points on the sides AB and AC respeactively of △ABC, if PQ||BC,l AP= 2 cm , AB = 6 cm and AC= 9 cm find AQ.
View SolutionIn the given figure, ΔABC and ΔAMP are right angled at B and M respectively.
Given AC=10cm,AP=15cmandPM=12cm.
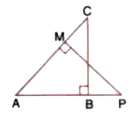
Find : AB and BC.
View SolutionIn Fig. 2, ΔAHK is similar to ΔABC. If AK=10cm,BC=3.5cm and HK=7cm, find AC. -
View SolutionIn parallelogram ABCD, AB = 16 cm, BC = 12 cm and diagonal AC = 20 cm. Find the area of the parallelogram.
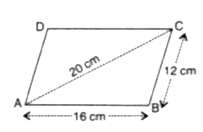
View SolutionIn triangle ABC, AB = AC = 15 cm and BC = 18 cm, find cos ∠ABC
View Solution
