In the given figure, QA ⊥ AB and PB ⊥ AB. If AO = 20 cm, BO = 12 cm, PB = 18 cm, find AQ
The correct Answer is:30 cm
To solve the problem, we will follow these steps:
1. Identify the triangles: We have two triangles, △OAQ and △OBP. Since QA and PB are both perpendicular to AB, we can use the properties of similar triangles.
2. Establish similarity: Since QA⊥AB and PB⊥AB, we know that ∠OAQ=90∘ and ∠OBP=90∘. Additionally, ∠AOQ and ∠BOP are vertically opposite angles, which means they are equal. Therefore, by the Angle-Angle (AA) similarity criterion, △OAQ∼△OBP.
3. Set up the proportion: From the similarity of the triangles, we can set up the following proportion based on corresponding sides:
AOBO=AQPB
Substituting the known values:
20cm12cm=AQ18cm
4. Cross-multiply to solve for AQ:
20⋅18=12⋅AQ
This simplifies to:
360=12⋅AQ
5. Isolate AQ:
AQ=36012
Simplifying this gives:
AQ=30cm
Thus, the length of AQ is 30cm.
AOBO=AQPB
Substituting the known values:
20cm12cm=AQ18cm
20⋅18=12⋅AQ
This simplifies to:
360=12⋅AQ
AQ=36012
Simplifying this gives:
AQ=30cm
Topper's Solved these Questions
- MEASURES OF CENTRAL TENDENCY (MEAN, MEDIAN, QUARTILES AND MODE)BOOK - ICSECHAPTER - MEASURES OF CENTRAL TENDENCY (MEAN, MEDIAN, QUARTILES AND MODE)EXERCISE - EXERCISE 24 (D)
8 Videos
- MATRICESBOOK - ICSECHAPTER - MATRICESEXERCISE - Exercise 9D
25 Videos
- MIXED PRACTICE BOOK - ICSECHAPTER - MIXED PRACTICE EXERCISE - SET B
52 Videos
Similar Questions
In the given figure, AP = 8 cm, BP = 22 cm, AQ = 12 cm and QC = 8 cm

If PQ = 14 cm, find BC.
View SolutionIn the given figure, AB and DE are perpendiculars to BC. If AB = 9 cm, DE = 3 cm and AC = 24 cm, calculate AD.

View SolutionIn the figure given below, AB // EF // CD. If AB = 22.5 cm, EP = 7.5 cm, PC = 15 cm and DC = 27 cm.
Calculate :
AC

View SolutionIn the figure given below, AB // EF // CD. If AB = 22.5 cm, EP = 7.5 cm, PC = 15 cm and DC = 27 cm.
Calculate :
EF
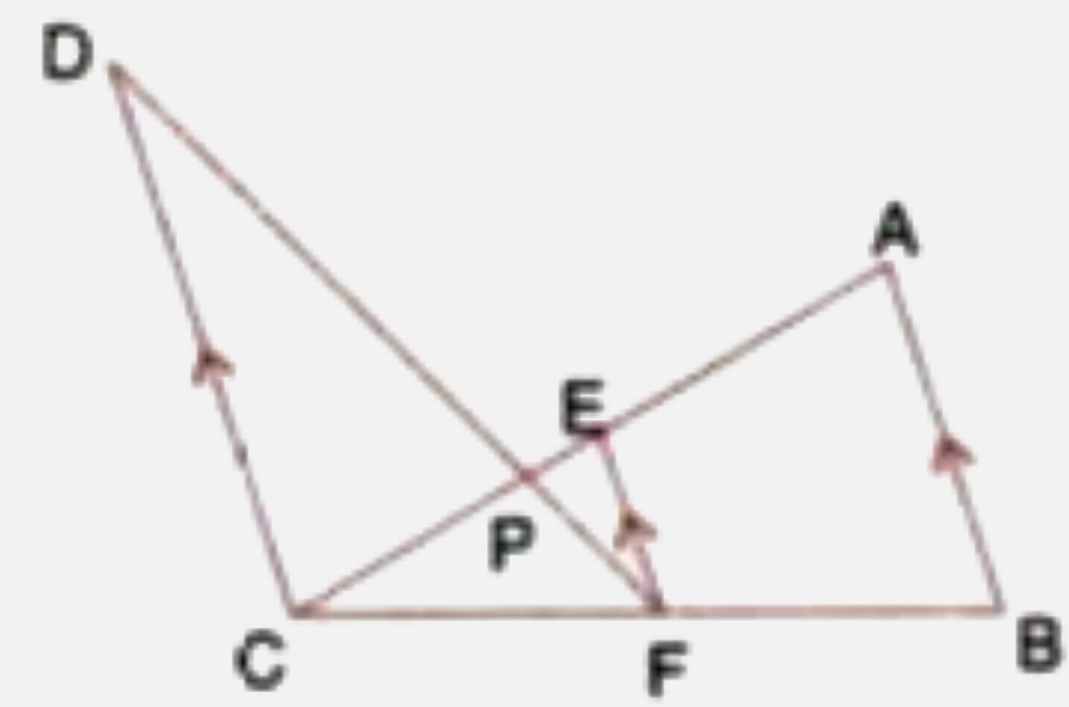
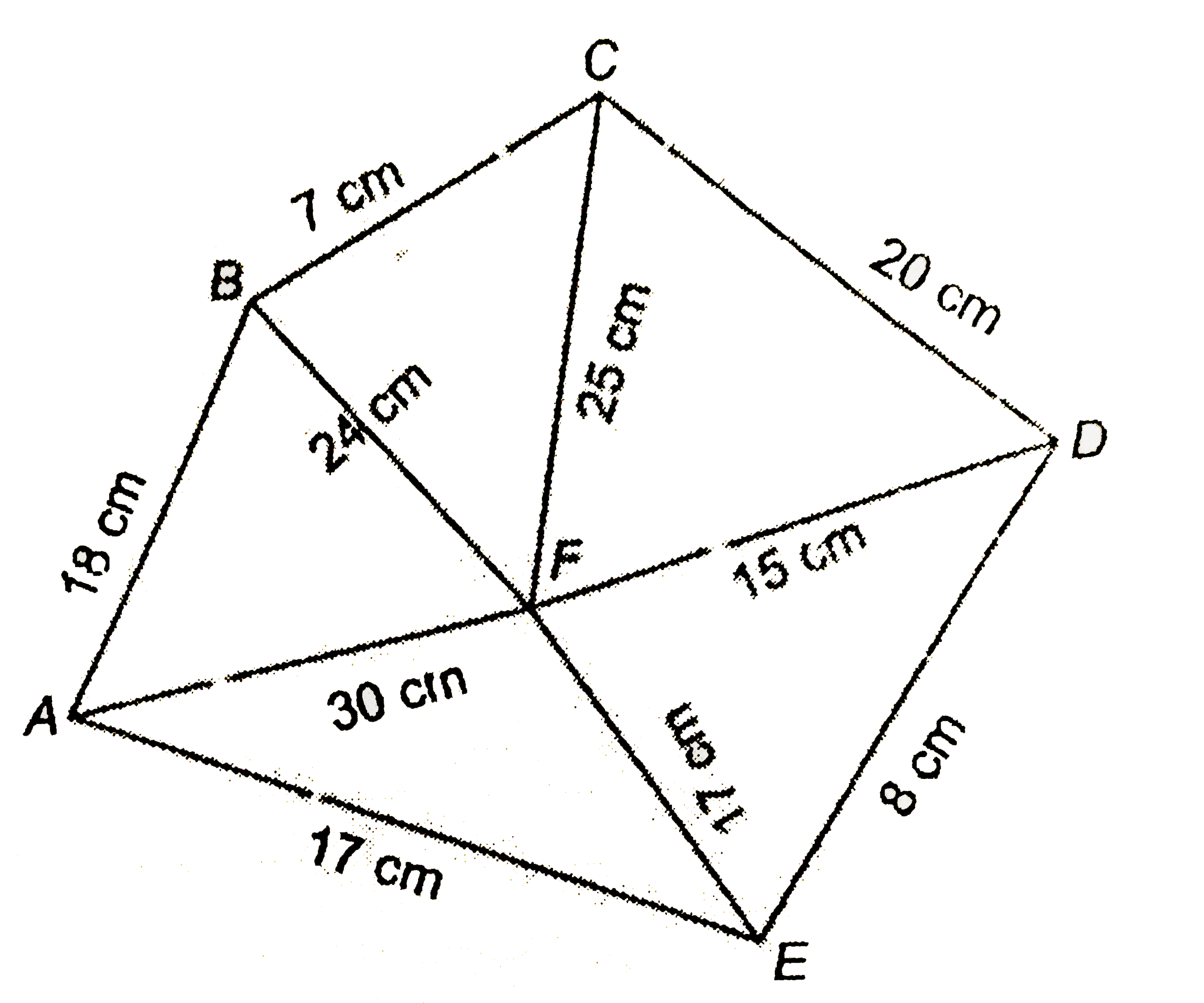
View SolutionFind the area of the given figure
Given AB = 18 cm, BC = 7 cm, CD = 20 cm, DE = 8 cm, EA = 17 cm, AF = 30 cm, BF = 24 cm, CF = 25 cm, FD = 15 cm, EF = 17 cm.
View SolutionIn the given figure, AB and DE are perpendiculars to BC
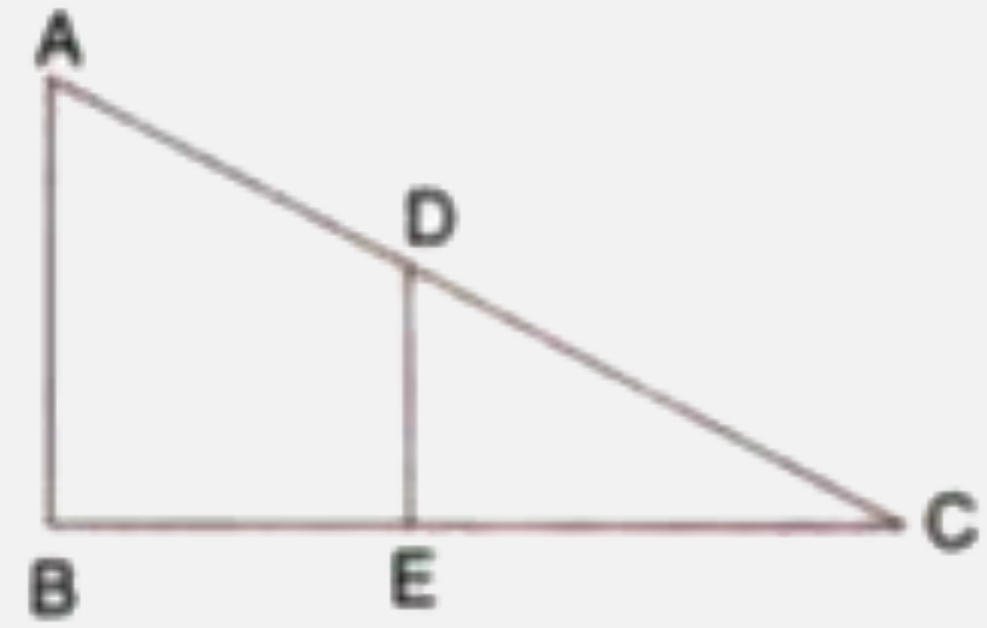
If AB = 6 cm, DE = 4 cm and AC = 15 cm. Calculate CD.
View SolutionIn the given figure, AB//EF//CD. Given that AB = 7.5 cm, EG = 2-5 cm, GC = 5 cm and DC = 9 cm. Calculate :

AC.
View SolutionIn the given figure, AB//EF//CD. Given that AB = 7.5 cm, EG = 2-5 cm, GC = 5 cm and DC = 9 cm. Calculate :

EF
View SolutionIn the given figure, AP = 8 cm, BP = 22 cm, AQ = 12 cm and QC = 8 cm

Show that ΔAPQ is similar to ΔACB.
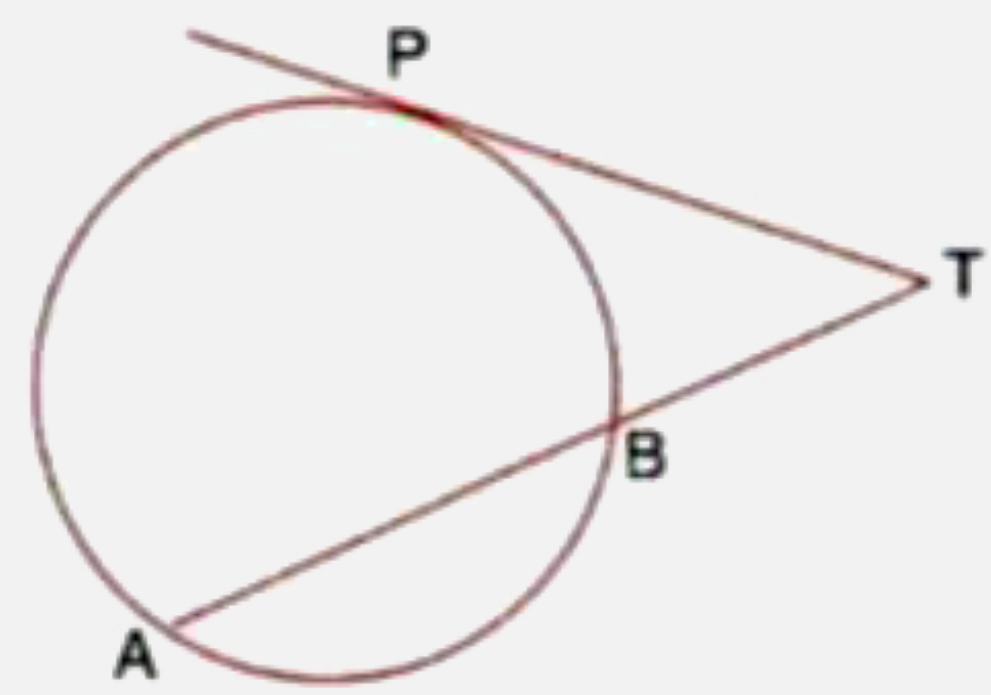
View SolutionIn the given figure find TP if AT=16 cm and AB=12 cm.
View Solution
