M is the mid-point of a line segment AB, AXB and MYB are equilateral triangles on opposite sides of AB, XY cuts AB at Z. Prove that: AZ= 2ZB.
To prove that AZ=2ZB, we will follow a step-by-step approach.
Step 1: Understand the Given Information
We are given:
- M is the midpoint of line segment AB.
- △AXB and △MYB are equilateral triangles on opposite sides of AB.
- Line XY intersects AB at point Z.
Step 2: Identify Key Properties
Since M is the midpoint of AB, we can write:
AM=MB=AB2
Step 3: Use Properties of Equilateral Triangles
In equilateral triangles AXB and MYB:
- AX=AB=BX
- MY=MB=BY
From the properties of equilateral triangles, we know:
AX=AB=BXandMY=MB=BY
Step 4: Establish Relationships Using Similar Triangles
Triangles BXZ and MYZ are similar because:
- ∠ZBX=60∘ (angle in triangle AXB)
- ∠ZMY=60∘ (angle in triangle MYB)
- ∠BZX=∠MZY (vertically opposite angles)
Thus, we can write:
BZMZ=BXMY
Step 5: Substitute Known Lengths
From the properties of the triangles, we know:
- BX=2MB (since BX=AB and AB=2AM)
- MY=MB
Thus, we can express the ratio as:
ZBMZ=2MBMB=2
This implies:
ZB=2MZ(1)
Step 6: Express AM in Terms of MZ
Since M is the midpoint:
AM=MB
And since MB=MZ+ZB:
MB=MZ+2MZ=3MZ(2)
Step 7: Find AZ
Now, we can express AZ:
AZ=AM+MZ
Substituting from (2):
AZ=3MZ+MZ=4MZ(3)
Step 8: Relate AZ and ZB
From (1) and (3):
AZ=4MZandZB=2MZ
Thus, we can write:
AZ=2×ZB
Conclusion
We have proved that:
AZ=2ZB
We are given:
- M is the midpoint of line segment AB.
- △AXB and △MYB are equilateral triangles on opposite sides of AB.
- Line XY intersects AB at point Z.
Since M is the midpoint of AB, we can write:
AM=MB=AB2
In equilateral triangles AXB and MYB:
- AX=AB=BX
- MY=MB=BY
AX=AB=BXandMY=MB=BY
Triangles BXZ and MYZ are similar because:
- ∠ZBX=60∘ (angle in triangle AXB)
- ∠ZMY=60∘ (angle in triangle MYB)
- ∠BZX=∠MZY (vertically opposite angles)
BZMZ=BXMY
From the properties of the triangles, we know:
- BX=2MB (since BX=AB and AB=2AM)
- MY=MB
ZBMZ=2MBMB=2
ZB=2MZ(1)
Since M is the midpoint:
AM=MB
And since MB=MZ+ZB:
MB=MZ+2MZ=3MZ(2)
Now, we can express AZ:
AZ=AM+MZ
Substituting from (2):
AZ=3MZ+MZ=4MZ(3)
From (1) and (3):
AZ=4MZandZB=2MZ
Thus, we can write:
AZ=2×ZB
We have proved that:
AZ=2ZB
Topper's Solved these Questions
- CHAPTERWISE REVISION EXERCISEBOOK - ICSECHAPTER - CHAPTERWISE REVISION EXERCISEEXERCISE - CHAPTERWISE REVISION EXERCISE (LOCI)
7 Videos
- CHAPTERWISE REVISION EXERCISEBOOK - ICSECHAPTER - CHAPTERWISE REVISION EXERCISEEXERCISE - CHAPTERWISE REVISION EXERCISE (CIRCLES)
9 Videos
- CHAPTERWISE REVISION EXERCISEBOOK - ICSECHAPTER - CHAPTERWISE REVISION EXERCISEEXERCISE - CHAPTERWISE REVISION EXERCISE (EQUATIONS OF STRAIGHT LINES)
12 Videos
- BANKING (RECURRING DEPOSIT ACCOUNTS)BOOK - ICSECHAPTER - BANKING (RECURRING DEPOSIT ACCOUNTS)EXERCISE - QUESTIONS
7 Videos
- CIRCLESBOOK - ICSECHAPTER - CIRCLESEXERCISE - EXERCISE 17( C )
28 Videos
Similar Questions
M is the mid-point of a line segment AB. AXB and MYB are equilateral triangles on opposite sides of AB.XYcuts AB at Z. Find m if AZ=mZB.
View SolutionThe mid - point of line segment AB (shown in the diagram) is (-3, 5), Find the co-ordinates of A and B.
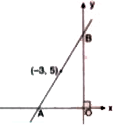 .
.
View SolutionOn the sides AB and AC of triangle ABC, equilateral triangles ABD and ACE are drawn. Prove that :
∠CAD=∠BAE
View SolutionD, E and F are the mid-points of the sides BC, CA and AB respectively of triangle ABC. Prove that:
area of BDEF is half the area of ΔABC.
View SolutionIn the given figure l||m and M is the mid-point of a line segment AB .Show that M is also the mid- point of any line segment CD, having its end points on l and m, respectively.
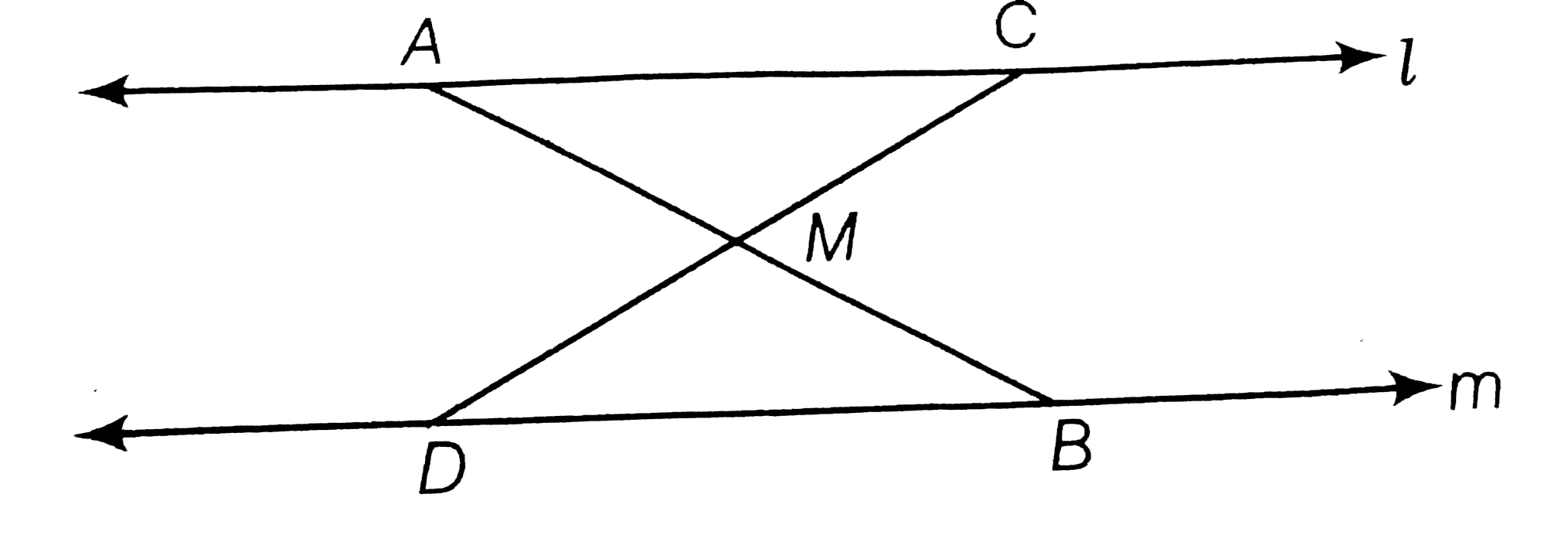
View SolutionD, E and F are the mid-points of the sides AB, BC and CA of an isosceles triangle ABC in which AB = BC. Prove that ΔDEF is also isosceles.
View SolutionD and F are the mid-points of sides AB and AC of a triangle ABC. A line through F and parallel to AB meets BC at point E.
Prove that BDFE is a parallelogram
View SolutionIn triangle ABC, D and E are mid-points of the sides AB and AC respectively. Through E, a straight line is drawn parallel to AB to meet BC at F. Prove that BDEF is a parallelogram. If AB = 16 cm, AC = 12 cm and BC = 18 cm, find the perimeter of the parallelogram BDEF.
View SolutionP (-3, 2) is the mid point of line segment AB as shown in the given figure. Find the P (-3,2) co-ordinates of points A and B.
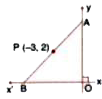
View SolutionAB is a line-segment. P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B. Show that the line PQ is the perpendicular bisector of AB
View Solution
