In the given figure, ∠ABC=90∘ and BC is diameter of the given circle. Show that:
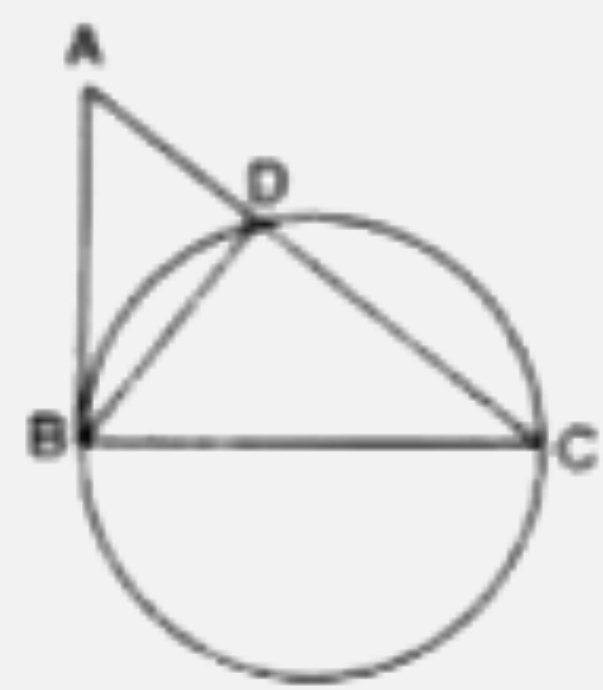
AC×CD=BC2
Step by step video & image solution for In the given figure, angleABC= 90^(@) and BC is diameter of the given circle. Show that: AC xx CD = BC^(2) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CHAPTERWISE REVISION EXERCISEBOOK - ICSECHAPTER - CHAPTERWISE REVISION EXERCISEEXERCISE - CHAPTERWISE REVISION EXERCISE (CONSTRUCTION)
3 Videos
- CHAPTERWISE REVISION EXERCISEBOOK - ICSECHAPTER - CHAPTERWISE REVISION EXERCISEEXERCISE - CHAPTERWISE REVISION EXERCISE (MENSURATION)
8 Videos
- CHAPTERWISE REVISION EXERCISEBOOK - ICSECHAPTER - CHAPTERWISE REVISION EXERCISEEXERCISE - CHAPTERWISE REVISION EXERCISE (CIRCLES)
9 Videos
- BANKING (RECURRING DEPOSIT ACCOUNTS)BOOK - ICSECHAPTER - BANKING (RECURRING DEPOSIT ACCOUNTS)EXERCISE - QUESTIONS
7 Videos
- CIRCLESBOOK - ICSECHAPTER - CIRCLESEXERCISE - EXERCISE 17( C )
28 Videos
Similar Questions
In the given figure, ∠ABC=90∘ and BC is diameter of the given circle. Show that:

AC×AD=AB2
View SolutionIn the given figure if ∠B=90∘ and BD is perpendicular to AC then
prove that:
(i)△ADB~△BDC(ii)△ADB~△ABC
(iii) △BDC~△ABC(iv)BD2=AD×DC
(v) AB2=AD×AC(vi)BC2=CD×AC
(vii) AB2+BC2=AC2

View SolutionIn the given figure AC = BD, prove that AB = CD.

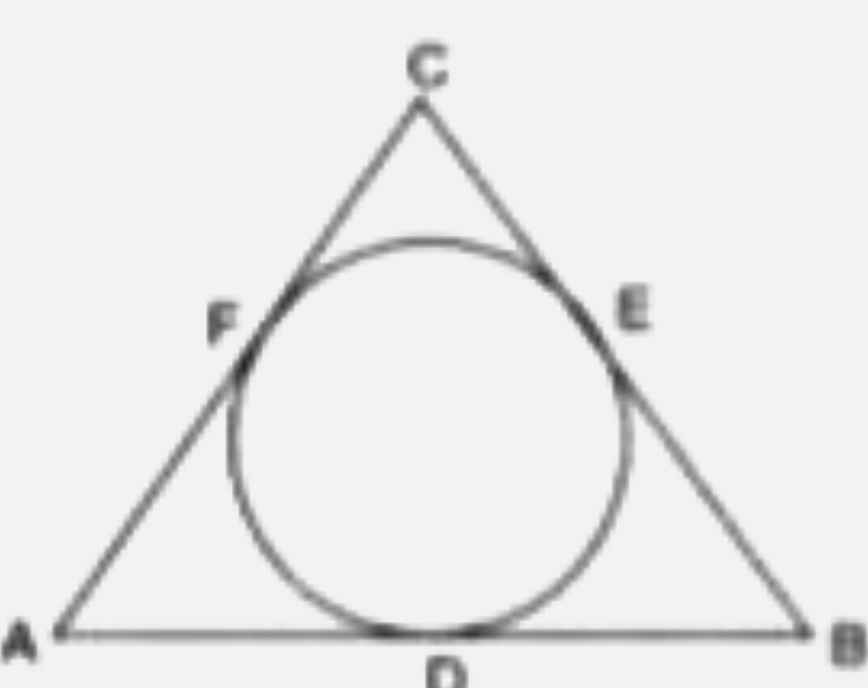
View SolutionIn the given figure, AB, BC and CA are tangents to the given circle. If AB= 12cm, BC= 8cm and AC= 10cm, find the length of AD,BE=CF
View SolutionIn the given figure, AB||CDandBC||AD. Find the values of x, y and z

View Solutionin the given figure ∠CAB=90∘andAD⊥BC. if AC= 75 cm , AB= 1m and BD= 1.25 m . Find AD.

View SolutionIn the given figure, AB∣∣CD. The line segments BC and AD intersect at O. Show that : z=x+y.

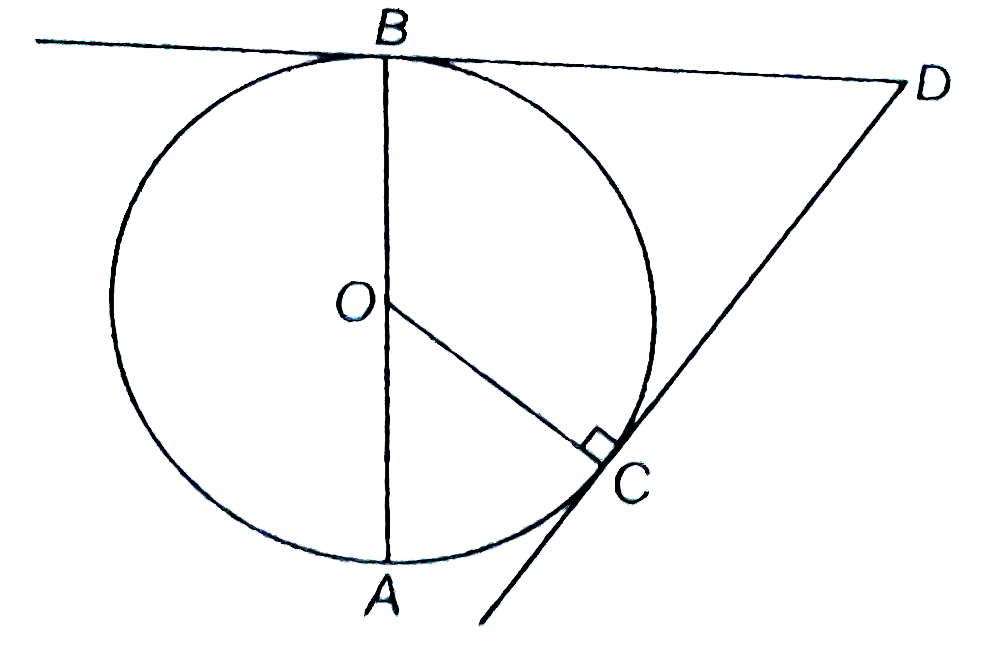
View SolutionIn the given figure, AB is the diameter of the circle, centered at O. If ∠COA=60∘,AB=2r,Ac=dandCD=l, then l is equal to
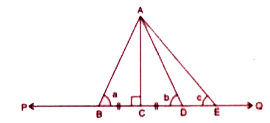
View SolutionIn the given figure, AC is perpendicular to line PQ and BC = CD. Show that AE is greater than AB.
View SolutionIn the given figure, triangle ABC is a right triangle with ∠B=90∘andD is mid-point of side BC. Prove that :
AC2=AD2+3CD2

View Solution
