AB and CD are two chords of a circle intersecting at a point P outside the circle. If
PA= 8cm, PC= 5cm and PD= 4cm, determine AB.
The correct Answer is:5.5cm
To solve the problem, we will use the intersecting chords theorem, which states that if two chords intersect, the products of the lengths of the segments of each chord are equal.
1. Identify the segments of the chords:
- Let PA=8cm
- Let PC=5cm
- Let PD=4cm
- Let AB=xcm
- Therefore, PB=PA−AB=8−xcm
2. Apply the intersecting chords theorem:
According to the theorem, we have:
PA×PB=PC×PD
Substituting the known values:
8×(8−x)=5×4
3. Calculate the right side:
5×4=20
So the equation becomes:
8×(8−x)=20
4. Expand the left side:
64−8x=20
5. Rearrange the equation:
Subtract 64 from both sides:
−8x=20−64
−8x=−44
6. Solve for x:
Divide both sides by -8:
x=−44−8=5.5cm
7. Conclusion:
The length of chord AB is 5.5cm.
- Let PA=8cm
- Let PC=5cm
- Let PD=4cm
- Let AB=xcm
- Therefore, PB=PA−AB=8−xcm
According to the theorem, we have:
PA×PB=PC×PD
Substituting the known values:
8×(8−x)=5×4
5×4=20
So the equation becomes:
8×(8−x)=20
64−8x=20
Subtract 64 from both sides:
−8x=20−64
−8x=−44
Divide both sides by -8:
x=−44−8=5.5cm
The length of chord AB is 5.5cm.
Topper's Solved these Questions
- CHAPTERWISE REVISION EXERCISEBOOK - ICSECHAPTER - CHAPTERWISE REVISION EXERCISEEXERCISE - CHAPTERWISE REVISION EXERCISE (CONSTRUCTION)
3 Videos
- CHAPTERWISE REVISION EXERCISEBOOK - ICSECHAPTER - CHAPTERWISE REVISION EXERCISEEXERCISE - CHAPTERWISE REVISION EXERCISE (MENSURATION)
8 Videos
- CHAPTERWISE REVISION EXERCISEBOOK - ICSECHAPTER - CHAPTERWISE REVISION EXERCISEEXERCISE - CHAPTERWISE REVISION EXERCISE (CIRCLES)
9 Videos
- BANKING (RECURRING DEPOSIT ACCOUNTS)BOOK - ICSECHAPTER - BANKING (RECURRING DEPOSIT ACCOUNTS)EXERCISE - QUESTIONS
7 Videos
- CIRCLESBOOK - ICSECHAPTER - CIRCLESEXERCISE - EXERCISE 17( C )
28 Videos
Similar Questions
AB and CD are two chords of a circle intersecting at a point P outside the circle. If
PC=30cm, CD=14cm and PA=24cm, determine AB.
View SolutionAB and CD are two chords of a circle intersecting at a point P inside the circle. If
AB= 24cm, AP= 4cm and PD = 8cm, determine CP
View SolutionAB and CD are two chords of a circle intersecting at a point P inside the circle. If
AP=3cm, PB= 2.5cm and CD= 6.5 cm, determine CP.
View SolutionAB and CD are two chords of a circle intersecting at P. Prove that AP×PB=CP×PD
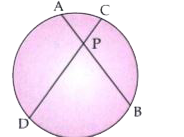
View SolutionIn a circle, chords AB and CD intersect at a point R inside the circle. If AR : RB = 1:4 and CR: RD = 4:9, then the ratio AB: CD is
View SolutionAB and CD are two parallel chords of a circle which are on opposite sides of the centre such that AB=10cm, CD=24cm and the distance between AB and CD is 17cm. Find the radius of the circle.
View SolutionIf chords AB and CD of a circle intersect each other at a point inside the circle, prove that : PA×PB=PC×PD .
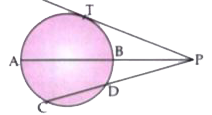
View SolutionIn the figure given below, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD =7.8 cm, PD = 5 cm, PB = 4 cm. Find
(i) AB.
(ii) The length of tangent PT.
View SolutionAB and CD are two parallel chords of a circle on opposite sides of a diameter such that AB = 24 cm and CD = 10 cm. If the radius of the circle is 13 cm, find the distance between the two chords.
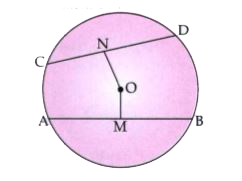
View SolutionIn the figure given below, O is the centre of the circle. AB and CD are two chords of the circle. OM is perpendicular to AB and ON is perpendicular to CD. AB = 24 cm, OM = 5 cm, ON = 12 cm. Find the :
(i) radius of the circle
(ii) length of chord CD
View Solution
