Question

The horizontal distance between two tower is 150 m. The angle of depression of the top of one tower as observed from the top of other tower, which is 120 m in hight, is ${30}^{\circ }.$ Find the height of the first tower.

Explanation

To solve the problem step by step, we will follow the information provided and apply trigonometric principles.

Step 1: Understand the Problem
We have two towers. The height of the second tower (Tower B) is 120 m, and the horizontal distance between the two towers is 150 m. The angle of depression from the top of Tower B to the top of Tower A is 30 degrees. We need to find the height of Tower A.

Step 2: Draw a Diagram
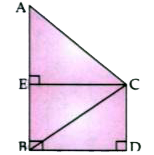
Draw two vertical lines representing the two towers. Label the top of Tower A as point A and the top of Tower B as point B. The ground level between the two towers can be labeled as point C, and the horizontal distance between the two towers can be represented as line segment BC, which is 150 m.

Step 3: Identify the Angles and Heights
From point B (top of Tower B), the angle of depression to point A (top of Tower A) is 30 degrees. The height of Tower B (AB) is 120 m.

Step 4: Use Trigonometry
In triangle ABE, where:
- AB = height of Tower B = 120 m
- BC = horizontal distance = 150 m
- Angle of depression = 30 degrees

We can use the tangent function, which relates the angle of depression to the opposite side (height difference) and the adjacent side (horizontal distance).

Step 5: Set Up the Equation
Using the tangent of the angle of depression:
\( \tan(30^\circ) = \frac{AE}{ED} \)
Where:
- \(AE\) is the height difference between the two towers.
- \(ED\) is the horizontal distance (150 m).

Step 6: Substitute Known Values
We know that:
\( \tan(30^\circ) = \frac{1}{\sqrt{3}} \)
So, we can write:
\( \frac{1}{\sqrt{3}} = \frac{AE}{150} \)

Step 7: Solve for AE
Rearranging the equation gives:
\( AE = 150 \cdot \frac{1}{\sqrt{3}} = \frac{150}{\sqrt{3}} = 50\sqrt{3} \text{ m} \)

Step 8: Calculate the Height of Tower A
The height of Tower A (DC) can be found using:
\( DC = AB - AE \)
Substituting the known values:
\( DC = 120 - 50\sqrt{3} \)

Final Answer
The height of the first tower (Tower A) is:
\( DC = 120 - 50\sqrt{3} \text{ m} \)